Для определения дисперсии

Табл.5

№ заво да	Стоимость основных фондов, Y1 (млн. грн.)	Стоимость выпущенной продукции, Х1 (млн. грн)	Среднегодовая численность персонала, Z1 (чел)
Y1	Y1ср	(Y1-Y1ср)^2	X1	X1ср	(X1-X1ср)^2	Z1	Z1ср	(Z1-Z1сp)^2
	5,0	3.83	1,376711	6,0	7.78	3,1684		130.1	718,24
	3,7	0,016044	7,45	0,1444		331,24
	3,5	0,106711	9,1	1,7424		1036,84
	3,3	0,277378	8,3	0,2704		3,24
	3,9	0,005378	7,7	0,0064		139,24
	3,7	0,016044	8,1	0,1024		0,64
	4,8	0,947378	8,9	1,2544		585,64
	3,6	0,051378	6,8	0,9604		17,64
	4,5	0,453378	7,9	0,0144		852,64
	3,4	0,182044	8,6	0,6724		1211,04
	4,1	0,074711	6,3	2,1904		739,84
	3,5	0,106711	7,6	0,0324		392,04
	3,4	0,182044	9,3	2,3104		249,64
	3,4	0,182044	7,2	0,3364		1011,24
	3,6	0,051378	7,45	0,0784		67,24
∑	4,029333	∑	13,284	∑	7356,4

Тогда дисперсии признаков:

Стоимости основных фондов, Y1 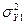=4,029/15=0,2686

Стоимости выпущенной продукции, Х1 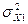=13,284/15=0,8856

Среднегодовой численности персонала, Z1 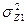=7356,4/15=490,4267

Дисперсия показывает среднюю меру квадратов отклонений значений признаков от средней (классическая мера рассеяния показателей в совокупности)

Замечание: дисперсию также можно получить с помощью функции «=ДИСП(массив)». Получено значение дисперсии с помощью встроенной функции будет кое-что большим, так как в MS Excel дисперсия рассчитывается как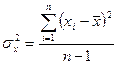

Среднее квадратичное отклонение (СКО): - рассчитывается как квадратный корень из дисперсии, то есть

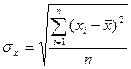
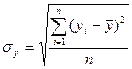
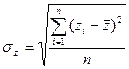
Данные для расчета можно взять из табл..5

Тогда СКО признаков:

Стоимости основных фондов, Y1 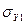==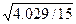0,5183

Стоимости выпущенной продукции, Х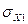1 ==0,9411

Среднегодовой численности персонала, Z1 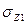==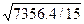22,1456

Содержание среднего квадратичного отклонения аналогично дисперсии.

Замечание: среднее квадратичное отклонение также можно получить с помощью функции «=СТАНДОТКЛОН(массив)». Получено значение дисперсии с помощью встроенной функции будет кое-что большим из тех же причин, что и дисперсия (см. выше).

Проверка нормальности закона распределения показателей в совокупности

Проводится на основе полученных значений абсолютных показателей вариации - размаха вариации, среднего линейного отклонения, дисперсии и середньоквадратичного отклонения. Для нормального закона распределения признаков в совокупность повинную выполняться следующие соотношения между абсолютными показателями вариации:

R=6σ и σ = 1,25d

Для признака Y1 (стоимость основных фондов):

R_Y=1,7млн грн d_Y1=0.422 млн грн 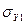=0,5183

6σ_Y1= 6*0.5183=3.110 => 1.7 ≠ 3.11

1.25dY1= 1.25*0.422=0.528 => 0.518 ≠ 0.528.

Так как основные соотношения между абсолютными показателями вариации для признака не выполняются, то распределение совокупности по признаку «стоимость основных фондов» не отвечает нормальному закону.

Для признака Х1 (стоимость выпущенной продукции):

R_х=3,3 млн грн. d_х1=0.765 млн грн 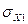=0,9411

6σ_х1= 6*0,9411=5,6466 => 3,3- 5,6466

1.25d_х1= 1.25*0.765=0.9563 => 0.9563 - 0.9411.

Так как основные соотношения между абсолютными показателями вариации для признака не выполняются, то распределение совокупности по признаку «стоимость выпущенной продукции» не отвечает нормальному закону.

Для признака Z1 (среднегодовая численность персонала):

R_Z=67 чел d_Z1=19.12 чел 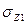=22,1456

6σ_Z1= 6*22.1456=137.537 => 67- 137.537

1.25d_Z1= 1.25*19.12=23.9 => 22.1456 - 23.9.

Так как основные соотношения между абсолютными показателями вариации для признака не выполняются, то распределение совокупности по признаку «среднегодовая численность персонала» не отвечает нормальному закону

2. Относительные показатели вариации признаков:

Коэффициент осцилляции - рассчитывается как отношение размаха вариации к среднему значению признака, то есть:

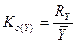
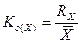
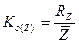
K₀(_Y1) =1.7/3.83*100%=46.83%

K₀(_X1) =3.3/7.78*100%= 42.42%

K₀(_Z1) =67/130.1*100%= 51.46%

Линейный коэффициент вариации- рассчитывается как отношение среднего линейного отклонения к среднему значению признака, то есть:

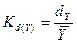
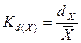
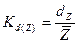
K_d(_Y1) =0,422/3.83*100%=11,63%

K_d(X1) =0,765/7.78*100%= 9,83%

K_d(Z1) =19,12/130.1*100%=14,69 %

Квадратичный коэффициент вариации- рассчитывается как отношение среднего квадратичного отклонения к среднему значению признака, то есть:

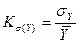
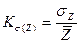
K_σ(_Y1) =0,5183/3.83*100%=14,28%

K_σ(_X1) =0,9411/7.78*100%= 12,10%

K_σ(_Z1) =22,1456/130.1*100%=17,01 %

Коэффициент асимметрии - рассчитывается как отношение разницы между средним значением признака и модой к среднему квадратичному отклонению признака, то есть:

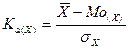
Модальные значения признаков легко найти с помощью функции «=МОДА(массив)» в MS Excel:

Мо_(Y1)=3,4 Мо_(X1)=7,45 Мо_(Z1)=131

K_а(_Y1)=(3,83-3,4)/0,518*100%=82,32%

K_σ(_X1)=(7,78-7,45)/0,941*100%= 35,07%

K_σ(_Z1)=(130,1-131)/22,142*100%=-3,91%

Занесем полученные результаты расчетов к общей таблице показателей вариации:

Дата добавления: 2014-10-22