
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Calculation of certain multiple integrals and Monte Carlo
|
|
|
|
The confidence estimate of the error of simulation calculations
If the goal is to find the expectation MY, you can specify the error of its determination. According to the central limit theorem, for large N, regardless of the distribution of Y:

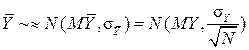 . Hence,
. Hence, 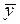
 can not occur further away
can not occur further away
 from the MY, than
from the MY, than 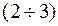 standard deviations:
standard deviations: 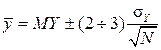 , Equivalent
, Equivalent
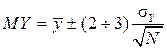 . (14)
. (14)
Here, the factor 2 corresponds to a confidence level of 0.954, and 3 - 0.997.
Example 4. 1 (continued). Replacing the standard deviation of its estimate 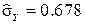 , We obtain:
, We obtain:  with a probability of 0.954.
with a probability of 0.954.
By (14) we can estimate the required number of passes N to achieve the desired accuracy.
Suppose you want to calculate the integral defining g nny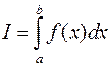 . Recall the mean value theorem.
. Recall the mean value theorem. 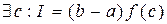 . Point c is unknown. What if we take e f randomly, uniformly distributed on the interval g constant of integration?
. Point c is unknown. What if we take e f randomly, uniformly distributed on the interval g constant of integration?
с → ξ ~ U(a,b). then the result value and the mean value theorem will be random: η = (b - a) f (ξ). What is his expectation?
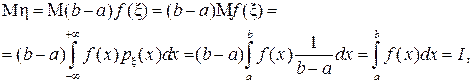
ie coincides with the desired integral!
We know that the expectation of a random variable can be estimated with an accuracy controlled by it generated sample (14), so
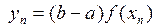 ,
, 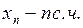 ~ U(a, b); (15)
~ U(a, b); (15)
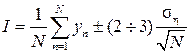 , (16)
, (16)
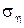 :can be roughly estimated from the top:
:can be roughly estimated from the top: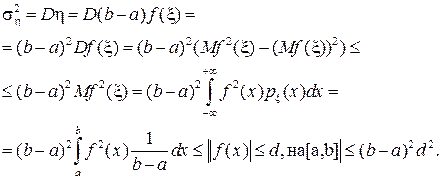
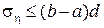 . (17)
. (17)
Or replaced by the estimate of the standard deviation of the sample (15).
Example 4. 2 Calculate the integral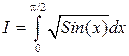 .
.
Use the number t n, a uniformly distributed on [0, 1] from the table of random numbers. Of these, we obtain x n ~ U (0, π / 2).
| n | ||||||||||
| tn | 0.1 | 0.09 | 0.73 | 0.25 | 0.33 | 0.76 | 0.52 | 0.01 | 0.35 | 0.86 |
| xn | 0.157 | 0.141 | 1.147 | 0.393 | 0.518 | 1.194 | 0.817 | 0.016 | 0.55 | 1.351 |
| yn | 0.621 | 0.59 | 1.5 | 0.972 | 1.106 | 1.515 | 1.341 | 0.197 | 1.135 | 1.552 |
According to the formula (16)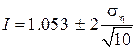 with a confidence level of 0.954. By (17)
with a confidence level of 0.954. By (17) 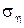 <= 1.57. In this example, we can give a more accurate estimate:
<= 1.57. In this example, we can give a more accurate estimate: 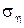 <= 1.253. So I = 1.05 ± 0.79.
<= 1.253. So I = 1.05 ± 0.79.
A summary of the sample  = 0.46, then I = 1.05 ± 0.29.
= 0.46, then I = 1.05 ± 0.29.
Sometimes the error of taking the probable error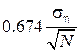 , 0.674 instead
, 0.674 instead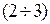 . Its meaning is that the probability that the actual error is greater in absolute value of the error or less identical (= 0.5). Then I = 1.053 ± 0.098
. Its meaning is that the probability that the actual error is greater in absolute value of the error or less identical (= 0.5). Then I = 1.053 ± 0.098
 Если нужно вычислить кратный интеграл
Если нужно вычислить кратный интеграл 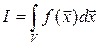 , где V – s – мерный куб, то расчет идёт по формуле (16), где
, где V – s – мерный куб, то расчет идёт по формуле (16), где 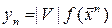 ,
, 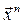 выборка из
выборка из 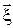 – равномерно распределённого в кубе V случайного вектора;
– равномерно распределённого в кубе V случайного вектора; 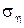 оценивается аналогично.
оценивается аналогично.
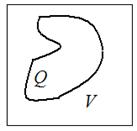
Для вычисления 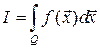 , где Q:
, где Q:
введём 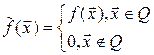 , тогда
, тогда  .
.
Метод Монте-Карло экономнее в вычислениях, чем квадратурные формулы в случае кратных интегралов, и проще учитывает сложную форму области интегрирования Q.
Определение цены опциона методом имитационного моделирования
Опцион на покупку – документ, дающий право, но не обязательство на покупку актива по указанной в нём цене (цена исполнения) в указанную в нём дату (момент исполнения).

Если пренебречь инфляцией, т. е. не рассматривать дисконтирование, то ясно: выгода от обладания опционом на момент исполнения (ценность опциона) – это цена актива на момент исполнения S минус цена исполнения x. Поскольку владелец опциона может отказаться от него без последующих обязательств, ценность опциона не может быть отрицательной:
V = max(S – x, 0).
Цена актива S случайна, значит, и ценность V случайна, и ценой опциона, т. е. тем, что за опцион стоит отдать в момент покупки, надо считать по определению MV – математическое ожидание ценности.
Как образуется S? Будем считать, что цена актива непрерывно наращивается с однодневной ставкой R 1. Значит, через один день цена актива 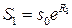 . Для одногодичного опциона (250 торговых дней)
. Для одногодичного опциона (250 торговых дней)  . Для простоты считаем Rt независимыми, одинаково распределёнными величинами.
. Для простоты считаем Rt независимыми, одинаково распределёнными величинами.
Для определения MV с заданной точностью применим имитационное моделирование: нужно получить N «наблюдённых путем проигрывания» модели значений v n, и  . Здесь vn = max (sn – x, 0), и для получения конечной цены актива в n -м прогоне
. Здесь vn = max (sn – x, 0), и для получения конечной цены актива в n -м прогоне 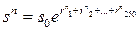 генерируется 250 значений однодневных ставок rnt. При этом используется эмпирическое распределение, построенное по многодневным наблюдениям за однодневной ставкой.
генерируется 250 значений однодневных ставок rnt. При этом используется эмпирическое распределение, построенное по многодневным наблюдениям за однодневной ставкой.
Общие принципы имитационного моделирования многокомпонентных систем
Система – совокупность объектов, объединённых некоторой формой регулярного взаимодействия или взаимозависимости для выполнения заданной функции. Отдельные элементы системы или её подсистемы называются компонентами.
Пример 1. Движение эскадрильи самолётов на учениях. Каждый i -й самолёт – компонента системы, в его движении можно выделить ряд стадий, в ходе которых выполняется последовательность функциональных действий (ФД). При ti 0 начинается взлёт i -го самолёта со взлётной полосы – это функциональное действие ФД i 1. Разгон и боевой разворот – ФД i 2. Стрельба по мишени – ФД i 3 и т. д.

Любое ФД ij выполняется на интервале τ ij и завершается событием С ij. Для каждой i -й компоненты вводится своё локальное время ti.
В имитационной модели ФД ij аппроксимируется некоторым упрощённым функциональным действием (алгоритм АЛ ij), который реализуется при неизменном значении ti, а затем осуществляется изменение ti на τ ij, инициируя появление события С ij. Пара (АЛ ij, τ ij) = АК ij – активность (работа).
Если бы на компьютере имитировалось поведение только одной компоненты, то выполнение активностей можно было бы осуществлять строго последовательно, пересчитывая каждый раз ti. На самом деле компонент много и функционируют они одновременно, а в большинстве компьютеров в каждый конкретный момент может исполняться алгоритм только одной из компонент модели. Необходимо реализовать квазипараллелизм – выстраивание параллельно происходящих активностей в последовательный порядок, с учётом их должной синхронизации (для учёта взаимовлияния). Это делается с помощью глобальной переменной ts – системного времени. Системное время– это мыслимое (в часах, днях, годах) модельное время, в котором происходит эволюция модели. Фактически это последовательность моментов, в которых нужно выполнять какие-либо активности компонент.
Организация квазипараллелизма просмотром активностей
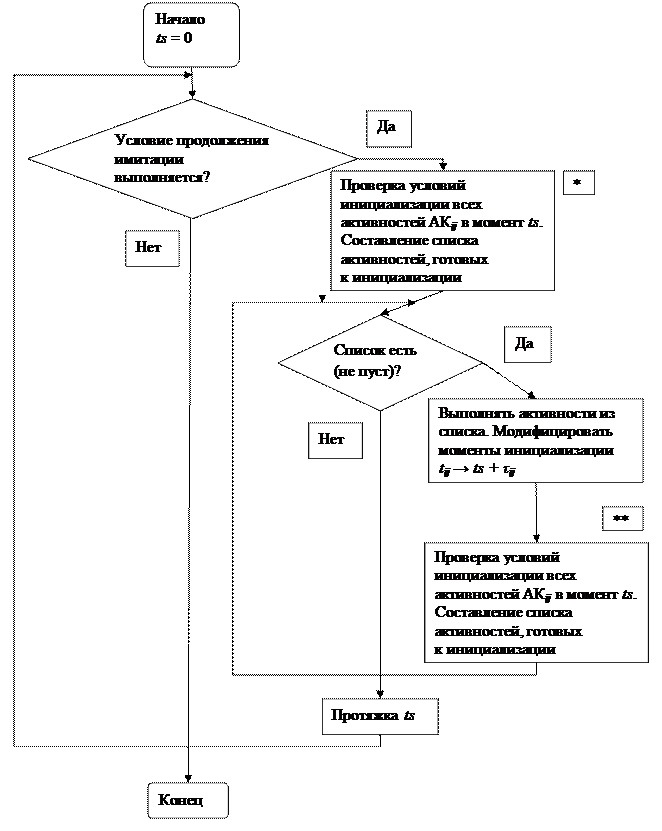 Блок-схема моделирования:
Блок-схема моделирования:
Примечания к схеме:
* – в простейшем случае это проверка по совпадению времени инициализации с ts;
** – новая проверка необходима, т. к. выполнение некоторых активностей может открыть условия инициализации других активностей в тот же момент ts. Например, в момент ts 1-й самолёт готов делать разгон и боевой разворот АК12. 2-й самолёт в принципе готов к взлёту, но пока предыдущий не начал разгона и боевого разворота – нельзя! Поэтому в список * АК21 не попадёт (там будет АК12), а в список ** попадёт. В итоге в ts оба начнут свои действия одновременно, но процессор выполнит их последовательно.
Два способа изменения (протяжки) системного времени
1. До следующего ближайшего события (синхронно-событийный способ):
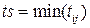 .
.
2. Способ фиксированного шага (синхронно-временной):
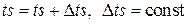 ,
,
и все активности с временами инициализации, попадающими между старым моментом  и новым
и новым 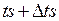 , считаются готовыми к инициализации и как бы одновременными. Их выполнение происходит в неопределённом порядке. Ясно, что при этом могут возникать ошибки моделирования.
, считаются готовыми к инициализации и как бы одновременными. Их выполнение происходит в неопределённом порядке. Ясно, что при этом могут возникать ошибки моделирования.
Пример 2. СМО с одним местом в очереди. АЛ i 1, АЛ i 2 – алгоритм источника: появление заявки, постановка её в очередь или потеря, если места в очереди нет. АЛ k 1 – алгоритм канала обслуживания: готовность принять заявку.
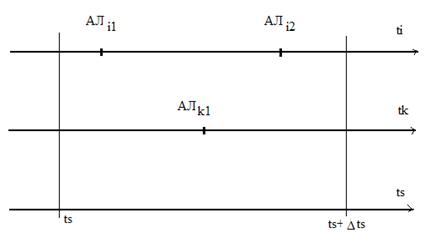
На самом деле потери клиента быть не должно, но если в момент 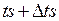 алгоритмы выполнять так: АЛ i 1, АЛ i 2, АЛ k 1, то АЛ i 2 уже вызовет потерю. Поэтому желательно
алгоритмы выполнять так: АЛ i 1, АЛ i 2, АЛ k 1, то АЛ i 2 уже вызовет потерю. Поэтому желательно 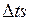 брать поменьше. Синхронно-временной способ применяется, когда события появляются через фиксированные промежутки времени или когда их много и они появляются группами. Во всех остальных случаях применяется синхронно-событийный способ.
брать поменьше. Синхронно-временной способ применяется, когда события появляются через фиксированные промежутки времени или когда их много и они появляются группами. Во всех остальных случаях применяется синхронно-событийный способ.
Пример 5.3. СМО (M | M |1|∞). В таком четырёхпольном обозначении первое поле характеризует распределение интервалов времени между заявками источника (M – экспоненциальное, т. е. это пуассоновский поток); второе поле характеризует распределение времён выполнения заявок каналами обслуживания; третье – число каналов; четвёртое – число мест в очереди.
Пусть интенсивность потока заявок la = 9 заявок/час; интенсивность обслуживаний mu = 12 заявок/час; время моделирования tsmax = 100 час.
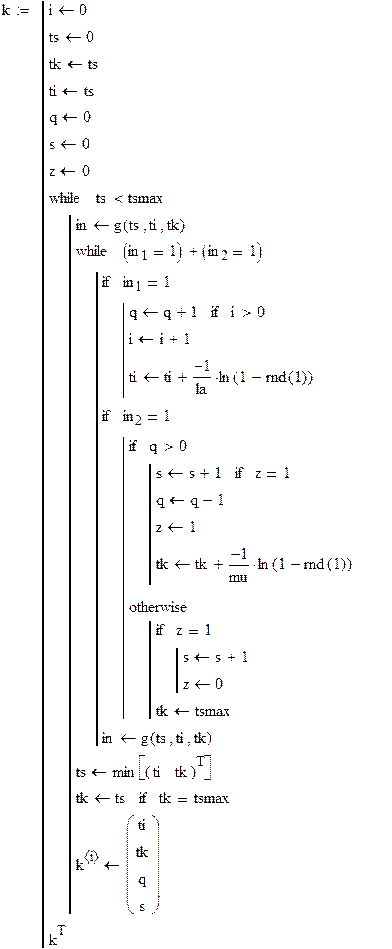 |
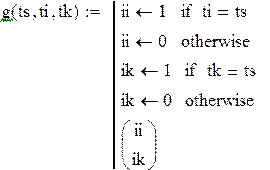
Это подпрограмма проверки условий инициализации активностей и создания списка.
Активность источника. Если это не нулевая заявка (которой фактически не было), то ставит её в очередь, учитывает число заявок, модифицирует своё локальное время появления следующей заявки.
Активность канала. Если очередь не пуста, если канал был занят, то выпуск обслуженной заявки, впуск новой, канал – в состояние «занят», модифицирует своё локальное время окончания обслуживания. Если очередь была пуста, если канал был занят, то выпуск обслуженной, канал – «свободен», время очередной активизации – по активизации источника. Пока его устанавливаем равным tsmax, чтобы не ставить понапрасну в список инициализации в то же время.

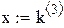

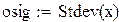

В результате имитации получена оценка средней длины очереди 2.987 заявок. Этот результат будет обсуждаться в разделе 6.4. Оценка стандартного отклонения длины очереди – 3.447 заявок.
Эту программу легко обобщить на моделирование системы (reg | M |1|∞), с регулярным потоком заявок и (M | M| 1|m), с конечным числом мест в очереди, а также на протяжку системного времени синхронно-временным способом.
Организация квазипараллелизма транзактным способом
Этот способ особенно удобен для имитации систем массового обслуживания (СМО). Каждая поступившая заявка (транзакт) образует компоненту системы, для неё устанавливается локальная временная координата  . Активность проявляют здесь не приборы обслуживания (каналы), а сами транзакты, занимая тот или иной свободный прибор и модифицируя свое время следующей инициализации:
. Активность проявляют здесь не приборы обслуживания (каналы), а сами транзакты, занимая тот или иной свободный прибор и модифицируя свое время следующей инициализации: 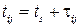 .
.
Существуют специальные языки моделирования транзактным способом, например GPSS (General Purpose System Simulator).
Пример 5.4. Моделирование в GPSS той же системы, что и в примере 5.3.
Barber Storage 1 – описание Barber как 1 параллельно работающий канал.
GENERATE (Exponential (1,0,1/9)) – генерация транзакта через случайный промежуток времени с экспоненциальным распределением, 1 – seed, 0 – сдвиг, 1/9 – среднее время между заявками.
QUEUE Hall запись транзакта в очередь с именем Hall
ENTER Barber вход транзакта в канал
DEPART Hall уход из очереди
ADVANCE (Exponential (1,0,1/12)) задержка в канале (обслуживание)
LEAVE Barber освобождение канала
TERMINATE удаление транзакта
GENERATE 100 моделирование 100 единиц времени
TERMINATE 1 конец моделирования
Написав программу, идём в меню Command → Create Simulation, Command → Start [ Start 1]→ OK.
Отчёт:
START TIME END TIME BLOCKS FACILITIES STORAGES
0.000 100.000 9 0 1
NAME VALUE
BARBER 10000.000
HALL 10001.000
LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY
1 GENERATE 922 0 0
2 QUEUE 922 0 0
3 ENTER 922 0 0
4 DEPART 922 0 0
5 ADVANCE 922 1 0
6 LEAVE 921 0 0
7 TERMINATE 921 0 0
8 GENERATE 1 0 0
9 TERMINATE 1 0 0
QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY
HALL 17 0 922 192 3.133 0.340 0.429 0
STORAGE CAP. REM. MIN. MAX. ENTRIES AVL. AVE.C. UTIL. RETRY DELAY
BARBER 1 0 0 1 922 1 0.813 0.813 0 0
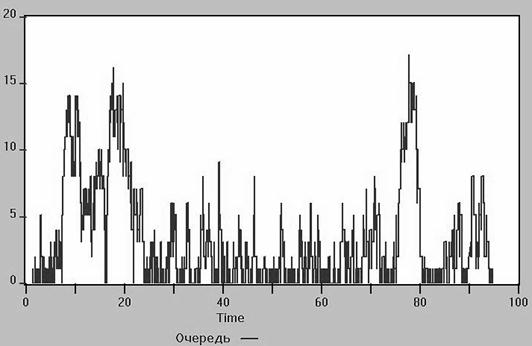
В очередь вошло 922 заявки, максимальное число заявок в очереди 17. Связь между средним числом заявок в очереди 3.133 и средним временем ожидания 0.340, будет обсуждаться в разделе 6.4. Среднее число заявок в канале обслуживания 0.813.
Для получения следующего прогона Command → Reset → Start, если нужно seed сбросить в начальное состояние Command → Retranslate.
Можно добавить вывод графика очереди Window → Simulation Window → Plot Window. Label Очередь, Expression Q$Hall → Plot, Command → Start.
Аналогично – график занятости канала.
Испытание и эксплуатация имитационных моделей
После того как имитационная модель реализована на компьютере и работает, необходимо выполнить следующие этапы.
Верификация и проверка адекватности модели
Верификация
– это проверка соответствия алгоритма функционирования имитационной модели тому замыслу, который был заложен при её разработке. Чаще всего это делается рассмотрением граничных (предельных) случаев (значений параметров), при которых имеется очевидное или дедуктивно найденное решение. Стохастические элементы заменяются на детерминированные и/или вносят другие упрощения.
Проверка адекватности модели
– сравнение имитационной модели с реальной системой, которую она моделирует, т. е. система должна существовать, что бывает не всегда.
Один из способов проверки – сравнение математических ожиданий откликов реальной системы Y * и имитационной модели Y при одинаковых внешних воздействиях, т. е. проверяется гипотеза:
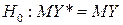
 .
.
Проводится небольшое число M дорогостоящих экспериментов над реальной системой. Получаем выборку: 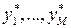 . Проводится большее число N экспериментов над имитационной моделью. Получаем выборку:
. Проводится большее число N экспериментов над имитационной моделью. Получаем выборку: 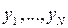 . Вычисляется уровень значимости данных
. Вычисляется уровень значимости данных 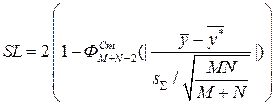 , где
, где  . Подобную проверку необходимо провести для всех фиксируемых откликов.
. Подобную проверку необходимо провести для всех фиксируемых откликов.
Оценка погрешности результирующего показателя имитации из-за различия затравочных чисел генератора псевдослучайных чисел
Генераторы псевдослучайных чисел неидеальны и использование различных «затравочных», seed чисел приводит к различным последовательностям псевдослучайных чисел, а значит и к различным откликам.
Или, если генератор считать вполне случайным, то это разброс отклика из-за случайной природы «первотолчка» (начальных условий работы системы).
В любом случае погрешности результирующего показателя имитации из-за различия seed можно оценить, проведя M перезапусков имитации при различных seed.
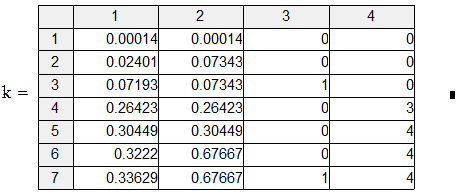
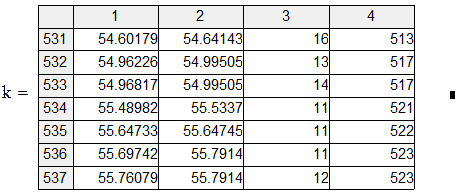
Пример 7.1. Пусть res – вектор-выборка результирующего показателя имитационного моделирования result. Получена при различных seed при прочих равных условиях. 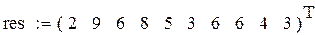
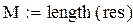
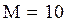
 – оценка математического ожидания по выборке
– оценка математического ожидания по выборке
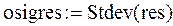 – оценка стандартного отклонения по выборке
– оценка стандартного отклонения по выборке
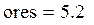

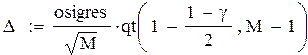 – полуширина доверительногоинтервала с доверительной вероятностью γ для результата моделирования, случайного из-за разных seed. Здесь qt(p, N) – квантиль порядка p распределения Стьюдента с N степенями свободы, поэтому, при γ = 0.95
– полуширина доверительногоинтервала с доверительной вероятностью γ для результата моделирования, случайного из-за разных seed. Здесь qt(p, N) – квантиль порядка p распределения Стьюдента с N степенями свободы, поэтому, при γ = 0.95
(95 %) доверительный интервал
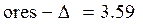 < result <
< result <  .
.
Или, другими словами,  – погрешность и итоговый результат для result:
– погрешность и итоговый результат для result:
result = ores ± Δ = 5.2 ± 1.61.
Методы понижения дисперсии
Антитетический метод
Каждый раз, когда генерируется случайное число r ~ U (0, 1), вычисляется его дополнение (1 – r), которое используется для параллельного определения результата. Значит, если входная переменная довольно велика, в параллельном расчёте она будет довольно мала. Как правило, это ведёт к значениям откликов 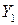 и
и 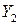 , которые отрицательно коррелированны. Делаем N прогонов, получаем парные результаты:
, которые отрицательно коррелированны. Делаем N прогонов, получаем парные результаты: 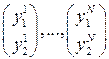 .
.  – выборка из
– выборка из 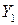 ,
, 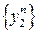 – выборка из
– выборка из 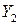 . Ясно, что Y 1 Y 2 распределены одинаково с Y – результат простой (без параллельных расчётов). Введём случайную величину
. Ясно, что Y 1 Y 2 распределены одинаково с Y – результат простой (без параллельных расчётов). Введём случайную величину 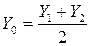 .
.
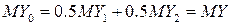 , поэтому MY будем искать так:
, поэтому MY будем искать так:
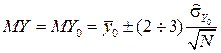 . (24)
. (24)
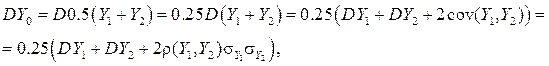
поскольку 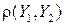 отрицателен, DY 0, будет меньше DY, вплоть до
отрицателен, DY 0, будет меньше DY, вплоть до  при
при 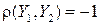 . Значит, работая с Y 0, мы имеем величину с тем же математическим ожиданием, но с уменьшенной дисперсией; поэтому её оценка
. Значит, работая с Y 0, мы имеем величину с тем же математическим ожиданием, но с уменьшенной дисперсией; поэтому её оценка 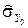 , а значит и погрешность в (24), будет мала.
, а значит и погрешность в (24), будет мала.
Понижение дисперсии при вычислении интегралов
Пусть нужно вычислить интеграл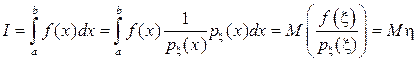 ;
;
здесь – плотность распределения произвольной случайной величины ξ, принимающей значения на (a, b). Дальше рассуждаем, как и прежде:
– плотность распределения произвольной случайной величины ξ, принимающей значения на (a, b). Дальше рассуждаем, как и прежде: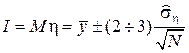 , где
, где 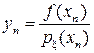 – выборка из η, где xn – выборка из ξ.
– выборка из η, где xn – выборка из ξ.
Выбирая различные распределения  , будем иметь различные
, будем иметь различные 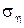 , а значит и погрешности вычисления I. Если взять
, а значит и погрешности вычисления I. Если взять  (считаем f(x) > 0), то
(считаем f(x) > 0), то 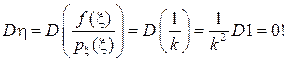 Коэффициент k надо находить из условия нормировки:
Коэффициент k надо находить из условия нормировки:  , что дает
, что дает  ; но входящий сюда интеграл и есть неизвестный нам искомый интеграл! Поэтому практически берут
; но входящий сюда интеграл и есть неизвестный нам искомый интеграл! Поэтому практически берут сходной с
сходной с 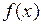 , но так, чтобы с нормировкой всё было просто и генерация
, но так, чтобы с нормировкой всё было просто и генерация 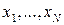 из этого распределения
из этого распределения была бы несложной; статистически оценённая
была бы несложной; статистически оценённая 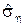 будет малой.
будет малой.
Применение имитационного моделирования (ИМ) к сравнению методов оценивания и анализу их точности
Для решения разнообразных задач (например, эконометрики) исследователи предлагают всё новые и новые модели и методы. Подчас проанализировать аналитически (дедуктивно) характеристики точности и прогностической силы этих методов бывает затруднительно. И здесь приходит на помощь ИМ.
Пример 8.1. Требуется найти оценку функции регрессии yr = β0 + β1 x. Данные (наблюдения) имеют вид: Yn = β0 + β1 xn + En, где En – случайная ошибка (особенность) n -го наблюдения. Будем считать En i. i. d. N (0, so).
Допустим, эксперимент активный, т. е. значения xn фактора исследователи могут выбирать сами.
Пусть есть два исследователя. Оба собираются оценивать вектор коэффициентов регрессии по методу наименьших квадратов (МНК):
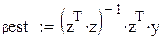 , (25)
, (25)
где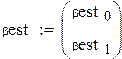 ,
, 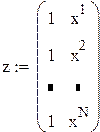 ,
,  .
.
Первый исследователь считает, что значения xn фактора (матрицу плана z) можно выбирать произвольно, второй же высказал догадку, что значения xn лучше брать ортогонально к столбцу из единиц, т. е. 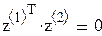 , или
, или  , что, якобы, даст «более точные» оценки
, что, якобы, даст «более точные» оценки 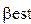 .
.
Как проверить, чей метод лучше?
Идея ИМ: закладываются известные истинные параметры β0 и β1, генерируются N ошибок, одинаковых для обоих методов, и по формуле Yn = β0 + β1 xn + En рассчитываются для каждого исследователя результирующие значения  ,
, 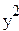 ,...,
,..., по N значениям фактора, выбранным у них по-разному. Затем по этим двум наборам оцениваются
по N значениям фактора, выбранным у них по-разному. Затем по этим двум наборам оцениваются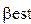 по (25), и видно, что даёт более близкие к истине оценки (лучше)!
по (25), и видно, что даёт более близкие к истине оценки (лучше)!
Чтобы «набрать статистику», проведём М прогонов:
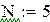
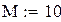 – число прогонов,
– число прогонов, 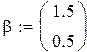
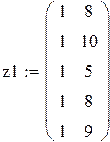 ,
, 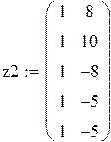
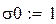
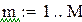
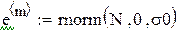

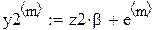
В каждом прогоне оцениваются параметры по N «наблюдениям»:

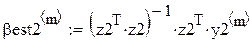
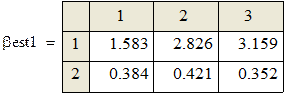

Поскольку каждый прогон даёт независимую реализацию случайной величины Best, то среднее по всем прогонам даёт несмещённую и состоятельную (по M) оценку математического ожидания Best, а Stdev () даёт состоятельную и асимптотически несмещённую оценку стандартного отклонения Best. В частности, для оценки углового коэффициента (который, как мы знаем β1 = 0.5):
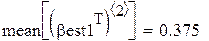
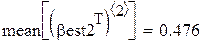
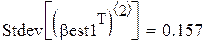
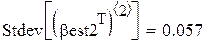
Видно, что второй метод даёт более близкие к истине (0.5) результаты (с меньшим рассеиванием). На этом сравнение данных, якобы теоретически не исследованных методов, можно считать законченным.
Зная теорию, теперь можно её подтвердить:
1. Увеличивая M, убеждаемся, что математическое ожидание оценки коэффициента в обоих методах равно 0.5, т. е. они дают несмещённые оценки.
2. Увеличивая M, убеждаемся, что s оценки коэффициента примерно =  и
и 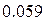 (найдены при M = 1000).
(найдены при M = 1000).
Теория даёт:

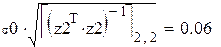
что эквивалентно в последнем случае: 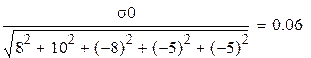
Основная литература
1. Емельянов А. А. Имитационное моделирование экономических процессов: учеб. пособие для студентов, обучающихся по специальности «Прикладная информатика» / А. А. Емельянов, Е. А. Власова, Р. В. Дума; под ред.
2. А. А. Емельянова. – М.: Финансы и статистика, 2004.
3. Лоу А. М. Имитационное моделирование / А. М. Лоу, В. Д. Кельтон; перевод с англ. А. Куленко под ред. В. Томашевского. – 3-е изд. – М.; СПб.; Нижний Новгород [и др.]: Питер, 2004.
4. Советов Б. Я. Моделирование систем: учеб. для вузов / Б. Я. Советов,
5. С. А. Яковлев. – 3-е изд., перераб. и доп. – М.: Высш. шк., 2001.
Дополнительная литература
1. Максимей И. В. Имитационное моделирование на ЭВМ / И. В. Максимей. – М.: Радио и связь, 1988.
2. Лукасевич И. Я. Анализ финансовых операций / И. Я. Лукасевич. – М.: ЮНИТИ, 1998.
3. Ивченко Г. И. Математическая статистика / Г. И. Ивченко, Ю. И. Медведев. – М.: Высш. шк., 1984.
4. Большев Л. Н. Таблицы математической статистики /Л. Н. Большев,
5. Н. В. Смирнов. – М.: Наука, 1983.
6. Исследование операций в экономике / ред. Кремер Н. Ш. / М.: ЮНИТИ, 1997.
7. Айвазян С. А. Прикладная статистика и основы эконометрики /
8. С. А. Айвазян, В. С. Мхитарян. – М.: ЮНИТИ, 1998.
9. Харин Ю. С. Основы имитационного и статистического моделирования /
10. Ю. С. Харин, В. И. Малюгин, В. П. Кирлица и др. – Минск: Дизайн ПРО, 1997.
11. Уотшем Т. Дж. Количественные методы в финансах / Т. Дж. Уотшем,
12. К. Паррамоу. – М.: ЮНИТИ, 1999.
13. Плис А. И. Mathcad 2000. Математический практикум для экономистов и инженеров: учеб. пособие / А. И. Плис, Н. А. Сливина.– М.: Финансы и статистика, 2000.
14. Клейнен Дж. Статистические методы в имитационном моделировании:
15. в 2 т. [пер. с англ.]. / Дж. Клейнен. – Серия: Математико-статистические методы за рубежом. – М.: Статистика, 1978.
16. Коршунов Ю. М. Математические основы кибернетики / Ю. М. Коршунов. – М.: Энергоатомиздат, 1987.
17. Справочник по прикладной статистике: в 2 т. / Ред. Э. Ллойд, У. Ледерман. – М.: Финансы и статистика, 1990.
18. Соболь И. М. Метод Монте-Карло / И. М. Соболь. – М.: Наука, 1972.
19. Кофман А. Займёмся исследованием операций / А. Кофман, Р. Фор. – М.: Мир, 1966.
20. Чистяков В. П. Курс теории вероятностей / В. П. Чистяков. – М.: Наука, 1982.
21. Пакет программ GPSS. Режим доступа:
22. http:// www. minutemansoftware. com / downloads / student. exe
23. Кудрявцев Е. М. GPSS World. Основы имитационного моделирования различных систем / Е. М. Кудрявцев. – М.: ДМК Пресс, 2004.
24. Бородачёв С. М. Элементы математической статистики. Режим доступа: http://study.ustu.ru/view/aid_view.aspx?AidId=372
Лекция 5-9. Эконометрическое моделирование
Обобщенная линейная модель множественной регрессии
Основные этапы моделирования:
1. Идентификация системы. Формулируем цель исследования (анализ, прогнозирование, имитация развития, управленческое решение и т. д.), определяем экономические переменные модели. Анализируем изучаемое явление: формируем и формализуем информацию, известную до начала моделирования. Определяем вид экономической модели, выражаем в математической форме взаимосвязь между переменными, формулируем исходные предпосылки и ограничения модели. Собираем необходимую статистическую информацию
2. Идентификация модели. Проводим статистический анализ модели, оцениваем качество ее параметров
3. Оценка модели. Проверяем истинность модели, определяем, насколько соответствует построенная модель реальному процессу. Построение оцененной модели.
При моделировании многих реальных систем условия КЛЛМР нарушаются.
Пример: 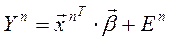 ,
,
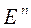 – особенность n -го наблюдения,
– особенность n -го наблюдения,  – номер наблюдения.
– номер наблюдения.
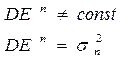 – гетероскедастичность ошибок
– гетероскедастичность ошибок 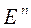 . Например, дисперсия особенностей может зависеть от масштаба объектов, то есть от значений факторов
. Например, дисперсия особенностей может зависеть от масштаба объектов, то есть от значений факторов  :
:

Пример: если используются временные выборки (не пространственные):
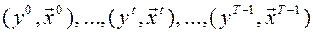 , то часто особенности
, то часто особенности 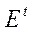 в соседние моменты коррелированны.
в соседние моменты коррелированны.
Определение: ОЛММР –
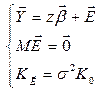 (1)
(1)
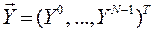 ;
;
 ;
;
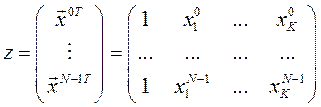 – матрица плана;
– матрица плана;
 – некоторая симметричная невырожденная матрица (предполагается известной):
– некоторая симметричная невырожденная матрица (предполагается известной):
- на диагонали –  ;
;
- вне диагонали – ненулевые ковариации ошибок.
Предположения по выбору 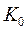 :
:
1. Линейная модель с гетероскедастичными ошибками:
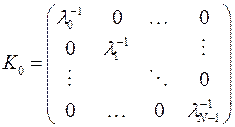
2. Линейная модель с автокоррелированными ошибками:
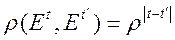 (коэффициенты корреляции соседних ошибок)
(коэффициенты корреляции соседних ошибок)

Замечание: обычные МНК-оценки (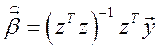 ) остаются несмещенными и состоятельными и для ОЛММР, но неэффективными, то есть существуют лучшие, полученные с помощью ОМНК; обычная МНК-оценка дисперсии ошибок (
) остаются несмещенными и состоятельными и для ОЛММР, но неэффективными, то есть существуют лучшие, полученные с помощью ОМНК; обычная МНК-оценка дисперсии ошибок (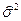 ) оказывается смещенной (заниженной), то есть дающей ложнооптимистичные выводы для стандартных ошибок оценок коэффициентов регрессии.
) оказывается смещенной (заниженной), то есть дающей ложнооптимистичные выводы для стандартных ошибок оценок коэффициентов регрессии.
Обобщенный МНК
Необходимо найти 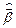 и
и 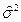 по заданным z и
по заданным z и 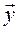 .
.
Сведем ОЛММР к КЛММР.
Известно, что всякая симметричная невырожденная матрица A допускает представление
 , где C – некоторая невырожденная матрица. Разложим
, где C – некоторая невырожденная матрица. Разложим
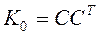 .
.
Умножим (1) слева на C -1: 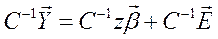 . Переобозначим
. Переобозначим
 .
.
Минимизируя 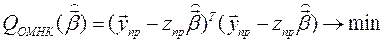 ,(1*)
,(1*)
как и ранее, имеем: 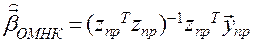 и, возвращаясь к исходным наблюдениям:
и, возвращаясь к исходным наблюдениям:
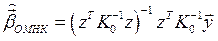 . (1**)
. (1**)
Убедимся, что как и в КЛММР:
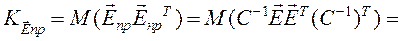
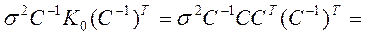
 , поэтому ковариационная матрица оценок коэффициентов регрессии по ОМНК:
, поэтому ковариационная матрица оценок коэффициентов регрессии по ОМНК:
 .
.
Несмещённая оценка коэффициента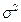 :
:
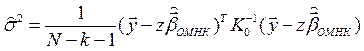 .
.
Коэффициент детерминации:
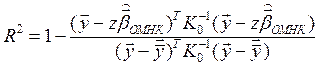 , теперь не обязательно
, теперь не обязательно  , имеет вспомогательное, эвристическое значение.
, имеет вспомогательное, эвристическое значение.
Замечание: подставляя в исходный критерий (1*)
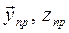 , получим критерий
, получим критерий
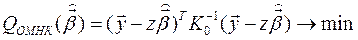 (2)
(2)
через исходные данные ОЛММР. Решение знаем: (1**).
Замечание: ситуации, когда  известна, крайне редки (
известна, крайне редки (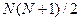 неизвестных параметров).
неизвестных параметров).
В практически реализуемом ОМНК приходится вводить априорные ограничения на структуру матрицы 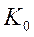 (см. предположения):
(см. предположения):
1) гетероскедастичные ошибки.
Подставляя 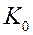 в (2), получим
в (2), получим
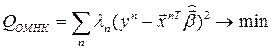 . (3)
. (3)
Поэтому ОМНК в этом случае называют взвешенным МНК ( – веса).
– веса).
Из (3) следует, что на выработку 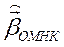 более сильное влияние оказывают данные с меньшей дисперсией ошибок.
более сильное влияние оказывают данные с меньшей дисперсией ошибок.
Замечание: проверка гипотезы о гомо-/гетероскедастичности ошибок:
 (гомоскедастичность);
(гомоскедастичность);
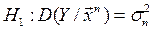 (гетероскедастичность).
(гетероскедастичность).
Разбить выборку {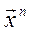 } на G кластеров (g = 1,..., G) (кластер-анализ).
} на G кластеров (g = 1,..., G) (кластер-анализ).
В каждом кластере найти выборочные дисперсии:
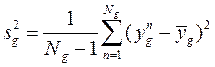 ,
,
где  .
.
Затем для проверки гипотезы 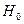 применяется критерий Бартлетта равенства G дисперсий.
применяется критерий Бартлетта равенства G дисперсий.
Если 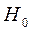 отвергается, то используем ОМНК:
отвергается, то используем ОМНК:
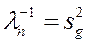 , где g – номер кластера, к которому принадлежит n.
, где g – номер кластера, к которому принадлежит n.
2) автокоррелированные ошибки.
Это могут быть, например, ошибки, связанные моделью авторегрессии 1-го порядка (AR(1)):
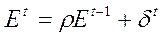 ,
,
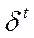 – белый шум:
– белый шум:
 ,
,
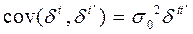 ,
,
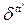 – символ Кронекера.
– символ Кронекера.
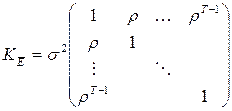 (автокорреляции затухают с увеличением лага),
(автокорреляции затухают с увеличением лага),
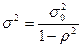 .
.
Замечание: проверка гипотезы о наличии/отсутствии автокорреляции ошибок (критерий Дербина – Уотсона):
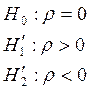
 .
.
Статистика критерия: 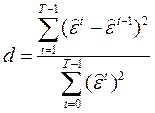 ,
, 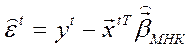 –остатки обычного МНК.
–остатки обычного МНК.
Ясно, что при 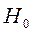
 , поэтому, если:
, поэтому, если:
1) 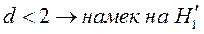 ;
;
2) 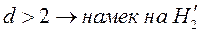 .
.
Таким образом,
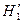 ?
? 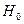
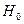 ?
? 
 | | | | |
| | | | |
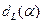
 2
2 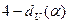
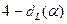 .
.
Если автокорреляция существует, а 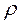 неизвестен, то можно:
неизвестен, то можно:
а) грубо считать, что 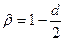 (и подставить это в
(и подставить это в 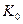 );
);
б) использовать процедуру Кохрейна – Оркатта:
– найти  ;
;
–  ;
;
– оценка 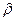 находится как МНК–оценка коэффициента регрессии в модели
находится как МНК–оценка коэффициента регрессии в модели 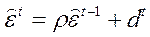 ;
;
– 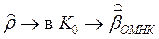 ;
;
– переход к п. 2, где  заменить на
заменить на 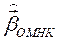 .
.
Продолжаем цикл до тех пор, пока 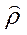 не стабилизируется.
не стабилизируется.
Недостаток алгоритма состоит в том, что есть опасность уйти в локальный минимум  .
.
Прогноз в ОЛММР
Оценка нового yN(T) по известным факторам производится по формулам:
1. Гетероскедастичные ошибки:
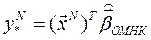 .
.
2. Автокоррелированные ошибки:
 .
.
Дихотомические результирующие показатели. Логит- и пробит-модели
Нередко зависимая переменная – переменная отклика– бинарна по своей природе, т. е. может принимать только два значения. Например, пациент может выздороветь, а может и нет, кандидат на должность может пройти, а может провалить тест при приеме на работу, человек может быть безработным, а может и иметь работу и т. п. Во всех этих случаях нас может заинтересовать поиск зависимости между одной или несколькими “непрерывными” переменными (например, в последнем случае x 1 – возраст, x 2 – доход за последний год, x 3 – стаж работы и т. п.) и одной зависящей от них бинарной переменной.
Конечно, можно использовать стандартную множественную регрессию и вычислить стандартные коэффициенты регрессии. Например, можно задать переменную y со значениями 1’ и 0’, где 1 означает, что соответствующий человек безработен, а 0 – что он занят. Однако здесь возникает проблема: множественная регрессия «не знает», что переменная отклика бинарна по своей природе. Поэтому это неизбежно приведет к модели с предсказываемыми значениями, большими 1 и меньшими 0. Но такие значения вообще не допустимы для первоначальной задачи, таким образом, множественная регрессия просто игнорирует ограничения на диапазон значений для y.
Задача регрессии может быть сформулирована иначе: вместо описания бинарной переменной мы описываем непрерывную переменную со значениями на отрезке [0, 1], которую интерпретируем как вероятность  . (4)
. (4)
Здесь 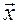 – вектор регрессоров,
– вектор регрессоров, 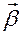 – вектор коэффициентов регрессии.
– вектор коэффициентов регрессии.
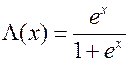 – логистическая функция.
– логистическая функция.
Легко заметить, что вне зависимости от коэффициентов регрессии и значений 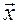 значения p всегда будут принадлежать отрезку [0, 1]:
значения p всегда будут принадлежать отрезку [0, 1]:

Таким образом, модель логит-регрессии имеет вид
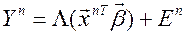 , (5)
, (5)
где En – случайная ошибка в n-м измерении. Очевидно,
En гетероскедастичны, так как их дисперсия зависит от  .
.
Если вместо 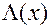 использовать
использовать 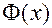 – функцию нормального стандартного распределения, то это будет пробит-модель.
– функцию нормального стандартного распределения, то это будет пробит-модель.
Модель (5) нелинейна по параметрам 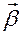 , и перед применением МНК ее следует линеаризовать. Перенесем ошибку налево и применим к обеим частям преобразование, обратное к
, и перед применением МНК ее следует линеаризовать. Перенесем ошибку налево и применим к обеим частям преобразование, обратное к 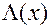 . Ограничиваясь первыми членами разложения левой части по формуле Тейлора, получим:
. Ограничиваясь первыми членами разложения левой части по формуле Тейлора, получим:
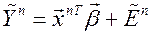 ,
,
где 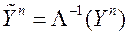 , ошибки гетероскедастичны.
, ошибки гетероскедастичны.
Чтобы при практическом применении МНК последнее выражение имело смысл, необходимо рассматривать группированные или повторяющиеся данные, заменяя  средним значением, не равным 0 и 1.
средним значением, не равным 0 и 1.
Из-за вышеуказанных трудностей оценку вектора коэффициентов регрессии лучше найти методом максимального правдоподобия. Если вероятность получить 1 есть (4), то вероятность получить 0 есть 1- p и вероятность получить цепочку 1, 0, 0, … есть произведение вероятностей p(1-p)(1-p)….
Функция правдоподобия:
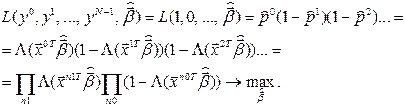
В результате определяется  такой, что вероятность получить при имеющихся факторах имеющиеся отклики будет максимальной. Для проверки качества моделирования (значимости эффектов факторов) проверяется гипотеза
такой, что вероятность получить при имеющихся факторах имеющиеся отклики будет максимальной. Для проверки качества моделирования (значимости эффектов факторов) проверяется гипотеза
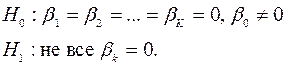
Статистика критерия – логарифм квадрата отношения правдоподобий для моделей H 1 и H 0 – имеет при H 0 приближенно распределение хи-квадрат с K степенями свободы, поэтому уровень значимости:
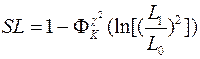 .
.
Маржинальный эффект фактора
Маржинальный эффект фактора xi показывает изменение вероятности
{Y = 1} при изменении фактора xi на единицу.
Можно показать, что он имеет вид:
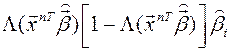 .
.
Пример (продолжение): на сколько процентов увеличится вероятность успеха в задании при увеличении опыта работы (от его среднего значения = 16.88 мес.) на 1 месяц?
Маржинальный эффект = 0.4*0.6*0.161 = 0.038, то есть вероятность успеха повышается на 0.038, или примерно на 10 %.
Стохастические объясняющие переменные
Данная модель имеет вид
 , (6)
, (6)
где теперь  – случайные величины;
– случайные величины;
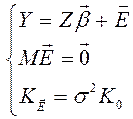
Z – случайная матрица плана.
Рассмотрим три случая.
1. Случайные ошибки 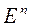 не зависят от
не зависят от 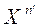 .
.
В этом случае все результаты обычного регрессионного анализа сохраняются. В частности, МНК-оценка остается несмещенной.
Доказательство:
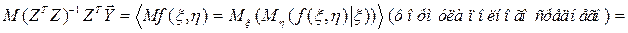
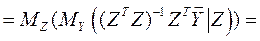
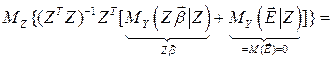
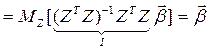 .
.
2. Случайные ошибки зависят от  .
.
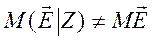 , и оценка
, и оценка 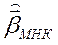 – смещенная и несостоятельная.
– смещенная и несостоятельная.
Метод инструментальных переменных. Пусть существуют некоторые переменные 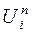 , коррелированные с
, коррелированные с 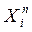 и независимые с
и независимые с  , – «инструментальные переменные»:
, – «инструментальные переменные»:
 ;
;
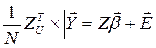 ;
;
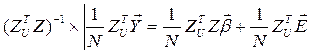 ;
;
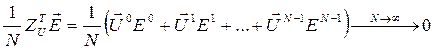 ;
;
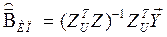 – состоятельная оценка вектора коэффициентов в (6).
– состоятельная оценка вектора коэффициентов в (6).
Замечание: аналогичным способом можно было бы “вывести” и обычную формулу МНК-оценки.
Пример (Модель Кейнса):
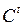 – потребление в стране в
– потребление в стране в 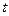 -м году;
-м году;
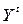 – совокупный выпуск;
– совокупный выпуск;
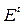 – случайная особенность
– случайная особенность 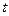 -го года;
-го года;
 – инвестиции.
– инвестиции.
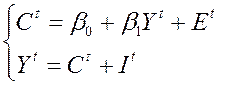 (7, 8)
(7, 8)
(4) –> (5): 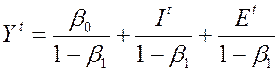 .
.
Видно, что 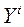 зависит от
зависит от  , поэтому
, поэтому 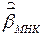 , оцененная по данным уравнения (7), – смещенная и несостоятельная.
, оцененная по данным уравнения (7), – смещенная и несостоятельная.
Возьмем 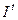 в качестве инструментальной переменной: по (8) она коррелирует с
в качестве инструментальной переменной: по (8) она коррелирует с 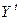 , не зависит от
, не зависит от  , т.к. инвестиции – экзогенная переменная, и определяется другими причинами (может быть, политическими решениями), нежели
, т.к. инвестиции – экзогенная переменная, и определяется другими причинами (может быть, политическими решениями), нежели  :
:
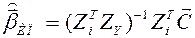 .
.
Пример: измерения неслучайных переменных (факторов) с ошибками (стохастичность – следствие несовершенных измерений):
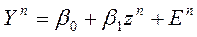 . zn – не случайны, но, измеряя их, мы получаем
. zn – не случайны, но, измеряя их, мы получаем
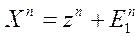 .
. 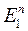 – случайная ошибка измерения;
– случайная ошибка измерения;
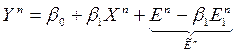 .
.
Поскольку 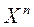 и
и 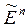 зависят от
зависят от 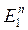 , то они зависимы, а значит, обычные МНК-оценки
, то они зависимы, а значит, обычные МНК-оценки 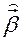 по
по 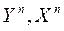 – смещенные и несостоятельные (см. [2], с. 248 – 251; [1], с. 729 – 732).
– смещенные и несостоятельные (см. [2], с. 248 – 251; [1], с. 729 – 732).
3. Объясняющие переменные и случайные ошибки одномоментно некоррелированы (хотя в разные моменты и зависимы).
Пример: 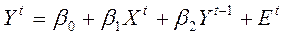 ,
,
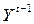 – лаговая объясняющая переменная, ясно, что она зависит от
– лаговая объясняющая переменная, ясно, что она зависит от 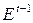 , но не от
, но не от  .
.
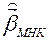 – только асимптотически (в больших выборках) несмещенные.
– только асимптотически (в больших выборках) несмещенные.
Адекватность моделирования. Состоятельные методы
Цели моделирования бывают двух видов:
Прогноз (algoritmic modeling): например, нейронные сети.
Знание механизма (data modeling): 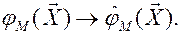
Пример: опасность (несостоятельность) упрощённого data modeling.
Система  ,
,
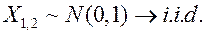
Модель  .
.
По данным  оцениваем
оцениваем 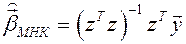 .
.
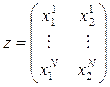 ,
, 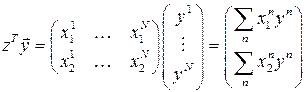 ; (9)
; (9)
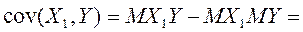
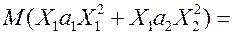

 ;
;
 – несмещенная и состоятельная оценка
– несмещенная и состоятельная оценка 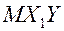 , т.е. ковариации, которая равна 0, значит, (9)
, т.е. ковариации, которая равна 0, значит, (9)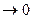 .
.
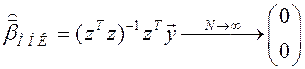 , и может сложиться мнение, что Y вообще не зависит от X1 и X2!
, и может сложиться мнение, что Y вообще не зависит от X1 и X2!
Если проверить гипотезу
 :
:
 , то результат H0 – “да”, т. е. если модель линейна, то β1 может быть равен 0.
, то результат H0 – “да”, т. е. если модель линейна, то β1 может быть равен 0.
 и, казалось бы, оцененная модель
и, казалось бы, оцененная модель 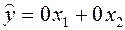 хорошо описывает данные! Оговорка: когда
хорошо описывает данные! Оговорка: когда 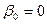 , нельзя гарантировать, что
, нельзя гарантировать, что 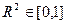 .
.
Таким образом, если не обратить внимания на оговорки, то можно сделать в корне неверные выводы о системе.
Оптимальный предиктор
Пусть  и
и 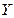 – зависимые случайные величины.
– зависимые случайные величины.
Задача: составить оптимальный прогноз 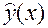 величины Y по известному значению x величины X.
величины Y по известному значению x величины X.
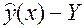 – ошибка прогноза (случайная величина), поэтому точность прогноза целесообразно характеризовать средним квадратом ошибки при данном значении x:
– ошибка прогноза (случайная величина), поэтому точность прогноза целесообразно характеризовать средним квадратом ошибки при данном значении x: