Общие подходы к представлению информации

Лекция 2.

Существует два основных подхода в определении «количества информации»:

1. вероятностный подход — развил американский математик Клод Шеннон
2. объемный подход — возник в результате работы по созданию ЭВМ.

Вероятностный подход

Здесь вводится термин энтропия — количественная мера неопределимости. Теория Шеннона описывалась на фундаментальном понятии энтропии и связанного с ней понятия — количества информации.

При отсутствии неопределенности энтропия = 0, при максимальной неопределенности энтропия должна достигать максимального значение.

Формула Шеннона:

N — число исходов опыта,

i - номер исхода опыта,

P_i — вероятность i -го исхода.

Если исходы опыта равновероятны, то 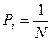(«орел», «решка»).

Ранее в 1928 г. было введено понятие мера Хартии:

,

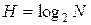данное выражение используется, если события или исходы равновероятны, а ситуацию или результат можно полностью определить после опыта.

Пример: определим количество информации, связанное с появлением каждого символа в сообщениях на русском языке (33 буквы + пробел=N=34):

по (2)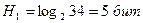

по (1) 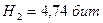- т.к. различные буквы встречаются не одинаково часто.

Пробел: R_i=0,175

О: R_i=0,090

Ф: R_i=0,002 и т.д.

т.о., H₁ — max количество информации, которое приходиться на один знак.

Объемный подход

В техническом устройстве наиболее просто реализовать 2 противоположный физических состояния: намагниченность в двух противоположных направлениях; прибор, пропускающий ток или нет; конденсатор, заряженный или разряженный. Поэтому создатели компьютеров отдают предпочтение двоичной системе счисления (0 и 1 — биты).

Бит — наименьшая единица информации.

Объем информации в двоичных знаках подсчитывается по количеству двоичных символов:

8 бит — 1 байт

1024 байт — 1 кбайт

1024 кбайт — 1 Мбайт

1024 Мбайт — 1 Гбайт

Между вероятностным и объемным количеством информации соотношение неоднозначное. Не всякий тест, записанный двоичными символами, допускает измерение объема информации в кибернетическом смысле, но заведено допускает его в объемном. А если какое-то сообщение можно измерить 2-мя способами, то они не обязательно совпадают, при этом кибернетическое количество информации не может быть больше объемного.

Для самостоятельной работы:

Правовые и этические аспекты информатики:

1. законы РФ по защите информации
2. авторское право
3. имущественные права
4. положительные и отрицательные аспекты этики в развитии информатики

Дата добавления: 2014-10-23