
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные ФОРМУЛЫ, термины и определения. Требования к выполнению контрольной работы
Требования к выполнению контрольной работы
ВВЕДЕНИЕ
Методические указания предназначены для самостоятельной работы студентов-заочников при подготовке к выполнению контрольных работ по курсу математики. Содержат подробное решение примерного варианта контрольной работы № 2 по разделам "Дифференциальное исчисление и интегральное исчисление функции одной переменной", изучаемым в течение второго семестра в курсе математики. Приводятся варианты контрольных работ для студентов заочного отделения. Дается список основных терминов, определений и формул по данным разделам высшей математики. Методические указания будут полезными также студентам первого курса очного отделения при подготовке к контрольным работам и к зачету/экзамену.
Контрольная работа оформляется на листах формата А4 и содержит:
титульный лист (форма приведена в приложении);
основную часть (решение задач);
список использованной литературы.
Оформление решения каждой задачи должно включать в себя: условие задачи, решение с необходимыми пояснениями и комментариями, ответ. Контрольная работа должна быть написана и сдана в сроки, установленные приказом начальника Санкт-Петербургского им. В.Б. Бобкова филиала РТА. Слушатель, не сдавший контрольную работу в срок, считается имеющим академическую задолженность и не допускается к сдаче зачета.
Номер варианта контрольной работы рассчитывается слушателем самостоятельно. Он равен остатку от деления числа, составленного из двух последних цифр номера зачетной книжки, на количество вариантов, и увеличенного на единицу.
Пример 1:
Номер зачетной книжки – 1051 73.
Количество вариантов работ – 10.
Остаток от деления 73 на 10 равен 3 (73/10=7 и 3 в остатке).
Номер варианта контрольной работы (3+1)= 4.
Значит, слушатель должен выполнить контрольную работу "Вариант 4".
Пример 2:
Номер зачетной книжки – 1051 07;
Количество вариантов работ – 10;
Остаток от деления 07 на 10 равен 7 (07/10=0 и 7 в остатке);
Номер варианта контрольной работы (7+1)= 8.
Значит, слушатель должен выполнить контрольную работу "Вариант 8".
Раздел "Дифференциальное исчисление функции одной переменной"
1. Производной функции 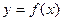 в точке x0 называется предел отношения приращения этой функции к приращению аргумента, при стремлении приращения аргумента к нулю.
в точке x0 называется предел отношения приращения этой функции к приращению аргумента, при стремлении приращения аргумента к нулю.
Обозначения производной: 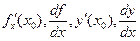 .
.
По определению производной:
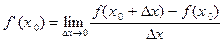 , (1)
, (1)
или, в других обозначениях:
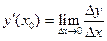 (1)′
(1)′
2. Операция нахождения производной данной функции называется дифференцированием функции. Если существует конечный предел (1), то говорят, что функция дифференцируема в данной точке (имеет производную).
3. Основные правила дифференцирования
Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций т.е.:
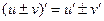 . (2)
. (2)
Производная произведения двух дифференцируемых функций равна произведению производной первой функции на вторую функцию плюс произведение производной второй функции на первую функцию, т.е.:
 (3)
(3)
Следствие 1. Постоянный множитель можно выносить за знак производной, т.е.:
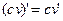 . (4)
. (4)
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на все остальные, т.е.:
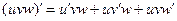 ´ (5)
´ (5)
Производная частного двух дифференцируемых функций определяется формулой:
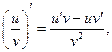 где
где  (6)
(6)
Таблица1.
4. Таблица производных основных элементарных функций
| №п/п | Производная | №п/п | Производная |

| 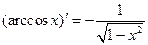
| ||

| 
| ||
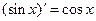
| 
| ||

| 
| ||
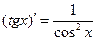
| 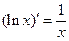
| ||

| 
| ||
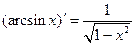
| 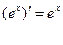
|
5. Сложной функцией называется функция от функции, т.е. функция вида:
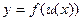 , (7)
, (7)
где  ,
,  ,
,
u промежуточный аргумент, x – независимая переменная.
6. Теорема. Если  и
и  – дифференцируемые функции своих аргументов, то производная сложной функции
– дифференцируемые функции своих аргументов, то производная сложной функции 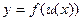 существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т.е.:
существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т.е.:
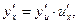 (8)
(8)
6. Производная от первой производной функции  называется второй производной или производной второго порядка и обозначается как
называется второй производной или производной второго порядка и обозначается как  или
или 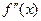 .
.
По определению
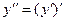 . (9)
. (9)
7. Производной n-ого порядка функции 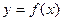 (n -й производной) называется производная от (n – 1) –ой производной:
(n -й производной) называется производная от (n – 1) –ой производной:
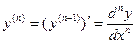 . (10)
. (10)
8. Дифференциалом функции называется главная линейная часть приращения функции  .
.
Обозначение дифференциала – 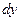 или
или  .
.
По определению
 или
или 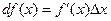 . (11)
. (11)
Можно показать, что  , тогда
, тогда
 . (11)′
. (11)′
Таким образом, дифференциал функции численно равен произведению производной этой функции на дифференциал независимой переменной.
9. Теорема. Если функция 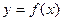 непрерывна на отрезке [a, b] и дифференцируема в интервале (a,b), причем
непрерывна на отрезке [a, b] и дифференцируема в интервале (a,b), причем  (
(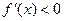 ) для
) для  , то эта функция возрастает (убывает) на отрезке [a, b].
, то эта функция возрастает (убывает) на отрезке [a, b].
Таким образом, знак производной позволяет определить, возрастает или убывает функция в заданном интервале:
если  (функция возрастает); (14)
(функция возрастает); (14)
если (функция убывает). (15)
(функция убывает). (15)
10 Экстремумами называют локальные максимумы и минимумы функции.
11. Теорема. Н еобходимый признак существования экстремума. Если функция 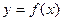 имеет экстремум в точке
имеет экстремум в точке 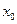 , то ее производная в этой точке равна нулю или не существует.
, то ее производная в этой точке равна нулю или не существует.
12. Точки, в которых производная равна нулю или не существует, называются стационарными (или критическими) точками производной.
13. Теорема. Первый достаточный признак существования экстремума. Если в точке x = x0 производная функции 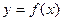 равна нулю и меняет знак при переходе через эту точку, то точка x0 является точкой экстремума, причем:
равна нулю и меняет знак при переходе через эту точку, то точка x0 является точкой экстремума, причем:
x0 – точка максимума, если знак 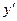 меняется с плюса на минус;
меняется с плюса на минус;
x0 – точка минимума, если знак 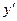 меняется с минуса на плюс.
меняется с минуса на плюс.
14. Теорема. Второй достаточный признак существования экстремума. Если в точке x0 первая производная 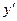 функции
функции 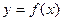 обращается в нуль, а ее вторая производная
обращается в нуль, а ее вторая производная 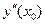 отлична от нуля, то в точке x0 функция
отлична от нуля, то в точке x0 функция 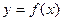 достигает экстремума (минимума, если y¢¢(x0)>0, и максимума, если y¢¢(x0)<0).
достигает экстремума (минимума, если y¢¢(x0)>0, и максимума, если y¢¢(x0)<0).
15. Теорема. Если во всех точках интервала (a, b) вторая производная функции 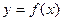 отрицательна (положительна), то кривая
отрицательна (положительна), то кривая 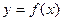 на этом интервале выпукла (вогнута).
на этом интервале выпукла (вогнута).
16. Точка кривой, отделяющая ее выпуклую часть от вогнутой, называется точкой перегиба кривой.
17. Необходимое условие существования точки перегиба. Если кривая 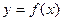 имеет перегиб в точке
имеет перегиб в точке 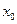 , то вторая производная функции
, то вторая производная функции  в этой точке равна нулю или не существует.
в этой точке равна нулю или не существует.
18. Достаточное условие существования точки перегиба. Если в точке 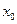 вторая производная
вторая производная  обращается в нуль и меняет знак при переходе через нее, то
обращается в нуль и меняет знак при переходе через нее, то 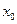 – точка перегиба кривой
– точка перегиба кривой 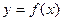 .
.
19. Правило Лопиталя. Если функции 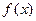 и
и  дифференцируемы в окрестности точки
дифференцируемы в окрестности точки  , обращаются в нуль в этой точке, и существует предел отношения
, обращаются в нуль в этой точке, и существует предел отношения 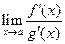 при
при  , то существует и предел отношения самих функций, равный отношению производных, т.е.:
, то существует и предел отношения самих функций, равный отношению производных, т.е.:
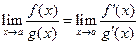 . (16)
. (16)
Замечания:
- правило Лопиталя применяется для раскрытия неопределенностей типа 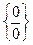 или
или 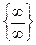 .
.
- правило Лопиталя (16) справедливо и для случая, когда 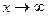 .
.
- правило Лопиталя можно применять повторно, несколько раз.
Раздел "Интегральное исчисление функции одной переменной"
1. Интегрированием называется действие, обратное дифференцированию, т.е. действие, в результате которого находится функция, производная которой равна заданной функции.
2. Функция 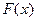 называется первообразной для данной функции
называется первообразной для данной функции 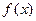 , если для любого x из области определения
, если для любого x из области определения 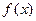 выполняется равенство:
выполняется равенство:
 , (17)
, (17)
или:
 . (18)
. (18)
3. Множество  всех первообразных для данной функции
всех первообразных для данной функции 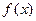 , где С принимает все возможные числовые значения, называется неопределенным интегралом от функции
, где С принимает все возможные числовые значения, называется неопределенным интегралом от функции 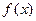 и обозначается символом
и обозначается символом 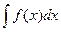 .
.
Таким образом, по определению, неопределенный интеграл есть
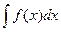 =
=  , (19)
, (19)
где C – произвольная постоянная;
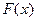 – первообразная для функции
– первообразная для функции 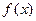 , т.е. функции
, т.е. функции 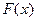 и
и 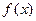 связаны соотношением (17):
связаны соотношением (17):  .
.
4. Основные свойства неопределенного интеграла.
Производная неопределенного интеграла равна подынтегральной функции, т.е.:
 . (20)
. (20)
Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.:
 . (21)
. (21)
Неопределенный интеграл от дифференциала некоторой функции 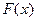 равен самой функции с точностью до произвольной постоянной C, т.е.:
равен самой функции с точностью до произвольной постоянной C, т.е.:
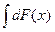 =
=  . (22)
. (22)
Постоянный множитель можно выносить за знак неопределенного интеграла, т.е.:
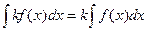 , (k ¹ 0). (23)
, (k ¹ 0). (23)
Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых функций, например, в случае двух функций:
 . (24)
. (24)
Свойство инвариантности:
если 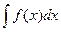 =
=  и
и  ,
,
то:
 =
=  . (24)
. (24)
Таблица 2.
5.Таблица основных интегралов [1]
| № п/п | Интеграл | № п/п | Интеграл |

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 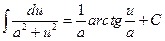
| ||

| 
| ||
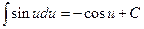
| 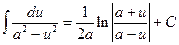
| ||
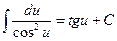
| 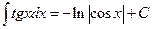
|
6. Формула интегрирования по частям:
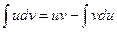 , (25)
, (25)
где  ,
, 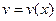 дифференцируемые функции.
дифференцируемые функции.
7. Определенным интегралом от функции 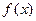 на отрезке [a,b] называется конечный предел ее энной интегральной суммы, когда число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю.
на отрезке [a,b] называется конечный предел ее энной интегральной суммы, когда число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю.
Определенный интеграл обозначают символом 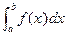 .
.
По определению:
 . (26)
. (26)
где 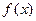 – подынтегральная функция;
– подынтегральная функция;
x – переменная интегрирования;
число 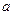 – нижний предел интегрирования;
– нижний предел интегрирования;
число b – верхний предел интегрирования;
 – отрезок интегрирования.
– отрезок интегрирования.
7. Формула Ньютона-Лейбница:
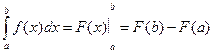 . (27)
. (27)
где: 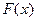 есть какая-либо первообразная для подынтегральной функции
есть какая-либо первообразная для подынтегральной функции 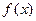 [2].
[2].
8. Формула интегрирования по частям для определенного интеграла:
 . (28)
. (28)
где  ,
, 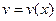 функции, имеющие непрерывные производные на отрезке
функции, имеющие непрерывные производные на отрезке 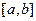 .
.
9. Метод замены переменной (метод подстановки) для вычисления определенного интеграла выражается формулой
 , (29)
, (29)
где: 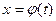 ;
;
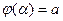 ,
,  .
.
10. Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию y = f(x) и ее производные 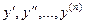 .
.
Символическая запись дифференциального уравнения:
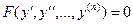 . (30)
. (30)
11. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
12. Общим решением дифференциального уравнения n -го порядка называется функция:
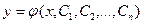 , (31)
, (31)
зависящая от n произвольных постоянных и удовлетворяющая дифференциальному уравнению при любых значениях  .
.
13. Частным решением дифференциального уравнения называется любая функция, полученная из общего решения при конкретных числовых значениях произвольных постоянных:
 . (32)
. (32)
14. Задача отыскания частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям, называется задачей Коши.
15. Теорема Коши (теорема о существовании и единственности решения дифференциального уравнения). Если в уравнении  функция
функция 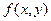 и ее частная производная f¢y непрерывны в некоторой области D, содержащей точку (х0, у0), то существует, и притом единственное, решение этого уравнения
и ее частная производная f¢y непрерывны в некоторой области D, содержащей точку (х0, у0), то существует, и притом единственное, решение этого уравнения  , удовлетворяющее условию:
, удовлетворяющее условию:
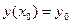 (33)
(33)
Условие (33) есть начальное условие для дифференциального уравнения первого порядка.
Таким образом, теорема Коши утверждает, что существует, и притом единственное, решение задачи Коши.
|
|
Дата добавления: 2014-10-23; Просмотров: 612; Нарушение авторских прав?; Мы поможем в написании вашей работы!