Формат с плавающей точкой

Формат с плавающей точкой предназначен для компактного отображения вещественных чисел в очень широком диапазоне. Число представляется в алгебраическом формате: (S)(F)*2^P, где

· S (Sign) – знак числа. Для положительного S = 0, для отрицательного S = 1.

· F (Fraction) - мантисса (значащая часть).

· P (Power) – порядок.

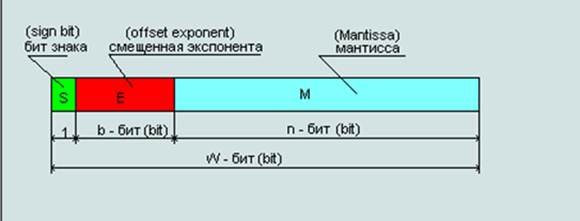
В 1985 институт инженеров по электротехнике и электронике IEEE (Institute of Electrical and Electronics Engineers) в США разработал стандарт представления чисел с плавающей точкой IEEE 754. Согласно этому стандарту слово данных разбивается на три поля.

· Однобитовое поле S (sign - знак) используется для указания знака числа. Для положительного числа S = 0, для отрицательного S = 1.

· Поле F (fraction). В нем записывается дробная часть мантиссы (fraction). Мантисса наряду с дробной частью содержит целую часть (1 или 0). Бит целой части мантиссы в памяти не хранится для уменьшения объема запоминаемых данных, при отображении данных он автоматически учитывается.

· Поле экспоненты (E – exponent), содержит смещённый порядок E=P+Bias. Biass – смещение, выбирается так, чтобы смещённый порядок был положительным или равным нулю.

Если целая часть мантиссы равна единице, то число считается нормализованным, а если она равна нулю, то ненормализованным. Целая часть мантиссы считается равной нулю, только в том случае, когда смещённый порядок числа также равен нулю. Во всех остальных случаях целая часть мантиссы равна единице.

В зависимости от точности представления форма с плавающей точкой имеет 3 стандарта:

· С одинарной точностью SP (Single Precision floating-point format).

· С двойной точностью DP (Double Precision floating-point format).

· С расширенной одинарной точностью формат SEP (Single Extended Precision floating-point format). Это формат для представления результатов промежуточных и конечных вычислений с расширенной одинарной точностью. Применяется для данных, которые не могут быть представлены в формах SP или DP.

Сравнительные данные форм в стандарте IEEE 754:

Параметр	SP	DP	SEP
Длина
Знак числа
Мантисса, всего
Мантисса, дробная часть
Мантисса, целая часть	Неявная 1	Неявная 1	Явная 1
Смещенный порядок E
Смещение Biass
Порядок Pмин	-126	-1022	-1022
Eмин
Порядок Pмакс
Eмакс

Пример. Положительное двоичное число в формате с плавающей точкой SP.

Знак, 1 бит	Смещенный порядок, 8 бит	Мантисса, дробь – 23 бита

Определим десятичный эквивалент этого числа. Количество разрядов смещенного порядка E=8, величина смещения Biass=127. Десятичный эквивалент смещённого порядка равен 2⁶+2⁵+2⁴+2³+2² = 124. Следовательно, порядок P (несмещённый) двоичного числа P=124-127= -3.

Десятичный эквивалент дробной части мантиссы равен 0.5. Так как смещённый порядок больше нуля, то скрытая целая часть мантиссы равна единице. Следовательно, десятичный эквивалент мантиссы равен 1.5. Поскольку знаковый разряд равен нулю, число положительно. Окончательно получим

N₁₀ = 1.5*2^-3 =1.5/8 = 0.1875.

Стандарт IEEE 754 поддерживает представление специальных данных.

Тип	E	Мантисса, дробь	Значение
Нуль	0000 0000	Нуль
Бесконечность	1111 1111	Нуль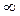
Не число	1111 1111	Не нуль	Не число

Представление двоичных вещественных чисел в форме с ФТ означает, что как для целой, так и дробной части отведено фиксированное число разрядов. То есть местоположение точки, отделяющей целую и дробную части числа, всегда одинаково. Представление двоичных целых чисел в форме с ФТ означает, что точка по существу отсутствует. Достоинством формы с ФТ является простота реализации арифметических операций, а недостатком – ограниченный динамический диапазон. Динамическим диапазоном называют отношение самого большого к самому малому по модулю (но отличным от нуля) чисел, которые можно представить с помощью данной формы. Для формы с ФТ это отношение равно 2^n-1–1.

В общем случае двоичные вещественные числа в форме с ПТ представляются в виде х = m×2^Р, где m – мантисса (вещественное двоичное число со знаком, представленное в форме с ФТ); Р – порядок (целое двоичное число со знаком); 2 – основание двоичной системы счисления. Однако присутствие двух параметров m и Р приводят к неоднозначности представления чисел: одно и то же число можно представить по-разному, например 2 = 2×2⁰ или 2 = 1×2¹ и т.д.

Поэтому и для упрощения арифметики чисел с ПТ применяют нормализованные формы чисел с ПТ. В цифровой технике часто используется нормализованная форма, в которой целая часть мантиссы всегда равна нулю, а первая значащая цифра дробной части отлична от нуля. То есть мантисса ограничена значениями 0,5 £ |m| < 1.

Дата добавления: 2014-10-23