Исходный производящий реечный контур. Основные размеры геометрии зубчатых колёс были даны при условии, что стандартный модуль соответствует их начальным окружностям

Основные размеры геометрии зубчатых колёс были даны при условии, что стандартный модуль соответствует их начальным окружностям, совпадающим с делительными окружностями. Однако это условие налагает ряд ограничений, затрудняющих конструирование зубчатых передач. Это относится к выбору числа зубьев на колесе. Уменьшение числа зубьев удешевляет производство зубчатых колёс, уменьшает размеры передач. Но уменьшение числа зубьев может вызвать их подрез, увеличить износ контактирующих поверхностей. Поэтому, когда необходимо иметь малое число зубьев, проектируют зубчатые колёса с иными размерами.

Меняя отдельные параметры зубчатых колёс: модуль m, коэффициент 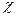высоты головки и ножки зуба, угол зацепления 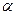и т.д. можно получать зубчатые колёса с различными соотношениями размеров зубьев.

Так как зубчатые колёса получаются методом обкатки, то колёса с требуемыми размерами может быть достигнуто соответствующим расположением нарезаемого колеса (заготовка) по отношению к зуборезному инструменту (рейке).

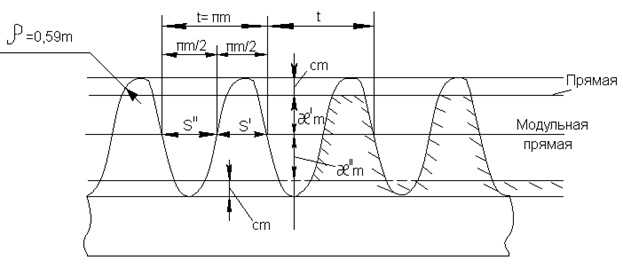
Рис. 5.7. Инструментальная рейка

При нарезании зубчатых колёс методом обкатки с помощью рейки или червячной фрезы в сечении этих инструментов плоскостью, перпендикулярной к оси нарезаемого колеса и содержащей ось червячной фрезы, получаем зубчатую рейку. Размеры зубьев этой рейки, носящей название инструментальной рейки. Обеспечивающее беззазорное зацепление, стандартизованы.

На рис. 5.7. показана инструментальная рейка. Прямая, для которой толщина зуба 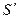равна ширине впадины :

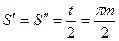(5.19)

называется модульной прямой рейки.

Высота головки и ножки зуба стандартной рейки одинаковы и равны 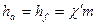. К высоте 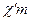добавлена величина, равная . Это необходимо для получения следующей глубины впадины нарезаемого колеса. Обычно глубина впадины равна 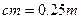, т.е. коэффициент . Переход с прямолинейного участка профиля зуба на прямую головок осуществляется закруглением .

При нарезании стандартного зацепления модульная прямая должна без скольжения перекатываться по начальной окружности нарезаемого колеса, и в этом случае толщина зуба и ширина впадины нарезаемого колеса как из рейки, равны между собой.

Часть рейки, ограниченную высотой головки 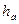, высотой ножки и прямолинейными участками зубьев, будем называть исходным контуром рейки. Этот контур на рис. 5.7 заштрихован. Эвольвентную часть зуба рейки выше исходного контура образует галтель зуба колеса. Далее при образовании профилей зубьев, будем рассматривать только взаимодействие исходного контура рейки с нарезаемым колесом.

При сдвиге рейки эвольвента не изменяется. Если сдвига нет, то колёса носят название нулевых колёс. Если сдвиг рейки направлен в сторону от оси нарезаемого колеса, то колесо называется отрицательным колесом. Если сдвиг направлен в сторону от оси нарезаемого колеса, то колесо называется положительным колесом. Соответственно и сдвигу рейки приписывают отрицательное или положительное значение. Окружность, по которой при обработке колеса перекатывается соответствующая выбранная прямая рейки, носит название начальной окружности обработки или длительной окружности колеса. Начальная окружность обработки колеса может не совпадать с начальной окружностью колеса. При сдвиге рейки диаметр основной окружности не изменяется.

Несовпадение начальной окружности обработки с начальной окружностью колеса не препятствует воспроизведению колёсами требуемого передаточного отношения. Изменение межосевого расстояния не влияет на передаточное отношение , т.к. передаточное отношение представляет собой отношение основных диаметров 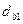и .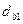

Таким образом, два колеса с эвольвентными профилями зубьев могут быть собраны с различными межосевыми расстояниями. При этом меняются положение полюса зацепления и величина угла зацепления 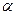. Отсюда следует вывод: для зубчатых колёс эвольвентными профилями зубьев величины радиусов начальных окружностей определяются только после сборки этих колёс. Это позволяет вводить в правильное зацепление два любых колеса, нарезанных одной и той же инструментальной рейкой. Одной из задач при проектировании колёс, является, как избежать подреза зубьев и уменьшить износ путём соответствующего подбора очертания их профилей. Величина абсолютного сдвига в производящей рейке, нарезающей колесо, вычисляется в долях модуля и принимается равной:

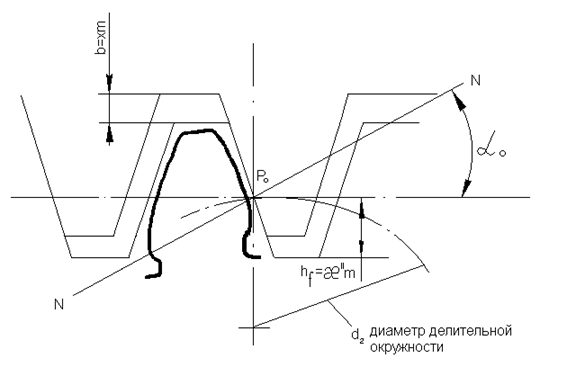
Рис. 5.8. Относительное положение инструментальной рейки при нарезании зубьев колеса со сдвигом.

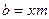(5.20)

где x- коэффициент относительного сдвига или коэффициент сдвига.

Существуют следующие комбинации колёс

1. Нулевая передача, когда оба колеса нарезаны без сдвига или когда одно колесо положительное, а второе отрицательное при равном для обоих колёс коэффициент сдвига 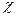, т.е. одно колесо нарезано с положительным сдвигом, а другое – с равным ему по абсолютной величине отрицательным сдвигом (компенсация сдвига)

2. Положительная передача:

а) нулевое колесо с положительным колесом;

б) положительное колесо с отрицательным колесом (при неравных коэффициентах, но при положительной сумме сдвигов).

Все остальные комбинации встречаются редко.

Дата добавления: 2014-10-31