Решение типовых заданий

При решении типовых заданий 1 – 11 необходимо использовать методические пособия [1], [6]–[11], [13], а при решении типовых заданий 12 – 16 – методические пособия [2]–[5], [8]–[13].

1. Найти координаты вектора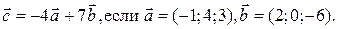

Решение. Используя правила умножения вектора на число и сложения векторов, находим:

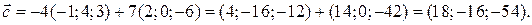
2. Проверить ортогональность векторов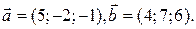

Решение. Два вектора 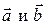называются ортогональными 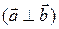, если угол между ними равен 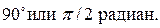Условие ортогональности: скалярное произведение векторов 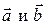равно нулю, 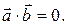Поскольку координаты векторов 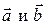заданы в ортонормированном базисе, то скалярное произ-ведение векторов 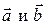вычисляется по формуле: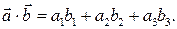

Тогда находим:

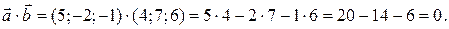
Следовательно,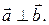

3. Проверить коллинеарность векторов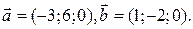

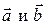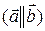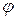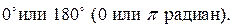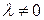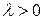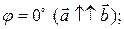Решение. Два вектора называются коллинеарными , если угол между ними равен Условие коллинеарности: существует такое число , что , т.е. координаты векторов пропорциональны, причем при угол при 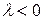,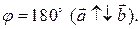Отметим, что векторное произведение векторов 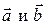равно нулю, . Проверяем условие :

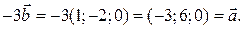Следовательно,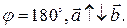

4. Найти площадь параллелограмма, построенного на векторах 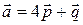и 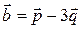, как на сторонах, если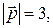

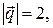
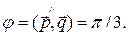
Решение. Площадь параллелограмма выражается через модуль векторного произведения векторов: Используя свойства линейности вектор-ного произведения, находим:

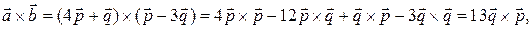
где учли, что

Отсюда, используя определение векторного произведения векторов, получим:

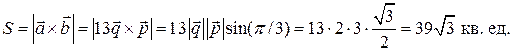
5. Найти площадь параллелограмма, построенного на векторах 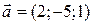и 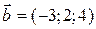, как на сторонах.

Решение. Площадь параллелограмма выражается через модуль векторного произведения векторов: 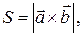где векторное произведение векторов 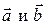вычисляется по формуле:

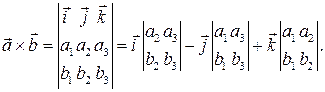
Тогда находим:

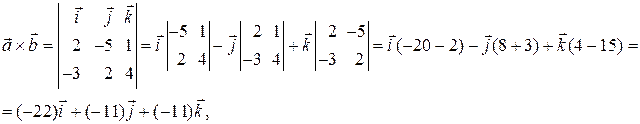
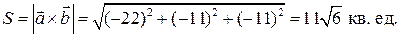
6. Проверить компланарность трех векторов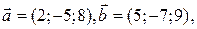

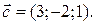
Решение. Три вектора 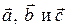называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Условие компланарнос-ти: смешанное произведение векторов 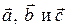равно нулю,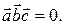

Поскольку координаты векторов 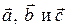заданы в правом ортонормиро-

ванном базисе, то находим:

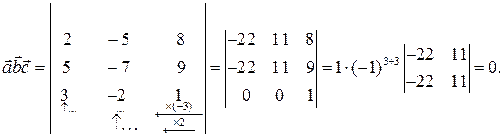
Следовательно, векторы 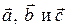– компланарны.

7. Записать каноническое уравнение прямой, проходящей через точки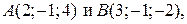

Решение. Каноническое уравнение прямой, проходящей через две точки 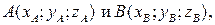имеет вид:

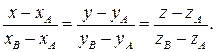
Отсюда находим:

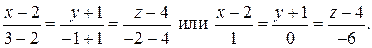
8. Записать уравнение плоскости с заданным вектором нормали 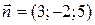, проходящей через точку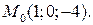

Решение. Уравнение плоскости с заданным вектором нормали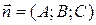, проходящей через точку 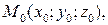имеет вид: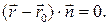

Находим:

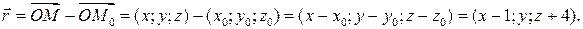Тогда получим:

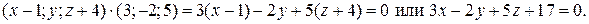
9. Записать уравнение плоскости, проходящей через три точки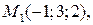

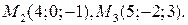
Решение. Уравнение плоскости, проходящей через три точки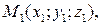

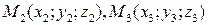, имеет вид: 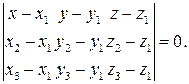Отсюда

находим:

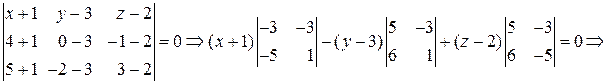
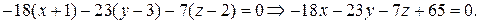
10. Найти значение многочлена 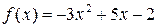от матрицы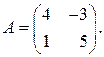

Решение. Запишем искомое значени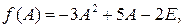е: где 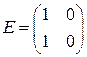– единичная матрица. Используя правила умножения матрицы на матрицу, находим: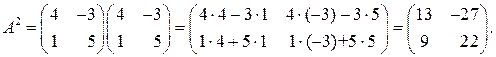

Далее, используя правила умножения матрицы на число и сложения матриц,

получим:

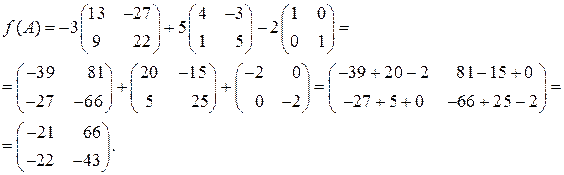
11. Решить систему по формулам Крамера или методом Гаусса, если

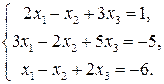
Решение. Вычислим определитель системы:

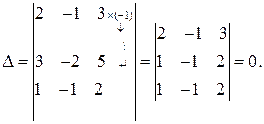
Так как определитель системы равен нулю, то система вырожденная и, следовательно, формулы Крамера применить нельзя. Поэтому данную систему будем решать методом Гаусса. Для этого преобразуем расширенную матрицу системы к трапециевидному виду:

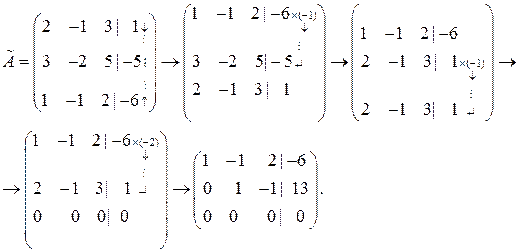
Отсюда следует, что полученной трапециевидной матрице соответствует система

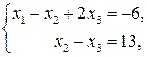
эквивалентная исходной системе, и она совместная (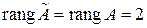) и неопределенная (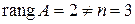), причем базисный минор

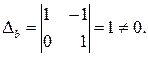Следовательно, 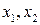– базисные неизвестные, а 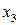– свободная неизвестная. Совершая обратный ход метода Гаусса, находим решения системы:

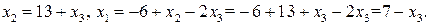
Ответ запишем в виде вектора-решения:

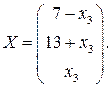
12. Вычислить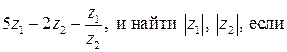

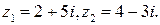
Решение. Используя правила действия над комплексными числами, находим:

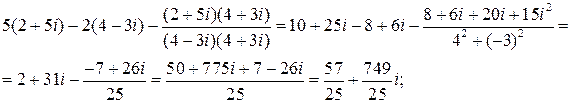
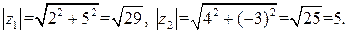
13. Найти производную сложной функции и записать ее дифференциал, если

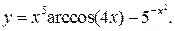
Решение. Используя правила дифференцирования и таблицу производных,

находим:

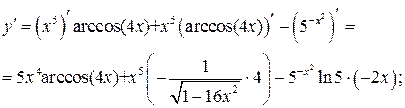
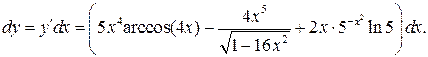
14. Найти производную функции, заданной неявно уравнением

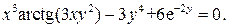
Решение. Используя правила дифференцирования и таблицу производных,

находим:

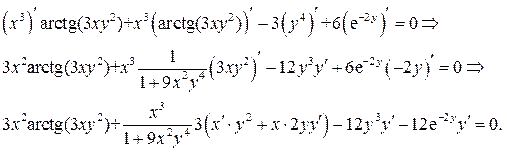
Из последнего равенства выражаем :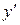

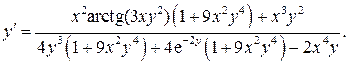
15. Найти производную функции, заданной параметрически системой

уравнений

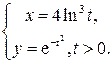
Решение. Запишем производную в дифференциальной форме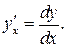

Используя правила дифференцирования и таблицу производных, находим дифференциалы функций:

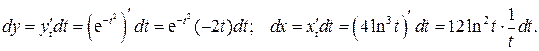
Тогда получим:

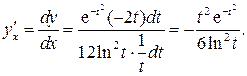
16. С помощью правила Лопиталя вычислить предел

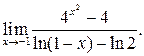
Решение. Используя правило Лопиталя, вычисляем предел:

Литература

Дата добавления: 2014-10-31