Основные элементарные функции и их графики. Пусть функция определена на множестве , а функция на множестве

Сложная функция

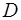Пусть функция определена на множестве , а функция на множестве , причем для соответствующее значение . Тогда на множестве определена функция , которая называется сложной функцией от 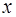(или суперпозицией за­данных функций, или функцией от функции).

Переменную называют промежуточным аргументом сложной функции.

Например, функция есть суперпозиция двух функций и . Сложная функция может иметь несколько промежуточных аргументов.

Основными элементарными функциями называют следующие функции.

1) Показательная функция 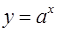, , 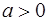. На рис. 4 показаны графики показательных функций, соответствующие различным основани­ям степени.

2) Степенная функция 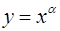, . Примеры графиков степен­ных

функций, соответствующих различным показателям степени, пред­ставлены на рис. 5.

3) Логарифмическая функция , , 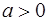; Графики лога­рифмических функций, соответствующие различным основаниям, показа­ны на рис. 6.

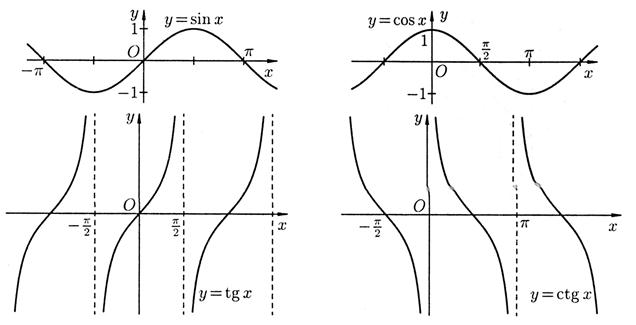
4) Тригонометрические функции ; ; ; . Графики тригонометрических функций имеют вид, показанный на рис. 7.

5) Обратные тригонометрические функции , , , . На рис. 8 показаны графики обратных триго­нометрических функций.

Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и опера­ций взятия функции от функции, называется элементарной функцией.

Примерами элементарных функций могут служить функции

; ; .

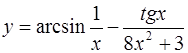Примерами неэлементарных функций могут служить функции

если , если .

Дата добавления: 2014-10-31