Теоретические основы работы

Методом наклонного маятника

Определение коэффициента трения качения

Лабораторная работа № 4

Цель работы

Изучение закономерностей при внешнем трении и экспериментальное измерение коэффициента трения качения для различных материалов.

Во всех механических явлениях имеют место силы трения, действие которых практически всегда связано с переходом механической энергии в тепловую. Силы всемирного тяготения, упругие силы, рассматриваемые в механике, а также силы взаимодействия электрически заряженных тел зависят только от конфигурации тел, то есть от их взаимного расположения, но не от их скоростей. Отличие сил трения от указанных сил состоит в том, что силы трения, помимо конфигурации, зависят от относительной скорости тех тел, между которыми они действуют.

Силы трения могут возникать между соприкасающимися телами или их частями как при их относительном перемещении, так и при их относительном покое.

Внешнее трение действует в плоскости касания двух прижатых друг к другу тел при их относительном движении (например, трение между бруском и наклонной плоскостью, с которой он соскальзывает).

Внутреннее трение проявляется между различными частями одного и того же тела (между различными слоями жидкости или газа).

Трение между поверхностями двух соприкасающихся тел при отсутствии между ними жидкой, газообразной прослойки, называется сухим. Если между твердыми телами имеется тонкий слой жидкости (смазочного масла), то в этом случае трение называется жидкостным.

По кинематическому признаку внешнее трение можно разделить на трение скольжения и трение качения.

Рассмотрим движение (качение) шара (или цилиндра) по горизонтальной поверхности и возникающее при этом движении трение качения.

Для объяснения сил трения качения следует считать деформации шара (цилиндра) и плоскости качения неупругими, причем для простоты будем полагать, что деформируется только поверхность качения, и только она имеет некоторые пластические деформации (в реальных условиях возникают упругие и пластические деформации как шара (цилиндра), так и плоскости).

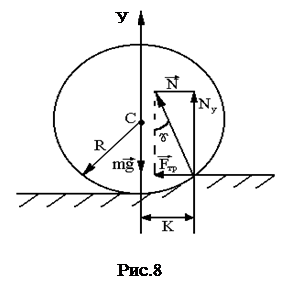
Точка приложения и направление реакции опоры (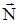), или силы воздействия плоскости на катящийся шар (цилиндр) представлены на рис.8.

Уравнение проекций сил 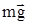и 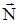на ось У имеет вид:

-mg +N·cosγ=0. (1)

Угол γ практически мал, cosγ» 1, то есть

N»mg. (2)

Горизонтальная составляющая реакции опоры представляет собой силу трения качения .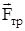

Так как вращение шара (цилиндра) равномерное, и угловое ускорение его равно нулю, то должно выполняться условие равенства моментов* сил, то есть момент силы трения качения относительно точки С равен проекции силы нормального давления N_y, умноженной на К:

F_тр·R=N_у·K, (3)

где R - радиус шара (цилиндра);

N_у = N×cosγ = N;

К - линейная величина, называемая коэффициентом трения качения.

Коэффициент трения качения имеет размерность длины, поэтому он называется также «плечом» силы трения качения шара (цилиндра).

Из равенства (3) с учетом, что N_у»N получаем следующее выражение для силы трения качения:

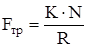. (4)

В данной лабораторной работе предлагается один из способов исследования процесса трения качения - метод наклонного маятника.

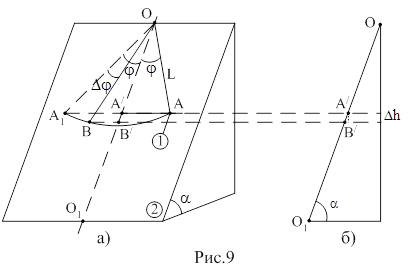
Шарик 1, подвешенный в точке О на нити длиной L, может катиться по наклонной плоскости 2, составляющей регулируемый угол α с горизонтальной поверхностью (рис.9а).

ОО₁ - направление (ось), фиксирующее положение равновесия наклонного маятника, точки А^| и В^| - проекции точек А и В на ось ОО₁.

Идея данного метода заключается в определении связи уменьшения угла φ отклонения нити маятника с коэффициентом трения качения К.

Если маятник отклонить от положения равновесия на угол φ (точка А, рис.9а) и отпустить, то при отсутствии трения шарик 1 через половину периода* оказался бы в точке А₁. Но при наличии трения качения шарик окажется (остановится) в точке В, нить маятника составит угол (φ-Dφ) с осью ОО₁, причем точка В расположена ниже, чем точка А. Это означает, что происходит уменьшение потенциальной энергии маятника (DU), равное работе сил трения качения на пути АВ.

Следует отметить, что работой по преодолению сопротивления среды и трения в подвесе маятника ввиду их малости можно пренебречь.

DU = A_тр,

mgDh = F_трDS, (5)

где m - масса шарика;

Dh - потеря высоты (рис.9б);

DS - длина дуги АВ;

F_тр - сила трения качения, определяемая по формуле (4), в которой сила нормального давления тела (шара) на наклонной плоскости равна

N = mg×cosα. (6)

Из геометрических соображений определим Dh и DS.

Длина дуги АВ равна (рис.9а)

DS = L(2φ-Dφ), (7)

где L - длина нити или радиус дуги АВ окружности.

Изменение высоты Dh определяется как проекция отрезка A^|B^| на вертикальную ось (рис.9,б):

Dh = (A^|B^|)×sina = DL×sina,

где DL = A^|B^| = OB^| - OA^| = L×cos(j - Dj) - L×cosj,

Dh = L×sina[cos(j - Dj) - cosj]. (8)

Подставив в (5) формулы (4), (6), (7) и (8), получим следующее выражение:

mg×L×sina[cos(j - Dj) - cosj] = (K×mg×cosa/R)×L(2j - Dj). (9)

Учитывая, что Dj << 1 (за половину полного колебания потеря угла составляет порядка Dj @ 0,3° = 5,2×10^-3 рад), то можно считать, что

cosDj» 1, sinDj @ Dj

и cos(j - Dj) = cosj×cosDj + sinj×sinDj = cosj + Dj×sinj.

С учетом указанных упрощений выражение (9) можно представить в виде:

.

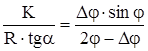Откуда 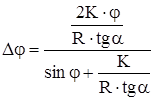. (10)

Так как коэффициент трения качения мал, например, порядка 10^-5 м при движении стали по стали [1], то

sinj >> K/(R×tga),

и при малых углах отклонения шарика от положения равновесия
(j=6°=0,1 (рад))

sinj» j,

тогда уменьшение угла отклонения шарика от положения равновесия за половину полного колебания равно

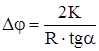. (11)

Тогда за одно полное колебание уменьшение угла отклонения удвоится,
т. е. ,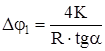

а за n полных колебаний

.

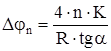Итак, коэффициент трения качения при вышеуказанных упрощениях рассчитывается по формуле:

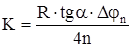или 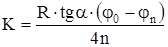, (12)

где Dj_n = (j₀ - j_n) - уменьшение угла отклонения маятника за n колебаний, выраженное в радианах.

Дата добавления: 2014-10-31