
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамика материальной точки. Законы сохранение импульса и энергии. Работа. Мощность 4 страница
|
|
|
|
1. 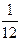 2.
2. 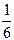 3.
3. 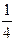 4.
4. 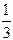 5.
5. 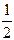
23. Математический маятник длиной 1 м установлен в лифте, опускающемся вниз с ускорением 2,5 м/с2. Период колебания маятника равен … с.
1. 1,6 2. 1,8 3. 2,0 4. 2,3 5. 3,2
24. К пружине подвешен груз массой 10 кг. Если под влиянием силы 9,8 Н пружина растягивается на 1,5 см, то период вертикальных колебаний груза равен…с.
1. 0,78 2. 0,96 3. 1,2 4. 1,8 5. 2,58
25. Спиральная пружина обладает жесткостью k = 25 Н/м. Чтобы за время t = 1 мин совершалось 25 колебаний, к пружине надо подвесить тело массой … кг.
1. 0,001 2. 0,11 3. 1,66 4. 3,65 5. 9,55
26. Дифференциальное уравнение свободных колебаний без затухания имеет вид (ω02, k, m, β, r – постоянные, не равные нулю) …
1.  2.
2. 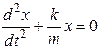 3.
3. 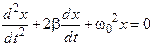
4.  5.
5. 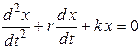
1. 3, 5 2. 1, 4 3. 2, 4 4. 1, 2 5. 1, 2, 4
27. Дифференциальное уравнение свободных затухающих механических колебаний имеет вид …
1. 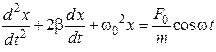 2.
2.  3.
3. 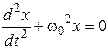
4. 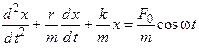 5.
5. 
28. Дифференциальное уравнение вынужденных механических колебаний имеет вид …
1. 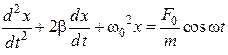 2.
2. 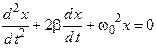 3.
3. 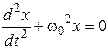
4. 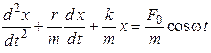 5.
5.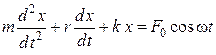
1. 1, 2 2. 2, 4 3. 2, 3, 5 4. 1, 4, 5 5. 3, 4, 5
29. Период колебаний физического маятника равен  . В этой формуле l – это …
. В этой формуле l – это …
1. длина маятника
2. ширина маятника
3. длина оси маятника
4. расстояние от оси до центра масс
5. нет верного ответа
30. Математический маятник длиной L 1 = 40 см и физический маятник в виде тонкого прямого стержня длиной L 2 = 80 см и массой 0,5 кг синхронно колеблются около одной и той же горизонтальной оси. Приведенная длина физического маятника равна … см.
1. 5,44 2. 80 3. 40 4. 32 5. 2,72
31. Обруч диаметром D = 1 м висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Приведенная длина обруча равна … м.
1. 2,0 2. 1,5 3. 1,0 4. 0,5 5. 0,10
32. Однородный тонкий стержень длиной  совершает колебания около горизонтальной оси, проходящей через конец стержня. Приведенная длина маятника равна…
совершает колебания около горизонтальной оси, проходящей через конец стержня. Приведенная длина маятника равна…
1.  2.
2. 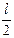 3.
3. 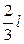 4. l 5.
4. l 5. 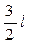
33. Тонкий обруч, подвешенный на гвоздь, вбитый горизонтально в стену, колеблется в плоскости, параллельной стене. Радиус обруча равен 30 см. Период колебаний равен … с.
1. 1 2. 1,1 3. 1,55 4. 1,8 5. 0,3
34. Диск радиуса R колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Период его колебаний равен …
1.  2.
2. 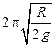 3.
3. 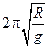 4.
4. 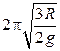 5.
5. 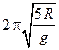
35. Два диска одинакового радиуса и массами 2 и 8 кг соответственно совершают колебания относительно оси, касательной к их поверхности. Периоды колебаний дисков относятся как … (ответ поясните).
1. 1:2 2. 1:1 3. 2:1 4. 1:4 5. 4:1
36. Коэффициент затухания колебаний маятника можно увеличить …
1. уменьшив массу колеблющегося тела
2. уменьшив начальную амплитуду колебания
3. увеличив массу колеблющегося тела
4. увеличив начальную амплитуду колебания
5. уменьшив начальную амплитуду колебаний и вязкость среды
37. Коэффициент затухания – это физическая величина, …
1. показывающая во сколько раз уменьшается амплитуда колебаний за период
2. обратная времени, по истечении которого амплитуда колебаний уменьшается в «е» раз
3. обратная числу колебаний, по завершению которых амплитуда колебаний уменьшается в «е» раз
4. обратная числу колебаний, по завершению которых амплитуда колебаний уменьшается до нуля
5. обратная времени, по истечении которого амплитуда колебаний уменьшается до нуля
38. Шарик радиусом 10 см и массой 0,5 кг, подвешенный к нити длиной 20 см, совершает затухающие колебания в среде с коэффициентом затухания 2 кг·с-1. Коэффициент сопротивления среды равен … с-1.
1. 0,14 2. 1 3. 2 4. 4 5. 8
39. За 10 с амплитуда пружинного маятника массой m = 0,1 кг уменьшилась в е раз. Коэффициент затухания 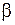 и коэффициент сопротивления среды
и коэффициент сопротивления среды 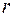 равны …
равны …
1. 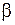 = 1;
= 1; 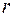 = 0,01 кг·с-1
= 0,01 кг·с-1
2. 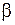 = 0,1;
= 0,1; 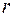 = 0,1 кг·с-1
= 0,1 кг·с-1
3. 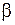 = 0,1;
= 0,1; 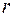 = 0,02 кг·с-1
= 0,02 кг·с-1
4. 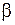 = 0,01;
= 0,01; 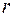 = 0,04 кг·с-1
= 0,04 кг·с-1
5. 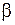 =
= 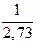 ;
; 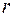 = 0,02 кг·с-1
= 0,02 кг·с-1
40. Период Т затухающих колебаний груза массой m на пружине жесткостью k можно рассчитать по формуле … (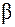 – коэффициент затухания,
– коэффициент затухания, 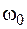 – циклическая частота свободных незатухающих колебаний колебательной системы).
– циклическая частота свободных незатухающих колебаний колебательной системы).
1. 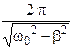 2.
2. 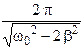 3.
3.  4.
4. 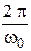 5.
5. 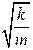
41. За время релаксации амплитуда затухающих колебаний …
1. увеличивается в 2 раза
2. уменьшается в 2 раза
3. увеличивается в e раз
4. уменьшается в e раз
5. не изменяется
42. Если период колебаний 2,5 с, коэффициент затухания 2 с-1, то логарифмический декремент затухания равен ….
1. 0,8 2. 1,25 3. 5 4. 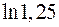 5.
5. 
43. За один период амплитуда колебаний математического маятника с логарифмическим декрементом затухания 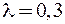 уменьшится в …раз.
уменьшится в …раз.
1. 0,3 2. 0,37 3. 1,35 4. 2,73 5. 3,33
44. Логарифмический декремент затухания – это физическая величина, …
1. показывающая во сколько раз уменьшается амплитуда колебаний за период
2. обратная числу колебаний, по прошествии которых амплитуда колебаний уменьшается до нуля
3. обратная числу колебаний, по прошествии которых амплитуда колебаний уменьшается в «е» раз
4. обратная промежутку времени, за которое амплитуда колебаний уменьшается в «е» раз
5. обратная промежутку времени, за которое амплитуда колебаний уменьшается до нуля
45. Логарифмический декремент затухания колебаний маятника λ. Если амплитуда колебаний уменьшилась в n раз, то маятник совершил … колебаний.
1.  2.
2. 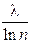 3.
3. 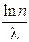 4.
4. 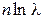 5.
5. 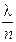
46. Период затухающих колебаний Т = 4 с. Добротность системы Q = 5. Логарифмический декремент затухания λ равен …
1. 20 2. 1,57 3. 1,25 4. 0,80 5. 0,63
47. Период затухающих колебаний Т = 4 с, логарифмический декремент затухания λ = 1,6. Добротность системы (Q) равна …
1. 0,4 2. 0,79 3. 1,96 4. 2,5 5. 6,4
48. При сложении двух одинаково направленных колебаний, описываемых соответственно уравнениями 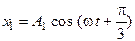 м и
м и  м получается колебание с амплитудой А, равной … м.
м получается колебание с амплитудой А, равной … м.
1. 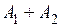 2.
2. 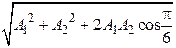 3.
3. 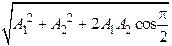
4. 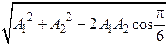 5.
5. 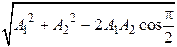
49. Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной …
1. 0 2. 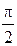 3.
3. 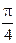 4.
4. 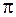 5.
5. 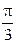
50. При сложении одинаково направленных гармонических колебаний одной частоты с амплитудами 10 см и 6 см, возникло колебание с амплитудой 14 см. Разность фаз складываемых колебаний равна … град.
1. 30 2. 45 3. 60 4. 90 5. 120
51. Складываются два колебания одинакового направления с амплитудами А 1 = 3 см и А 2 = 4 см. Чему равна разность фаз этих колебаний  (в радианах), если амплитуда А результирующего колебания равна 5 см?
(в радианах), если амплитуда А результирующего колебания равна 5 см?
1. 0 2. 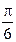 3.
3. 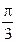 4.
4.  2.
2. 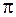
52. Складываются два колебания одинакового направления с амплитудами А 1 = 3 см и А 2 = 4 см. Амплитуда А результирующего колебания равна 6,1 см. Разность фаз складываемых колебаний равна … рад.
1. 0 2. 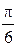 3.
3. 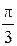 4.
4. 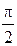 5.
5. 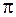
53. Складываются два колебания одинакового направления с амплитудами А 1 = 3 см и А 2 = 4 см и разностью фаз 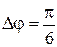 рад. Амплитуда А результирующего колебания равна … см.
рад. Амплитуда А результирующего колебания равна … см.
1. 1,0 2. 6,08 3. 6,77 4. 5,0 5. 7
54. Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами 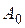 . При разности фаз
. При разности фаз  амплитуда результирующего колебания равна …
амплитуда результирующего колебания равна …
1. 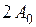 2.
2. 
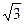 3. 0 4.
3. 0 4. 
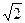 5.
5. 
55. Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами 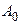 . При разности фаз
. При разности фаз 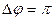 амплитуда результирующего колебания равна …
амплитуда результирующего колебания равна …
1. 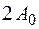 2.
2. 
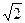 3. 0 4.
3. 0 4. 
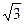 5.
5. 
56. Длина волны, распространяющейся в воздухе, равна 1 м. Разность фаз 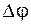 колебаний двух точек, лежащих на луче и отстоящих друг от друга на расстоянии 2 м, равна …
колебаний двух точек, лежащих на луче и отстоящих друг от друга на расстоянии 2 м, равна …
1. 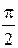 2.
2. 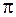 3.
3. 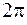 4.
4. 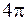 5. 0
5. 0
57. Длина волны, распространяющейся в воздухе, равна 2 м. Разность фаз 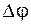 колебаний двух точек, лежащих на луче и отстоящих друг от друга на расстоянии 1 м, равна …
колебаний двух точек, лежащих на луче и отстоящих друг от друга на расстоянии 1 м, равна …
1. 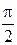 2.
2. 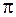 3.
3. 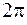 4.
4. 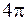 5. 0
5. 0
58. При сложении двух происходящих в одном направлении колебаний, описываемых соответственно уравнениями 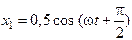 м и
м и 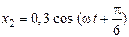 м, получается гармоническое колебание с амплитудой, равной … м.
м, получается гармоническое колебание с амплитудой, равной … м.
1. 0,34 2. 0,44 3. 0,58 4. 0,7 5. 0,8
59. Колебания с частотой 40 Гц распространяются в воздухе со скоростью 400 м/с. Соседние точки пространства, колебания в которых происходят в противофазе, находятся на расстоянии … м.
1. 400 2. 40 3. 20 4. 10 5. 5
60. Если расстояние между точками бегущей волны, распространяющейся в стали равно 2,5 м, а колебания в них отличаются по фазе на 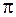 , то частота звуковых колебаний равна … Гц. Скорость звука в стали равна 5 км/с.
, то частота звуковых колебаний равна … Гц. Скорость звука в стали равна 5 км/с.
1. 200 2. 500 3. 1000 4. 2500 3. 5000
61. В результате сложения двух гармонических колебаний одинакового направления с частотами 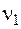 = 1000 Гц и
= 1000 Гц и 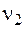 = 1002 Гц получаются колебания с периодически изменяющейся амплитудой (биения). Период биений равен …
= 1002 Гц получаются колебания с периодически изменяющейся амплитудой (биения). Период биений равен …
1. 1 мс 2. 10 мс 3. 50 мс 4. 0,5 с 5. 1 с
62. При сложении двух гармонических колебаний одинакового направления с частотами 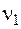 = 1000 Гц и
= 1000 Гц и 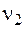 (
(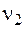 >
>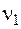 ) получают колебания с периодически изменяющейся амплитудой (биения). Период биений равен 20 мс. Частота второго колебания равна … Гц.
) получают колебания с периодически изменяющейся амплитудой (биения). Период биений равен 20 мс. Частота второго колебания равна … Гц.
1. 998 2. 1005 3. 1020 4. 1050 5.1200
63. В результате сложения двух гармонических колебания одинакового направления получаются колебания с периодически изменяющейся амплитудой (биения). Период биений равен 0,25 с. Разность частот Δν складываемых колебаний равна … Гц.
1. 1 2. 2 3. 2,5 4. 4 5. 8π
64. Уравнение бегущей вдоль оси х плоской гармонической волны имеет вид …
1.  2.
2. 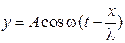 3.
3. 
4. 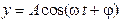 5.
5. 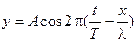
65. Уравнение бегущей вдоль оси х плоской гармонической волны имеет вид …
1.  2.
2. 3.
3.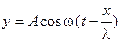
4.  5.
5. 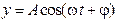
66. Уравнение плоской бегущей вдоль оси х волны имеет вид …
1. 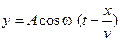 2.
2. 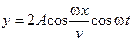 3.
3. 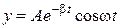
4.  5.
5. 
67. Уравнение плоской бегущей волны имеет вид у = 2 sin (4 t –3 x), м. Длина волны равна…см.
1. 3 2. 75 3. 133 4. 157 5. 209
68. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 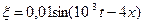 , м. Период колебаний равен … мс.
, м. Период колебаний равен … мс.
1. 4 2. 6,28 3. 1 4. 1000 5. 0,01
69. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид
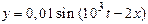 . Волновое число равно … рад/м.
. Волновое число равно … рад/м.
1. 2 2. 10 3. 100 4. 500 5. 1000
70. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид ξ = 0,01sin(103 t - 2 x). Скорость распространения волны равна … м/с.
1. 2 2. 3,14 3. 500 4. 1000 5. 2000
71. Период колебаний Т = 0,12 с. Колебания распространяются со скоростью υ = 300 м/с. Волновое число равно … м –1.
1. 52 2. 36 3. 5,73 4. 0,17 5. 4·10– 4
72. Уравнение стоячей волны имеет вид …
1. 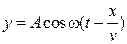 2.
2. 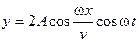 3.
3. 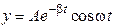
4.  5.
5. 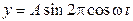
73. Расстояние между соседними узлами стоячей волны, равно 10 м. Длина волны равна … м.
1. 0,05 2. 0,1 3. 0,15 4. 0,2 5. 0,4
74. Расстояние между пучностью и ближайшим к ней узлом стоячей волны равно 20 см. Длина волны равна … м.
1. 0,1 2. 0,2 3. 0,3 4. 0,4 5. 0,8
75. Расстояния между соседними пучностями стоячей волны равно 20 см. Длина волны равна … м.
1. 0,8 2. 0,4 3. 0,2 4. 0,10 5. данных недостаточно
76. Точка участвует в двух взаимно перпендикулярных колебаниях  (м) и
(м) и 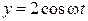 (м). Уравнение траектории результирующего движения точки имеет вид …
(м). Уравнение траектории результирующего движения точки имеет вид …
1. 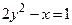 2.
2. 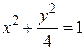 3.
3. 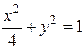 4.
4.  5.
5. 
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 1885; Нарушение авторских прав?; Мы поможем в написании вашей работы!