Логические основы ЭВМ

Позиционные системы счисления.

Совокупность приемов записи и наименования чисел называется системой счисления.

Числа записываются с помощью символов, и по количеству символов, используемых для записи числа, системы счисления подразделяются на позиционные и непозиционные. Если для записи числа используется бесконечное множество символов, то система счисления называется непозиционной. Пример: римская система счисления.

Позиционные системы счисления для записи чисел используют ограниченный набор символов, называемых цифрами, и величина числа зависит не только от набора цифр, но и от того, в какой последовательности записаны цифры, т.е. от позиции, занимаемой цифрой. Пример: десятичная система счисления.

Количество цифр, используемых для записи числа, называется основанием системы счисления и обозначается q. Десятичная система счисления: q=10 {0,1,2,3,4,5,6,7,8,9}. В компьютерах используется двоичная система счисления: q=2 {0,1}. Восьмеричная: q=8 {0,1,2,3,4,5,6,7}. Шестнадцатеричная: q=16 {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}.

Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
			A
			B
			C
			D
			E
			F

Алгебра логики – определенная часть математической логики, часто называемая исчислением высказываний. Основное понятие алгебры логики – это высказывание.

Под высказыванием понимается предложение, о котором можно сказать, истинно оно или ложно. Высказывания обозначаются латинскими буквами и могут принимать одно из двух значений: ЛОЖЬ (0) или ИСТИНА (1).

Все высказывания подразделяются на простые и сложные. Процесс получения сложного высказывания из простых носит название логическая операция.

Приняты следующие базовые логические операции: конъюнкция, дизъюнкция, инверсия.

Инверсия (логическое отрицание) представляет высказывание противоположное исходному простому высказыванию. Логическое выражение имеет смысл НЕ. Например, операцией отрицания А называют высказывание 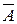(не А), которое истинно тогда, когда А ложно, и ложно тогда, когда А истинно.

Конъюнкция (логическое умножение) представляет собой сложное высказывание, истинное при одновременной справедливости всех простых высказываний из которых оно образовано. Логическое выражение имеет смысл И. Например, конъюнкцией двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда истинны оба высказывания, записывается С=А^В (С равно А и В).

Дизъюнкция (логическое сложение) представляет сложное высказывание, истинное при справедливости хотя бы одного из простых исходных высказываний. Логическое выражение имеет смысл ИЛИ. Например, дизъюнкцией двух высказываний А и В является новое высказывание С, которое истинно, если истинно хотя бы одно высказывание. Записывается С=А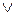В (С равно А или В).

С помощью логических операций из простых высказываний можно построить логические выражения. Первыми выполняются операции в скобках, затем: отрицание, конъюнкция, дизъюнкция.

Дата добавления: 2014-10-31