Итоговые функции

Итоговые функции

Использование абсолютной и смешанной адресации

Лабораторная № 4

1. Относительный адрес

Адреса типа A1 называют относительными. Они определяют смещение относительно текущей ячейки. Например, если в формуле ячейки B4 используется адрес A1, то это означает обращение к ячейке на один столбец левее и три строки выше. При копировании такого адреса происходит его трансформация.

2. Абсолютный адрес.

Адреса типа $A$1 называют абсолютными. Они однозначно определяют ячейку листа. При копировании такого адреса он не меняется.

3. Смешанный адрес.

Адреса типа $A1 или A$1 называют смешанными. Они состоят из фиксированной (помеченной знаком $) и относительной части. При копировании такого адреса изменяется только относительная часть.

Такие функции предназначены для обработки блока или нескольких блоков. Наиболее часто употребляются функции СУММ, СУММЕСЛИ, ПРОИЗВЕД, МИН, МАКС, СРЗНАЧ.

Пример: =СУММ(A1:B6) находит сумму элементов области, границы которой определяются координатами A1 и B6.

Задание

Выполнить оформление решения задач своего варианта на разных листах рабочей книги. Сохранить рабочую книгу в файл.

Варианты заданий

Вариант № 1.

1. Сформировать таблицу умножения.

2. Сформировать матрицу по следующему правилу. Размер матрицы вводится в отдельной ячейке.

3. Построить таблицу значений функции для и 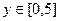с шагом 0.2.

4. Используя итоговые функции, вычислить:

,

Вариант № 2.

1. Сформировать таблицу сложения.

2. Сформировать матрицу по следующему правилу. Размер матрицы вводится в отдельной ячейке.

3. Построить таблицу значений функции для и с шагом 0.2.

4. Используя итоговые функции, вычислить:

,

Вариант № 3.

1. Сформировать таблицу умножения.

2. Сформировать квадратную матрицу порядка n по заданному образцу:

3. Построить таблицу значений функции для и 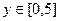с шагом 0.2.

4. Используя итоговые функции, вычислить:

,

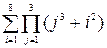
Вариант № 4.

1. Сформировать таблицу умножения.

2. Дан линейный массив 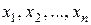. Получить действительную квадратную матрицу порядка n:

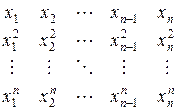
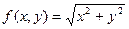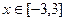3. Построить таблицу значений функции для и 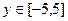с шагом 0.5.

4. Используя итоговые функции, вычислить:

,

Вариант № 5.

1. Сформировать таблицу возведения в степень.

2. Сформировать квадратную матрицу порядка n по заданному образцу:

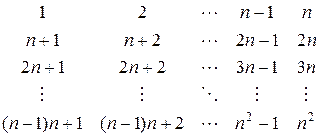
3. Построить таблицу значений функции для и 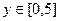с шагом 0.2.

4. Используя итоговые функции, вычислить:

,

Вариант № 6.

1. Сформировать таблицу умножения.

2. Сформировать квадратную матрицу порядка n по заданному образцу:

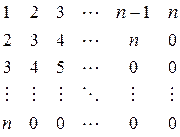
3. Построить таблицу значений функции для и 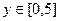с шагом 0.2.

4. Используя итоговые функции, вычислить:

,

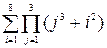
Вариант № 7.

1. Сформировать таблицу сложения.

2. Сформировать квадратную матрицу порядка n по заданному образцу:

3. Построить таблицу значений функции для и 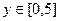с шагом 0.2.

4. Используя итоговые функции, вычислить:

,

Вариант № 8.

1. Сформировать таблицу умножения.

2. Сформировать квадратную матрицу по заданному образцу:

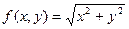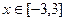3. Построить таблицу значений функции для и 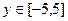с шагом 0.5.

4. Используя итоговые функции, вычислить:

,

Вариант № 9.

1. Сформировать таблицу вычитания.

2. Сформировать квадратную матрицу порядка n по заданному образцу:

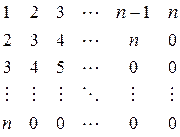
3. Построить таблицу значений функции для и 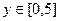с шагом 0.2.

4. Используя итоговые функции, вычислить:

,

Вариант № 10.

1. Сформировать таблицу умножения.

2. Сформировать квадратную матрицу по заданному образцу:

3. Построить таблицу значений функции для и 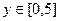с шагом 0.2.

4. Используя итоговые функции, вычислить:

,

Вариант № 11.

1. Сформировать таблицу сложения.

2. Дан линейный массив . Получить действительную квадратную матрицу порядка n:

3. Построить таблицу значений функции 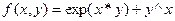для и 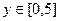с шагом 0.2.

4. Используя итоговые функции, вычислить:

,

Вариант № 12.

1. Сформировать таблицу вычитания.

2. Сформировать квадратную матрицу по заданному образцу:

3. Построить таблицу значений функции для и 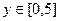с шагом 0.2.

4. Используя итоговые функции, вычислить:

,

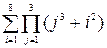
Вариант № 13.

1. Сформировать таблицу умножения.

2. Дан линейный массив . Получить действительную квадратную матрицу порядка n:

3. Построить таблицу значений функции 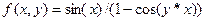для и с шагом 0.2.

4. Используя итоговые функции, вычислить:

,

Вариант № 14.

1. Сформировать таблицу сложения.

2. Сформировать квадратную матрицу по заданному образцу:

3. Построить таблицу значений функции для и с шагом 0.2.

4. Используя итоговые функции, вычислить:

,

Вариант № 15.

1. Сформировать таблицу возведения в степень.

2. Сформировать квадратную матрицу по заданному образцу:

3. Построить таблицу значений функции для и с шагом 0.2.

4. Используя итоговые функции, вычислить:

,

Дата добавления: 2014-10-31