Занятие 10. 4 стандартизация теста

Определение надежности методом расщепления

Обработка данных

1.Составляется таблица (табл. 10.3.1), где Х _{1 i} - количество правильно решенных задач i -м испытуемым - показатель успешности работы i -го испытуемого в 1-м тестировании; Х _{2 i} -показатель успешности работы i -го испытуемого во 2-м; N - объем выборки испытуемых.

Таблица 10.3.1

Определение надежности методом «тест-ретест»

i	X 1	X 2
…
N

Вычисляется коэффициент корреляции r (Х ₁, X ₂).

2. Задания теста (после повторного тестирования) разбиваются на четные и нечетные. Составляется таблица (табл. 10.3.2), где У _1i, У _2i - количество испытуемых, правильно решивших соответствующую задачу; п - количество задач.

Таблица 10.3.2

i	Y1	Y2
…
п/ 2

Для каждого столбца вычисляются средние, дисперсии и корреляция между столбцами.

- Проверяется условие применения формулы (1). Вычисляется f.

- Вычисляется f по формуле (2).

- Вычисляется f по формуле (3).

3. Составляется таблица (табл. 10.3.3), где р=Х_i/N; q=l-p; N –количество испытуемых.

Таблица 10.3.3

Таблица результатов

i	Х	р	q
…
N

- Вычисляется f ₁.

Анализ результатов. Сравнивая значения f, полученные различными способами, студенты проверяют, насколько способ вычисления влияет на результат, насколько существенно требование равенства дисперсий, насколько оценка коэффициента надежности чувствительна к количеству заданий теста.

Выводы. Делается вывод о ретестовой надежности теста, надежности расщепления, плотности; насколько эти показатели отличаются друг от друга.

Цель работы. Построение шкал теста на основе полученных «сырых» оценок.

Определение основных понятий. Стандартизация - приведение оценок теста к виду, сопоставимому с результатами других методик, измеряющих данный признак. Чаще всего это достигается или построением шкал процентилей, или шкал, основанных на z-оценках.

Шкала процентилей - разбиение выборки испытуемых на заданное число частей. Опираясь на кумулятивную кривую, процентильное шкальное значение показывает, какая часть выборки испытуемых обладает значением признака, не превосходящим заданное, т. е. с какой вероятностью можно ожидать такие значения признака.

Алгоритм построения шкалы. Проверяется гипотеза о нормальном распределении.

Если гипотеза не отклонена, то следовательно область изменения вероятности [0,1] разбивается на заданное число частей (4 части - шкала квартилей, 10 частей - шкала децилей, 100 частей - шкала собственно процентилей).

По таблице нормального распределения для границ разбиения находится соответствующий квантиль. Этот квантиль является искомым шкальным значением.

Z -оценки - выражение шкальных значений в единицах стандартного отклонения (среднеквадратичного отклонения).

При выполнении условия нормального распределения оценок, шкалы, основанные на z -оценках, являются шкалами интервалами. Линейное преобразование, допустимое для шкал интервалов, позволяет привести их к удобному виду:

S = А + В ´ Z,

здесь А - позволяет сдвинуть начало отсчета и освободиться от отрицательных шкальных значений, множитель В изменяет масштаб, что позволяет перейти от дробных к целым шкальным значениям.

Z -оценка может быть получена линейным преобразованием:

где х - непреобразованная тестовая оценка; М - оценка математического ожидания (среднее арифметическое); s - оценка среднеквадратичного отклонения; т. е. z -оценка путем центрирования (сдвига точки отсчета в 0) и нормирования (переход к единицам среднеквадратичного отклонения).

Если известна вероятность того, что величина признака не превосходит некоторое значение, то 2-оценка будет равна квантилю этой вероятности и может быть найдена из таблицы нормального распределения.

Математический аппарат. Критерии проверки гипотезы о нормальном распределении.

При выборках объемом больше 50 рекомендуется применять критерий c².

Порядок работы. Даны результаты обследования группы испытуемых (N = 63) с помощью теста Айзенка (см. прил. 10.4.1). Для каждого из показателей (экстраверсии и нейротизма) следует:

1. Построить гистограмму распределения частот. Проверить гипотезу о нормальном распределении с помощью критерия c².

2. Построить кривую накопленных частот (кумуляту).

3. Построить процентильную шкалу децилей.

4. Построить z -шкалу.

5. С помощью коэффициента корреляции Пирсона проверить гипотезу о статистической независимости показателей нейротизма и интроверсии.

Анализ результатов. Из свойств нормального распределения следует, что для показателей теста Айзенка

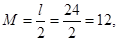
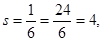
где М - математическое ожидание, l - размах, s - среднеквадратичное отклонение.

Сравните полученные вами оценки с теоретическими.

Приложение 10.4.1

Показатель экстраверсии:

4;12;10; 9;14;10; 8; 7; 12; 7;13;17;13; 12;14; 15;18;17; 5; 7;15;12;16; 8;15; 10; 11; 8; 14; 13; 12; 8; 13; 14; 8; 4; 13; 4; 10; 12; 6; 12; 14; 10; 11; 9; 9; 16; 17; 19;10;20;16;11;11;20; 9;11;13; 8;11;11; 6.

Показатель нейротизма:

10; 11; 19; 14; 9:20; 7; 20; 20; 19; 9; 7; 10; 14; 18; 13; 11; 15; 9; 11; 13; 19: 17; 19; 16; 8;21;17;16; 5; 16; 15; 13; 21; 14; 10; 4; 19; 12; 20; 21; 16: 21; 7;12;11; 4;13; 13; 6;12;16;23;19;15;17;11; 4;13;22;20;15;15.

Занятие 10.5 ИССЛЕДОВАНИЕ ЭКСТРАВЕРСИИ-ИНТРОВЕРСИИ И НЕЙРОТИЗМА (ОПРОСНИК АЙЗЕНКА)

Вводные замечания. Автор двухфакторной модели личности Г. Айзенк в качестве показателей основных свойств личности использовал экстраверсию-интроверсию и нейротизм^*. В общем смысле экстраверсия - это направленность личности на окружающих людей и события, интроверсия - направленность личности на ее внутренний мир, а нейротизм - понятие, синонимичное тревожности, - проявляется как эмоциональная неустойчивость, напряженность, эмоциональная возбудимость, депрессивность.

* Позднее Айзенк ввел еще одно измерение личности - психотизм, под которым понимал склонность субъекта к агрессии, жестокости, аутизму, экстравагантности, демонстративности.

Эти свойства, составляющие структуру личности по Айзенку, генетически детерминированы. Их выраженность связана со скоростью выработки условных рефлексов и их прочностью, балансом процессов возбуждения - торможения в центральной нервной системе и уровнем активации коры головного мозга со стороны ретикулярной формации. Однако наиболее разработанным из двух названных свойств на физиологическом уровне в теории Айзенка является учение об экстраверсии-интроверсии. В частности, различия между экстравертами и интровертами Айзенку и его последователям удалось установить более чем по пятидесяти физиологическим показателям.

Так, экстраверт, по сравнению с интровертом, труднее вырабатывает условные рефлексы, обладает большей терпимостью к боли, но меньшей терпимостью к сенсорной депривации, вследствие чего не переносит монотонности, чаще отвлекается во время работы и т. п. Типичными поведенческими проявлениями экстраверта являются общительность, импульсивность, недостаточный самоконтроль, хорошая приспособляемость к среде, открытость в чувствах. Он отзывчив, жизнерадостен, уверен в себе, стремится к лидерству, имеет много друзей, несдержан, стремится к развлечениям, любит рисковать, остроумен, не всегда обязателен.

У интроверта преобладают следующие особенности поведения: он часто погружен в себя, испытывает трудности, устанавливая контакты с людьми и адаптируясь к реальности. В большинстве случаев интроверт спокоен, уравновешен, миролюбив, его действия продуманны и рациональны. Круг друзей у него невелик. Интроверт высоко ценит этические нормы, любит планировать будущее, задумывается над тем, что и как будет делать, не поддается моментальным побуждениям, пессимистичен. Интроверт не любит волнений, придерживается заведенного жизненного порядка. Он строго контролирует свои чувства и редко ведет себя агрессивно, обязателен.

На одном полюсе нейротизма (высокие оценки) находятся так называемые нейротики, которые отличаются нестабильностью, неуравновешенностью нервно-психических процессов, эмоциональной неустойчивостью, а также лабильностью вегетативной нервной системы. Поэтому они легко возбудимы, для них характерны изменчивость настроения, чувствительность, а также тревожность, мнительность, медлительность, нерешительность.

Другой полюс нейротизма (низкие оценки) - это эмоционально-стабильные лица, характеризующиеся спокойствием, уравновешенностью, уверенностью, решительностью.

Показатели экстраверсии-интроверсии и нестабильности-стабильности взаимонезависимы и биполярны. Каждый из них представляет собой континуум между двумя полюсами крайне выраженного личностного свойства. Сочетание этих двух в разной степени выраженных свойств и создает неповторимое своеобразие личности. Характеристики большинства испытуемых располагаются между полюсами, чаще где-то близко к центру. Удаленность показателя от центра свидетельствует о степени отклонения от среднего с соответствующей выраженностью личностных свойств.

Связь факторно-аналитического описания личности с четырьмя классическими типами темперамента - холерическим, сангвиническим, флегматическим, меланхолическим отражается в «круге Айзенка» (рис. 10.5.1): по горизонтали в направлении слева направо увеличивается абсолютная величина показателя экстраверсии, а по вертикали снизу вверх уменьшается выраженность показателя стабильности.

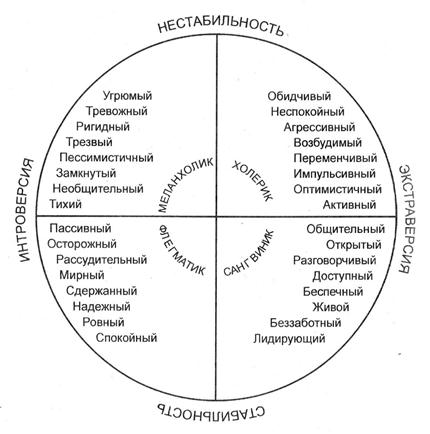
Рис. 10.5.1. «Круг Айзенка».

Опросник Г. Айзенка имеет две параллельные, эквивалентные формы - А и В которые могут применяться как одновременно - для большей достоверности результатов, так и раздельно, с интервалом во времени - для проверки надежности опросника или с целью получения результатов исследований в динамике.

Цель занятия. Исследование экстраверсии-интроверсии и нейротизма.

Оснащение. Бланк опросника Айзенка (форма А) (см. прил. 10.5.1), ответный лист (форма 38).

ПРОТОКОЛ ЗАНЯТИЯ Форма 38

Фамилия, имя, отчество......................................................…………………………………. Дата.......………………

Возраст...................…………………………………. Образование.....................................................…………………

Дата добавления: 2014-10-31