
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнения Шредингера
|
|
|
|
Установите соответствие уравнений Шредингера их физическому смыслу:
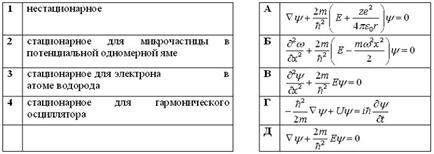
1) 1-А, 2-Б, 3-Г, 4-В
2) 1-В, 2-Б, 3-А, 4-Д
3) 1-Г, 2-Б, 3-А, 4-В
4) 1-Г, 2-В, 3-А, 4-Б
Решение:
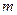 - масса частицы, - масса частицы, 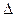 - оператор Лапласа, - оператор Лапласа, 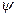 - волновая функция характеризующая состояние частицы, - волновая функция характеризующая состояние частицы, 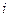 - мнимая единица, - мнимая единица, 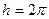 ħ – постоянная Планка. ħ – постоянная Планка.
| ||
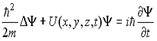
| Это уравнение Шредингера для нестационарных состояний, зависящее от времени. Это означает, что силовое поле, в котором движется микрочастица, является нестационарным, т.е. потенциальная функция 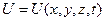 частицы в силовом поле зависит от времени частицы в силовом поле зависит от времени 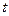 . .
| |
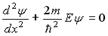
| Уравнение называется уравнением Шредингера для стационарных состояний, когда микрочастица находится в потенциальной одномерной яме. Стационарное состояние – это состояние с фиксированными значениями энергии. Силовое поле, в котором движется микрочастица, является стационарным, т.е. потенциальная функция 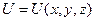 частицы в силовом поле не зависит от времени частицы в силовом поле не зависит от времени 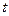 . .
| |
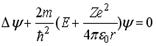
| Это стационарное уравнение Шредингера, которое описывает состояние электрона в атоме водорода. | |
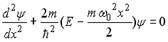
| Уравнение Шредингера, описывающее стационарные состояния гармонического осциллятора. Гармонический осциллятор – это система, совершающая одномерное движение под действием квазиупругой силы. Примерами гармонического осциллятора являются физический, математический и пружинный маятники. | |
| Ответ: вариант 4. |
Нестационарным уравнением Шредингера является уравнение…
1) 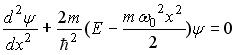
2) 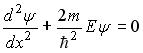
3) 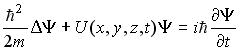
4) 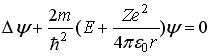
Решение:
Уравнение Шредингера для нестационарных состояний имеет вид
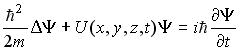 Это означает, что силовое поле, в котором движется микрочастица, является нестационарным, т.е. потенциальная функция
Это означает, что силовое поле, в котором движется микрочастица, является нестационарным, т.е. потенциальная функция 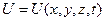 частицы в силовом поле зависит от времени частицы в силовом поле зависит от времени 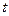 .
Ответ: вариант 3. .
Ответ: вариант 3.
|
Стационарное уравнение Шредингера в общем случае имеет вид: 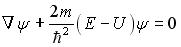 , где U – потенциальная энергия микрочастицы. Электрону в атоме водорода соответствует уравнение …
, где U – потенциальная энергия микрочастицы. Электрону в атоме водорода соответствует уравнение …
1) 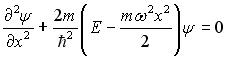
2) 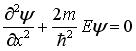
3) 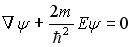
4) 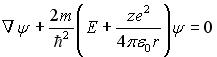
Решение:
Стационарное уравнение Шредингера, описывающее состояние электрона в атоме водорода имеет вид
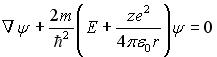 Ответ: вариант 4.
Ответ: вариант 4.
|
Стационарное уравнение Шредингера в общем случае имеет вид: 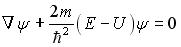 , где U – потенциальная энергия микрочастицы. Электрону, движущемуся в одномерной потенциальной яме с бесконечно высокими стенками, соответствует уравнение …
, где U – потенциальная энергия микрочастицы. Электрону, движущемуся в одномерной потенциальной яме с бесконечно высокими стенками, соответствует уравнение …
1) 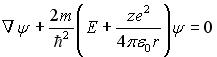
2) 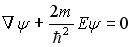
3) 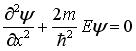
4) 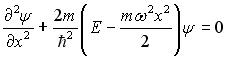
Решение:
Уравнение Шредингера для стационарных состояний, когда микрочастица находится в потенциальной одномерной яме, имеет вид
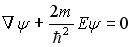 Ответ: вариант 4.
Ответ: вариант 4.
|
Стационарное уравнение Шредингера в общем случае имеет вид: 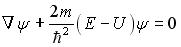 , где U – потенциальная энергия микрочастицы. Линейному гармоническому осциллятору соответствует уравнение …
, где U – потенциальная энергия микрочастицы. Линейному гармоническому осциллятору соответствует уравнение …
1) 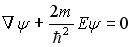
2) 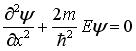
3) 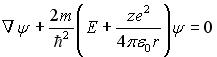
4) 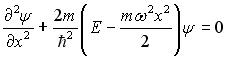
Решение:
Уравнение Шредингера, описывающее стационарные состояния гармонического осциллятора имеет вид
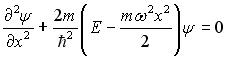 Ответ: вариант 4.
Ответ: вариант 4.
|
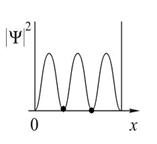
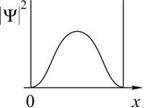
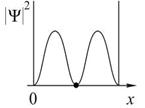
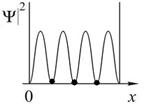
На рисунках приведены картины распределения плотности вероятности нахождения микрочастицы в потенциальной яме с бесконечно высокими стенками. Состоянию с квантовым числом n =2 соответствует
1) 2)
2) 
3) 4)
4) 
Решение:
Во всех четырех графиках описана плотность вероятности обнаружения частицы на различных расстояниях от стенок ямы, равная 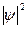 . На графиках указаны узлы (черные точки), в которых частица не может находиться. Каждому состоянию частицы с определенным квантовым числом соответствует свой график. Для состояния частицы с квантовым числом . На графиках указаны узлы (черные точки), в которых частица не может находиться. Каждому состоянию частицы с определенным квантовым числом соответствует свой график. Для состояния частицы с квантовым числом 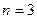 соответствует первый график (вариант 1), для соответствует первый график (вариант 1), для 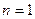 соответствует второй график (вариант2), соответствует второй график (вариант2), 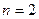 - соответствует третий график (вариант 3), для четвертого - - соответствует третий график (вариант 3), для четвертого - 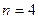 .
Ответ: вариант 3. .
Ответ: вариант 3.
|
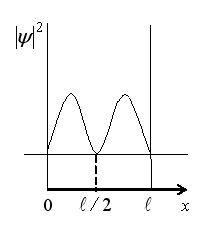
На рисунке изображена плотность вероятности обнаружения микрочастицы на различных расстояниях от «стенок» ямы. Вероятность ее обнаружения на участке 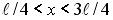 равна …
равна …
1) 3/4 2) 1/4 3) 0 4) 1/2
Решение:
Из графика видно, что участок от 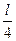 до до 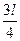 состоит из двух промежутков, где может находится частица: [ состоит из двух промежутков, где может находится частица: [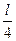 ; ;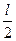 ] и [ ] и [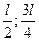 ]. В точке с координатой ]. В точке с координатой 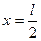 (на рис. отмечено черной точкой) частица не может находиться, т.е. не может находиться в середине «ямы», в то время как одинаково часто может пребывать в ее правой и левой частях. Следовательно, вероятность обнаружения частицы на участке (на рис. отмечено черной точкой) частица не может находиться, т.е. не может находиться в середине «ямы», в то время как одинаково часто может пребывать в ее правой и левой частях. Следовательно, вероятность обнаружения частицы на участке 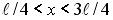 равна равна 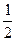 .
Ответ: вариант 4. .
Ответ: вариант 4.
| 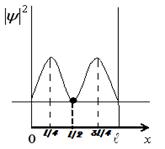 Рис.
Рис.
|
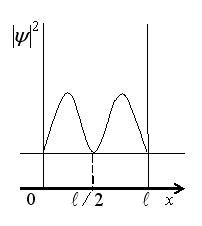
На рисунке изображена плотность вероятности обнаружения микрочастицы на различных расстояниях от «стенок» ямы. Вероятность ее обнаружения в центре ямы равна …
1) 0 2) 1/2 3) 1/4 4) 3/4
| Решение: Вероятность обнаружения микрочастицы в центре ямы равна нулю, так как она не может находиться в середине «ямы». Ответ: вариант 1. | 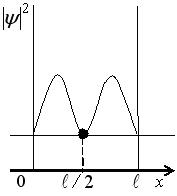
|
РАЗДЕЛ VI. ФИЗИКА АТОМА, АТОМНОГО ЯДРА
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 20350; Нарушение авторских прав?; Мы поможем в написании вашей работы!