Элементы теории множеств

Предмет дискретной математики (ДМ).

Библиографический список

1. Никитин Н.Н. Курс теоретической механики: учебник для машиностроит. и приборостроит. спец. вузов / Н.Н. Никитин. – М.: Высш. шк., 1990. 607 с.

2. Бутенин Н.В. Курс теоретической механики: в 2х т. / Н.В. Бутенин, Я.Л. Лунц, Д.Р. Меркин. – СПб.: Лань, 2002. 736 с.

3. Тарг С.М. Краткий курс теоретической механики / С.М. Тарг. – М: Высш. шк., 2008. 416 с.

4. Цывильский В.Л. Теоретическая механика / В.Л. Цывильский. – М: Высш. шк., 2008. 368 с.

5. Переславцева Н.С. Теоретическая механика: учеб. пособие / Н.С. Переславцева, Н.П. Бестужева. – Воронеж: ВГТУ, 2009. – 157 с.

6. Мещерский И.В. Задачи по теоретической механике / И.В. Мещерский. – СПб.: Лань, 2001. 448 с.

7. Сборник заданий для курсовых работ по теоретической механике: учеб. пособие для техн. вузов / под ред. А.А. Яблонского. – М.: Интеграл-Пресс, 2006. 384 с.

содержание

Программа курса....................... 1

Статика........................... 2

Кинематика......................... 3

Кинематика твердого тела................. 4

Содержание контрольных заданий, выбор вариантов,

порядок выполнения работ, общие

пояснения к тексту задач................. 5

Принятые обозначения.................... 7

Задачи к контрольным заданиям.............. 10

Статика. Задача С1.................... 10

Кинематика. Задача К1.................. 16

Задача К2.................. 22

Контрольные вопросы.................... 29

Библиографический список................. 31

Программа, методические указания

и контрольное задание № 1

(статика, кинематика)

по дисциплине

«Теоретическая механика»

для бакалавров всех направлений

заочной и заочной ускоренной форм обучения

Составители:

Переславцева Наталья Сергеевна

Бестужева Наталья Петровна

В авторской редакции

Компьютерный набор Н.С. Переславцевой

Подписано к изданию 30.10.2012.

Уч.-изд. л. 1,9.

ФГБОУ ВПО

«Воронежский государственный технический университет»

394026 Воронеж, Московский просп., 14

Значение ДМ в решении современных задач в области информационных технологий.

ДМ – область математики, изучающая свойства дискретных конечных структур (конечные графы, некоторые математические модели преобразователей информации, конечные группы).

Классическая математика (КМ). Для КМ – предел и непрерывность. Последовательность развития ДМ: теория чисел – комбинаторный анализ – дискретная теория вероятностей – математическая логика – математическая кибернетика. Роль ВТ.

2. Разделы ДМ:

1. Теория множеств.

2. Теория отношений.

3. Теория графов.

4. Теория помехоустойчивого кодирования.

5. Комбинаторный анализ.

6. Теория абстрактных цифровых автоматов.

7. Математическая логика.

8. Теория алгоритмов.

9. Теория переключательных схем.

10. Теория чисел.

Изучаем общие свойства множеств. Основоположник теории множеств - Кантор. Приняты аксиоматические системы.

Понятие множество не определяется, а находится на интуитивном уровне.

В ДМ множество - конечная совокупность каких-либо объектов. Множество определяется принадлежащими ему элементами.

Обозначается: А, В, С, …, Х, У,…

Элементы множества: а, b, с, …, х, у, 1, 2, 3

Пишут: М = {а, b, с}; Х = {1, 2, 3, 4, {5}},…

Принадлежность элемента множеству:

a Î M; {5} Î X;

d Ï M; 6 Ï X.

Порядок расположения элементов внутри множества не учитывается:

М = {a, b, c}; M = {c, a, b},…

Одинаковые элементы не рассматриваются:

M = {a, b, c} = {a, a, a, b, c, c}

A = {{a},{a,b,c,{d}},d} – в множестве 3 элемента!

Равенство множеств: M = N

Множества M и N называются равными, если каждый элемент множества M есть в N, а каждый элемент N есть в M.

M = {a, b, c} = N = {a, b, c}

Элементарное множество – это множество, содержащее один элемент: С={7}.

Пустое множество – множество, не содержащее элементов. Обозначается Æ.

Подмножество. Множество А, все элементы которого принадлежат множеству В, называется подмножеством множества B. Говорят: В включает А. Пишут:

A 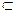B

A = {1, 2, 3, {4}}; B = {1, 2, 3, {4}, 5, 6}

Если А может быть равно В, то пишут

A B

М ножество подмножеств – это множество, элементами которого являются все подмножества множества А (или В,…).

Пусть А = {а, в, с}; Р(А) – множество подмножеств. Тогда

Р(А) = {а, в, с, {а, в}, {а, с}, {в, с}, {а, в, с}}.

Мощность множества в DM – число его элементов. Обозначается: |A| = 3;

n = 3; |P(A)| = 2ⁿ.

Задание множеств:

1. Перечислением элементов.

2. С помощью определяющего свойства (описание элементов). A = {x|R(x)}

Например: А = {х | х= 4 } 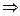А = {2, -2}.

Универсальное множество (универсум) U - это множество всех объектов, с которыми оперируют при решении данной задачи.

Круги Эйлера (диаграммы Эйлера – Венна) – наглядный способ выполнения операций над множествами.

U - обозначается прямоугольником; множества – круги внутри прямоугольника.

Операции над множествами:

1. Объединение: C = AB

A = {0, 1, 2}; B = {1, 2, 3, 4}

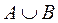= {0, 1, 2, 3, 4}

2. Пересечение C = A ∩ B = {1, 2}

3. Разность 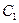= A \ B = {0}

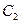= B \ A = {3, 4}

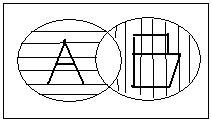
4. Дополнение = U \ A

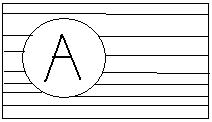
5. Симметрическая разность С = A ÷ B

C = (A \ B) (B \ A)

C = {0, 3, 4}

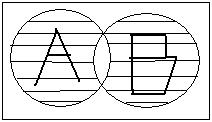
Приоритеты операций: , ∩, \, ÷,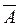

Основные теоремы алгебры множеств:

1a) AB = BA 1б) AB = BA

2a) A(BC) = (AB)C 2б) A(BC) = (AB)C

3a) ABC = (AB)(AC) 3б) A(BC) = ABAC

4a) AÆ = A 4б) АÆ = Æ

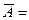5a) A= U 5б) AÆ

6a) AU = U 6б) AU = A

7a) 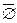= U 7б) 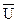= Æ

8a) AA = A 8б) AA = A

9a) AAB = A 9б) A(AB) = A – закон поглощения

10a) = 10б) 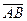= – теоремы де Моргана

11) если AB = U, а AB = Æ,

то A = ; B =

12) = U\A

13) = A

14) A\B = A

15) A÷B = AB

16) A÷B = B÷A

17) (A÷B) ÷C = A÷ (B÷C)

18) Æ÷A = A÷Æ = A

19) A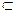B, если AB = A, или AB = B, или A\B = Æ, 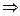A= Æ

20) A = B, если A÷B = Æ

21) ABA= A - закон склеивания

22) AB = AB

23) = AB

24) AB÷AC = A(B÷C)

25) Если в алгебр. выражении многократно используется операция или,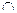

26) то порядок выполнения операций произвольный

При работе в алгебре множеств:

1. Убирается самое длинное дополнение с использованием теорем № 10 (а, б);

2. Все операции заменяются на , , ;

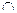3. Операцию следует рассматривать как сложение, а - как умножение.

Пример 1. Упростить:

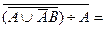
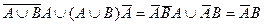
(№22) Æ(№5)

Пример 2. Доказать: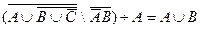

1)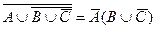 (№10)

2) (№9)

3)

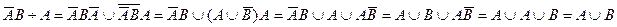
(№22, №8)

Пример 3. Упростить: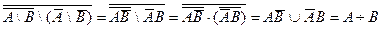

Дата добавления: 2014-10-31