U-критерий Манна-Уитни

Пример

Ограничения критерия Q

1. В каждой из сопоставляемых выборок должно быть не менее 11 на­блюдений. При этом объемы выборок должны примерно совпадать. Е.В. Гублером указываются следующие правила:

а) если в обеих выборках меньше 50 наблюдений, то абсолютная ве­личина разности между n₁ и n₂ не должна быть больше 10 на­блюдений;

б) если в каждой из выборок больше 51 наблюдения, но меньше 100, то абсолютная величина разности между n₁ и n₂ не должна быть больше 20 наблюдений;

в) если в каждой из выборок больше 100 наблюдений, то допуска­ется, чтобы одна из выборок была больше другой не более чем в 1,5-2 раза (Гублер Е.В., 1978, с. 75).

2. Диапазоны разброса значений в двух выборках должны не совпадать между собой, в противном случае применение критерия бессмыслен­но. Между тем, возможны случаи, когда диапазоны разброса значе­ний совпадают, но, вследствие разносторонней асимметрии двух рас­пределений, различия в средних величинах признаков существенны (Рис. 2.3., 2.4).

У предполагаемых участников психологического эксперимента, моделирующего деятельность воздушного диспетчера, был измерен уро­вень вербального и невербального интеллекта с помощью методики Д. Векслера. Было обследовано 26 юношей в возрасте от 18 до 24 лет (средний возраст 20,5 лет). 14 из них были студентами физического факультета, а 12 - студентами психологического факультета Ленинград­ского университета (Сидоренко Е.В., 1978). Показатели вербального интеллекта представлены в Табл. 2.1.

Можно ли утверждать, что одна из групп превосходит другую по уровню вербального интеллекта?

Таблица 2.1

Индивидуальные значения вербального интеллекта в выборках студен­тов физического (n₁ =14)и психологического (n₂ ⁼12) факультетов

	Студенты-физики		Студенты - психологи
	Код имени испытуемого	Показатель вербального интеллекта		Код имени испытуемого	Показатель вербального интеллекта
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14.	И.А К.А. К.Е. П.А. С.А. Ст.А. Т.А. Ф.А. Ч.И. Ц.А. См.А. К.Ан. Б.Л. Ф.В.		1. 2. 3. 4. 5. 6. 7. 8. 9.	н.т. о.в. Е.В. Ф.О. и.н. и.ч. и.в. К.О. p.p. Р.И. O.K. н.к.

Упорядочим значения в обеих выборках, а затем сформулируем гипотезы:

H₀: Студенты-физики не превосходят студентов-психологов по уровню вербального интеллекта.

H₁: Студенты-физики превосходят студентов-психологов по уровню вербального интеллекта.

Таблица 2.2

Упорядоченные по убыванию вербального интеллекта ряды индивидуальных значений в двух студенческих выборках

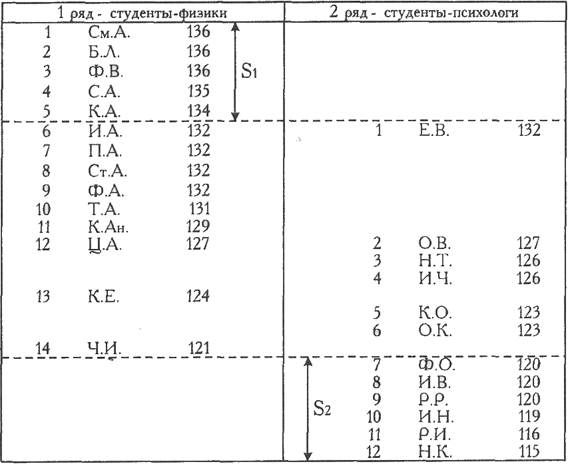
Как видно из Табл. 2.2, мы правильно обозначили ряды: пер­вый, тот, что "выше" - ряд физиков, а второй, тот, что "ниже" - ряд психологов.

По Табл. 2.2 определяем количество значений первого ряда, ко­торые больше максимального значения второго ряда: S₁=5.

Теперь определяем количество значений второго ряда, которые меньше минимального значения первого ряда: S₂=6.

Вычисляем Q_ЭМП по формуле:

Q_ЭМN=S₁+S₂=5+6 = 11

По Табл.II Приложения 1 определяем критические значения Q для n₁=14, n₂=12:

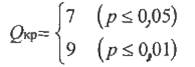
Ясно, что чем больше расхождения между выборками, тем боль­ше величина Q. Н_о отклоняется при Q_эмп>Q_кp, а при Q_эмп <Q_кp мы будем вынуждены принять Н_о.

Построим "ось значимости".

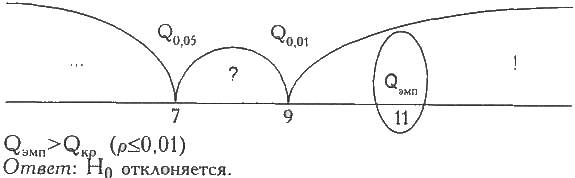
Принимается H₁. Студенты-физики превосходят студентов-психологов по уровню вербального интеллекта (р< 0,01). Отметим, что в тех случаях, когда эмпирическая величина критерия оказывается на границе зоны незначимости, мы имеем право утверждать лишь, что различия достоверны при р≤ 0,05, если же оно оказывается между двумя критическими значениями, то мы можем утверждать, что р< 0,05.

Если эмпирическое значение критерия оказывается на границе зоны значимости, р≤ 0,01, в зоне значимости - что р< 0,01

Поскольку уровень значимости выявленных различий достаточно высок (р< 0,01), мы могли бы на этом остановиться. Однако если ис­следователь сам психолог, а не физик, вряд ли он на этом остановится. Он может попробовать сопоставить выборки по уровню невербального интеллекта, поскольку именно невербальный интеллект определяет уро­вень интеллекта в целом и степень его организованности (см., напри­мер: Бергер М.А., Логинова НА., 1974).

Мы вернемся к этому примеру при рассмотрении критерия Манна-Уитни и попытаемся ответить на вопрос о соотношении уровней не­вербального интеллекта в двух выборках. Быть может, психологи еще окажутся в более высоком ряду!

АЛГОРИТМ 3 Подсчет критерия Q Розенбаума 1. Проверить, выполняются ли ограничения: n₁•n₂ ≥11, n₁ n₂≈n₂ Упорядочить значения отдельно в каждой выборке по степени возрастания признака. Считать выборкой 1 ту выборку, значения в ко­торой предположительно выше, а выборкой 2 - ту, где значения предположительно ниже. 3. Определить самое высокое (максимальное) значение в выборке 2. 4. Подсчитать количество значений в выборке 1, которые выше макси­мального значения в выборке 2. Обозначить полученную величину как S₁. 5. Определить самое низкое (минимальное) значение в выборке 1. 6. Подсчитать количество значений в выборке 2, которые ниже мини­мального значения выборки 1. Обозначить полученную величину как S₂. 7. Подсчитать эмпирическое значение Q по формуле: Q=S₁+S2- 8. По Табл. I Приложения I определить критические значения Q для данных n₁ и n₂. Если Q_эмп равно Q_0,05 или превышает его, Н₀ отвергается. 9. При n₁•n₂ >26сопоставить полученное эмпирическое значение с Q_{кp =} 8 (р≤ 0,05) иQ_{кp =} 10(p≤ 0,01). Если Q_эмп превышает или по крайней мере равняется Q_{кp =} 8, H₀отвергается.

Дата добавления: 2014-10-31