Введение. Глава12. Коммуникации в организациях

КАЗАНЬ

ДАВЫДОВ А.П.

.

ВИДЫ ПРОФЕССИОНАЛЬНО ОРИЕНТИРОВАННОЙ КОММУНИКАЦИИ

Часть IV

Глава 12. Коммуникации в организациях........................... 481

12.1. Коммуникация как функция управления организацией..... 481

12.2. Особенности внутренних коммуникаций в организации.... 488

12.3. Виды коммуникаций в организациях...................... 494

12.4. Формы деловой коммуникации в организации............. 500

12.5. Особенности маркетинговых коммуникаций............... 508

Выводы............................................................. 511

Контрольные вопросы................................................ 511

Литература........................................................ 512

Глава 13. Политическая коммуникация............................. 513

13.1. Понятие политической коммуникации.................... 513

13.2. Структура, средства и модели политической

коммуникации........................................... 517

13.3. Электоральная политическая коммуникация............... 522

13.4. Политическая коммуникация в информационном

обществе................................................ 530

Выводы............................................................. 543

Контрольные вопросы................................................ 544

Литература........................................................ 544

Глава 14. Публичная коммуникация................................ 545

14.1. Публичная коммуникации и ее формы.................... 545

14.2. Жанры публичной коммуникации......................... 547

14.3. Устная публичная учебная коммуникация.................. 551

14.4. Устная деловая публичная коммуникация.................. 556

14.5. Устная публицистическая коммуникация.................. 569

Выводы............................................................. 575

Контрольные вопросы................................................ 576

Литература........................................................ 576

Глава 15. Межкультурная коммуникация............................ 578

15.1. Понятие межкультурной коммуникации................... 578

15.2. Уровни межкультурной коммуникации.................... 584

15.3. Формы межкультурной коммуникации..................... 589

15.4. Лингвокультурологические аспекты межкультурной

коммуникации........................................... 596

15.5. Типы восприятия межкультурных различий............... 605

Выводы............................................................. 609

Контрольные вопросы................................................ 610

Литература........................................................ 611

ОСНОВЫ ТЕПЛОПЕРЕДАЧИ И МЕХАНИКИ ЖИДКОСТИ

Теплопередача является частью теплотехники – науки о теплоте, выработке энергии, преобразование одного вида энергии в другой. Теплопередача уделяет главное внимание процессам переноса тепла в различных конструкциях, устройства и машинах.

Теплопередача, как часть учения о теплоте была заложена великим российским ученым М.В. Ломоносовым. С развитием техники вопросы переноса тепла стали приобретать первостепенную роль. Так, например, в 19 веке была опубликована работа О. Рейнольдса в которой устанавливается единство процессов переноса тепла и количества движения – «Гидродинамическая теория теплообмена».

В развитие науки о теплопередаче большой вклад внесли российские ученые М.Ф Окотов, И.А. Вышнеградский, Д.И. Менделеев, А.А. Гухман, М.А Михеев, А.В. Лыков, М.В. Кирпичев. Так М.В. Кирпичевым была разработана методология проведения моделирования, проведения экспериментальных исследований тепловых устройств. Им была разработана общая методология исследований, обработки и обобщения опытных данных. Разработана теория теплового моделирования.

Рассматриваемые в второй главе вопросы механики жидкости непосредственно связаны с проектированием и конструированием всех современных технических устройств.

Механика жидкости – наука, рассматривающая статику, динамику и прикладную механику жидкости, позволяющую непосредственно определять, проектировать и конструировать гидротехнические сооружения гидравлические машины, трубопроводы различного назначения т.п.

Первые данные в области механики жидкости относятся к 237-212 годам до нашей эры. Закон о равновесии тела погруженного в жидкость – закон древнегреческого ученого Архимеда. В средние века в познание механики жидкости был внесен большой вклад учеными Европы - Стевином, Торичелли, Паскалем.

В развитие областей механики жидкости большой вклад внесли российские ученые Элейлер Д. Бернулли Жуковский Петров.

В развитие современной механики жидкости важную роль сыграли труды ученых: В.Г Шухова, А.Н.Крылова, Н.Н. Павловского, В.Д. Альшуля, Л.Г. Лойцянского, Евриинова и д.р.

Современный уровень развития механики жидкости и теплопередачи позволяют решать большой сектор технических проблем.

Глава 1

ОСНОВЫ ТЕОРИИ ТЕПЛОЕПЕРЕДАЧИ

1.1Общие сведения

Теория теплопередачи – это наука о процессах передачи тепла от более нагретого тела к менее нагретому телу. Целый ряд важных вопросов техники, конструирования машин, проектирования и строительства зданий и сооружений осуществляется на основе теории теплообмена.

1.2 Виды передачи тепла.

Теплообмен представляет собой совокупность сложных процессов. Для облегчения изучения процесса теплообмена его разделяют на ряд простых процессов. Различают три принципиально отличных друг от друга процесса теплообмена – теплопроводность, конвекцию и тепловое излучение.

Теплопроводность происходит при непосредственном ударении частиц вещества (молекул,), сопровождающемся обменом тепловой энергии движения. Такой процесс теплообмена может происходить в любых телах. Перенос тепла в этом случае зависит от агрегатного состояния тела.

Теплопроводность жидких и газообразных тел незначительна. Твердые тела обладают большей теплопроводностью. Тела с малой теплопроводностью называют теплоизоляционными. Теплоизоляционными материалами считаются материалы, коэффициент теплопроводности которых меньше 0.2 вт/м К Процесс теплообмена конвекцией происходит только в жидкостях и газах. Конвекция представляет собой процесс переноса тепла путем перемещения и перемешивания частиц жидкости или газа.

Перемещение частиц жидкости или газа обусловленное разностью плотностей, то такое перемещение называют естественной конвекцией. При естественной конвекции нагретые объемы теплоносителя поднимаются, охладившиеся опускаются.

Если жидкость или газ перемещается с помощью технического устройства (насоса, вентилятора, эжектора и т. д), то такой процесс теплообмена называют вынужденной конвекцией. Теплообмен при вынужденной конвекцией происходит значительно интенсивнее, чем при естественной конвекции.

Процесс теплообмена тепловым излучением состоит в переносе тепла от одного тела к другому электромагнитными волнами. Лучистая энергия возникает в телах за счет других видов энергии, главным образом тепловой. Электромагнитные волны распространяются от поверхности тела во все стороны со скоростью света. Встречая на своем пути другие тела, лучистая энергия может ими частично поглощаться, превращаясь снова в теплоту.

При изучении отдельных видов теплообмена используют следующие общие аксиомы и определения.

1. Передача тепла от одного тела к другому, а также между частицами данного тела происходит только при наличии разности температур.

2.Тепловой поток всегда направлен в сторону более низкой температуры.

3. Количество теплоты, переносимой в единицу времени, называется тепловым потоком .

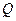Отношение 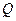к единице площади F м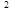называется удельным тепловым потоком:

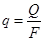(1.2.1)

4. Распределение температуры в телах обычно определяется с помощью температурного поля, т.е. совокупности значений температур во всех точках изучаемого пространства в заданный момент времени. Температура различных точек тела t может быть определена координатами x, y, z и временем 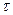, т.е.

t=f(x, y, z, 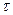) (1.2.2).

Рис. 1.2.1

5.Температурное поле, которое изменяется с течением времени, называется нестационарным (неустановившимся). При этом тепловой режим и тепловой поток будут тоже нестационарными.

6. Если температура в любой точке тела с течением времени не изменяется, то температурное поле называется стационарным (установившимся). В этом случае тепловой режим и тепловой поток будут также стационарными.

Стационарное температурное поле можно охарактеризовать зависимостью

t=f(x, y, z) (1.2.3).

Простейшим температурным полем является одномерное стационарное поле, которое характеризуется изменением температуры в направлении одной координатной оси. Такое температурное поле можно выразить уравнением

t=f(x) (1.2.4).

7. Изотермической поверхностью принимается геометрическое место точек с одинаковой температурой. Температурное поле в рассматриваемом теле или системе тел характеризуется изотермической поверхностью. Такие поверхности могут быть замкнуты. Изотермические поверхности между собой никогда не пересекаются.

8. Если изотермические поверхности пересечь плоскостью, то на плоскости сечения получим изотермические линии, называемые изотермами. Взаимное расположение изотерм (Рис.1) наглядно характеризует распределение температур в теле и интенсивность изменения температуры в различных направлениях.

9. Наибольшее изменение температуры на единицу длины получается в направлении нормали к изотермическим поверхностям. Производная температуры по нормали к изотермической поверхности называется температурным градиентом и обозначается grad, его размерность- 0С/м.

1.3. ЗАКОН ФУРЬЕ И КОЭФФИЦИЕНТ ТЕПЛОПРОВОДНОСТИ

Основным законом теплопроводности является Закон Фурье (1822 г.).Он устанавливает взаимосвязь между удельным тепловым потоком и температурным градиентом:

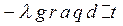(1.2.5),

где 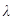- множитель пропорциональности, который называется коэффициентом теплопроводности и имеет размерность .

Знак минус указывает, что вектор теплового потока направлен в сторону, противоположную температурному градиенту.

Из уравнения (1.4) видно, что коэффициент теплопроводности количественно равен удельному тепловому потоку при температурном градиенте, равном единице - изменение температуры в 10 на единицу длины.

Коэффициент теплопроводности является важной теплофизической характеристикой вещества; чем больше 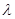, тем большей теплопроводностью обладает материал.

Величина коэффициента теплопроводности зависит от природы вещества, его структуры, влажности, наличия примесей, температуры и других факторов. Наибольший коэффициент теплопроводности имеют металлы и сплавы Изотермической поверхностью 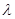7-420 .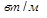

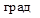Теплоизоляционные, керамические и строительные материалы обладают значительно меньшим коэффициентом теплопроводности - 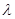- 0,023-2,9 .

В расчетах коэффициент теплопроводности строительных материалов следует принимать по СНиП П-3-79* «Строительная теплотехника».М ГП ЦПП 1995. Значения коэффициента теплопроводности приведены в таблице 1

Таблица 1

Материал	Коэффициент теплопроводности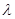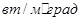
Бетон на гравии или щебне из природного камня	1,45
Керамзитобетон при плотности 1200 кг/м3	0,46
Грунт растительный под зданием	1,16
Кирпичная кладка из обыкновенного глиняного кирпича на легком растворе	0,76
Сложный раствор (песок, цемент, известь) или штукатурка из него	0,86
Алюминий
Сталь
Чугун
Вода (0-100 0С)	0,55-0,7
Лед	2,5
Воздух	0,024-0,075
Снег, уплотненный при плотности 350 кг/м3	0,35

1.4 ТЕПЛОПРОВОДНОСТЬ

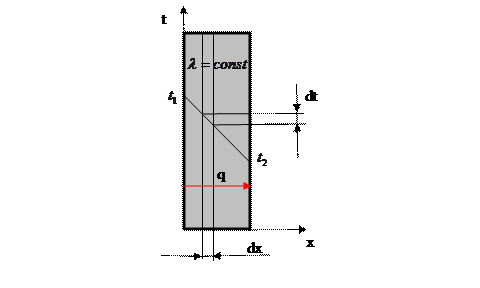
Рис.1.4.1.

Рассмотрим однослойную, плоскую стенку толщиной рис.1.4.1 Пусть коэффициент теплопроводности указанной стенки постоянен и равен 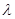. Температуры на границах стенки 1 и 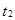, причем пусть 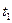меньше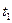. Тепло распространяется вдоль оси x. При этих условиях температурное поле в стенке будет одномерным и изотермическими поверхностями будут плоскости, параллельные поверхностям стенки.

Для слоя толщиной dx на основании закона Фурье можно написать следующие уравнения теплопроводности:

q=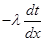 (1.4.1)

или

(1.4.2)

Проинтегрировав данное уравнение, получим

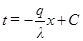(1.4.3)

Из уравнения следует, что температура изменяется по толщине стенки по закону линейному закону.

Константа интегрирования С определяется из условий на границах стенки: x=0, то 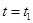. Если x=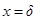, то 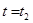и уравнение принимает вид

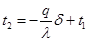(1.4.4)

Окончательно получим

(1.4.5)

Из уравнения видно, что удельный тепловой поток зависит от температурного перепада 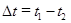, поэтому можно написать

(1.4.6.)

Или

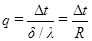(1.4.7)

Отношение называется термическим сопротивлением стенки. Зная удельный тепловой поток q, можно определить общее количество тепла, переданного в единицу времени через стенку площадью F, по формуле

(1.4.8).

Из формулы (1.4.8) видно, что общее количество тепла, переданного через однослойную, плоскую стенку, пропорционально удельному тепловому потоку и поверхности стенки F.

Рассмотрим теплопроводность плоской многослойной стенки, состоящей из трех слоев, прилегающих друг к другу. Каждый слой имеет заданную толщину 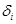и коэффициент теплопроводности 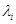(рис.3).

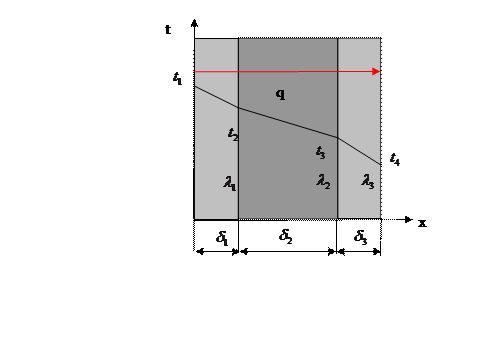
Рис.1.4.2

При стационарном тепловом режиме тепловые потоки через каждый из слоев стенки одинаковы. Пользуясь формулой (1.4.2) для каждого слоя можно написать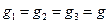

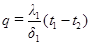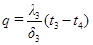; ; . (1.4.9)

Пренебрегая термическим сопротивлением контакта на границах раздела двух слоев, можно по этим уравнениям определить температуры поверхностей отдельных слоев, а также перепад температур в них:

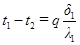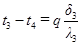; ; .(1.4.10)

Просуммировав, правые и левые части этих равенств, получим,

,

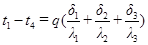откуда

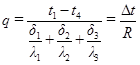(1.4.11),

где 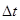- температурный перепад, т.е. разность температур наружных поверхностей стенки; R=R1+R2+R3+…Rn – общее термическое сопротивление многослойной стенки, равное сумме термических сопротивлений отдельных слоев.

Для построения температурного поля многослойной стенки необходимо знать температуру на поверхности каждого слоя в отдельности, которая определится из следующих равенств:

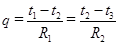и т.д. (1.4.12)

Температурное поле многослойной стенки будет представлять собой ломаную линию.

Тепловой поток через многослойную стенку определяется по формуле

(1.4.13).

Расчет теплопроводности однослойной и многослойной цилиндрической стенки можно производить по формулам для плоской стенки, если ее толщина незначительна (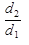 2) в этом случае, кривизна стенки незначительно влияет на величину теплового потока. В этом случае вместо F подсчитывается

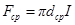(1.4.14)

где dср – средний диаметр цилиндра между наружной и внутренней поверхностями его стенки.

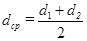.(1.4.15)

Более точное определение среднего диаметра производится по формуле

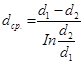(1.4.16).

1.5. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН

Конвективным теплообменом называют перенос теплоты массой жидкости (газа) нагретой или охлажденной у твердой поверхности. Направление теплового потока при этом будет зависеть от температур жидкости и стенки.

Различают естественную и вынужденную конвекцию. Естественная конвекция возникает в результате неоднородности теплового поля под действием внешних сил в частности гравитационных сил.

Вынужденная конвекция возникает в результате приложения к массе жидкости внешних сил (использование увеличении интенсивности движения насосов, вентиляторов и т.п.).

а).

б)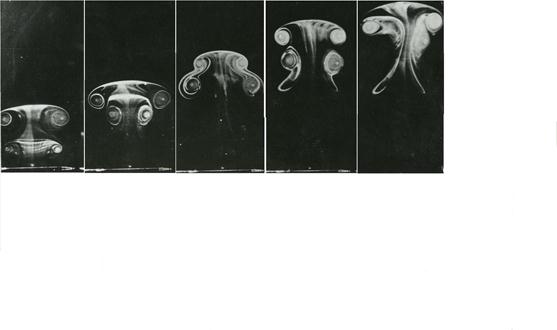

в)

Рис.1.5.5.

На рис.4 приведены снимки конвективного движения воздуха, а) и б) естественной конвекции, в) вынужденная конвекция.

Конвективный поток образованный рис.4а. 4б. «Сахара эффект», термики, «Грибообразные столбики» периодически поднимаются с протяженной нагретой пластины. Подтекание охлажденного воздуха происходит за счет опускания его сверху. Искусственная конвективная струя воздуха (рис. 4 в) образованная смешением двух нагретых струй подаваемых из оппозитных отверстий образованных полуцилиндрическим внутренним экраном.

Тепловой поток при конвективном теплообмене, определяется по формуле:

, (1.5.17)

где 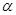- коэффициент теплоотдачи;

tж – температура теплоносителя в ;

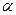- температура стенки в ;

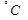F – поверхность соприкосновения теплоносителя со стенкой в м2.

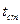- температура стенки

Из данного уравнения можно определить разность 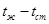и температуру стенки :

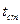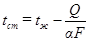- (1.5.18)

Формула справедлива как при конвективном теплообмене от жидкости к стенке, так и при конвективном теплообмене от стенки к жидкости.

Коэффициент теплоотдачи 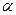представляет собой величину теплового потока. В отличие от коэффициента теплопроводности 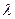коэффициент теплоотдачи 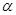- сложная величина. Он учитывает следующие факторы: режим течения жидкости (ламинарный или турбулентный); физические параметры жидкости (теплопроводность 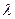, вязкость 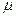, плотность 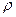, теплоемкость ср., коэффициент объемного расширения 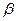), температуру жидкости и поверхности 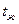, 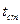; форму Ф и линейные размеры обтекаемой поверхности l.

Функционально такую зависимость можно выразить в виде:

(1.5.19)

Существенное значение при конвективном теплообмене имеет режим движения жидкости. При турбулентном движении теплообмен идет более интенсивно. При ламинарном движении менее интенсивно. Наличие пограничного слоя большой толщины у поверхности стенки увеличивает ее термическое сопротивление.

1.6 ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ

Теплообмен излучением представляет собой процесс взаимного облучения двух или нескольких тел виде электромагнитных волн. Этот вид теплообмена связан с взаимным превращением энергии: тепловой энергии в излучение и излучения в тепловую энергию. Интенсивность лучистого теплообмена увеличивается по мере повышения температуры тела, испускающего электромагнитные волны.

Лучистая энергия, попадая на какое-нибудь тело, частично поглощается этим телом, частично отражается и частично проходит через него. Энергия, поглощаемая телом, переходит в тепловую энергию.

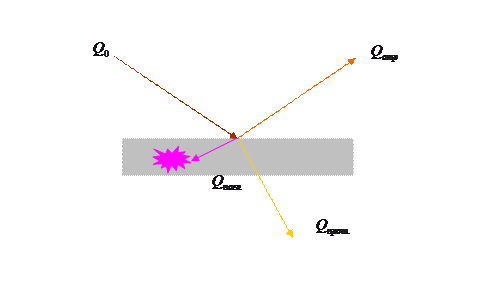
Рис.1.6.1.

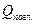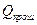Обозначая через Q0 общее количество излучаемой энергии, поступающей на тело, а через , и – соответственно количество лучистой энергии, поглощенной, отраженной и прошедшей через него:

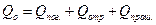. (1.6.1)

Записав уравнение (1.21) в относительном виде, получим

(1.6.2)

или

,

где - поглощательная способность тела;

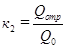- отражательная способность тела;

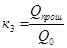- пропускная способность тела.

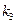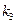Коэффициенты и являются безразмерными коэффициентами поглощения, отражения и пропускания. В зависимости от конкретных физических свойств тела, его температуры и длины волны падающего излучения численные значения коэффициентов и могут быть различными и равными нулю.

Если 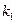=1 (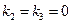), то тело полностью поглощает все падающие на него тепловые лучи и называется абсолютно черным.

Если (), то тело полностью отражает падающие на него тепловые лучи. Такое тело называют зеркальным (если отражение правильное, не рассеянное) либо абсолютно-белым (если отражение рассеянное – диффузное).

Если, 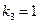(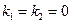), то тело пропускает через себя все падающие на него лучи. Такое тело называют абсолютно-проницаемым (прозрачным) или диатермичным. Воздух – практически прозрачная среда, твердые тела и жидкости непрозрачны. Многие тела прозрачны только для определенных волн. Так, оконное стекло пропускает световые лучи и почти непрозрачно для ультрафиолетового и длинноволнового инфракрасного излучения.

Основные законы лучистого теплообмена были открыты И. Стефаном и Л. Больцманом

Закон Стефана-Больцмана. И. Стефан экспериментально, а Л.Больцман теоретически установили связь излучения абсолютно черного тела Е0 с температурой. В технических расчетах закон Стефана-Больцмана используется в следующем виде:

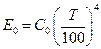, (1.6.3)

где С0 – коэффициент излучения абсолютно черного тела,

Существующие в природе тела, являются серыми, по интенсивности излучения отличаются от абсолютно черного тела. Однако закон Стефана-Больцмана применим и к серым телам, если ввести коэффициент степени черноты и учесть тем самым их степень черноты:

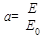, (1.6.4)

где а - коэффициент степени черноты

Е – способность излучения серого тела;

Е0 – излучения способность абсолютно черного тела.

Применительно к реальным телам закон Стефана-Больцмана имеет следующий вид:

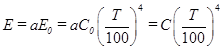, (1.6.5)

где С=аС0 – коэффициент излучения.

Величина степени черноты зависит от природы тела, температуры и состояния его поверхности.

По закону Ламберта устанавливается взаимосвязь между излучаемой телом энергии от ориентации. Максимальное излучение единицей поверхности происходит по направлению нормали.

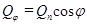. (1.6.6.)

Таким образом, закон Ламберта определяет зависимость излучаемой телом энергии от направления.

По закону Кирхгофа отношение способности излучения Е к его способности поглощения для всех тел одинаково и равно способности излучения абсолютно черного тела Е0 при той же температуре и зависит только от температуры, т.е.

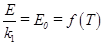(1.6.7)

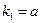Так как , то для всех серых тел , т.е. поглощательная способность тела численно равна его степени черноты.

В общем случае передаваемое тепло между излучаемыми поверхностями можно определить из выражения (1-28)

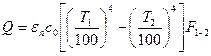, (1.6.8)

Где 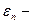коэффициент, приведенный степени черноты; 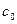-коэффициент излучения абсолютно черного тела; 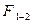-поверхность, лучистого взаимного теплообмена.

Интенсивность лучистого теплообмена между твердыми телами зависит от их температуры, конфигурации, размеров, состояния поверхностей, взаимного расположения и расстояния между ними.

Эффективным средством уменьшения интенсивности теплообмена служат различного рода защитные экраны.

При наличии экрана лучистое тепло передается от стенки к экрану, а от экрана к другой стенке.

Если материал экрана и стенки сходны по качеству и материалу, то экран уменьшит лучистый тепловой поток в 2 раза.

Если поверхность экрана имеет очень небольшой коэффициент поглощения и хорошо отражает лучистую энергию, никелированный или полированный алюминиевый лист, то один экран может уменьшить тепловой поток в 10-30 раз.

1.7 СЛОЖНЫЙ ТЕПЛООБМЕН

Сложный теплообмен включает теплопроводность, конвекция и тепловое излучение

В теплотехнических расчетах при сложном теплообмене, как правило, пользуются суммарным коэффициентом теплоотдачи 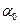. Указанный коэффициент представляет собой сумму коэффициентов конвективной теплоотдачи 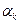и лучистой теплоотдачи ;

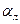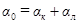(1.7.1)

В этом случае расчетная формула для теплообмена имеет вид

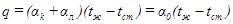(1.7.2)

При обмывании стенки капельной жидкостью указанный коэффициент будет равен 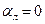и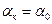

Сложный теплообмен включает все виды теплообмена Теплопередача от одной жидкости (или газа) к другой через стенку и представляет суммарный процесс теплообмена, в котором теплоотдача контактом является необходимой составной частью.

Теплопередача зависят от формы стенки, разделяющей теплоносители.

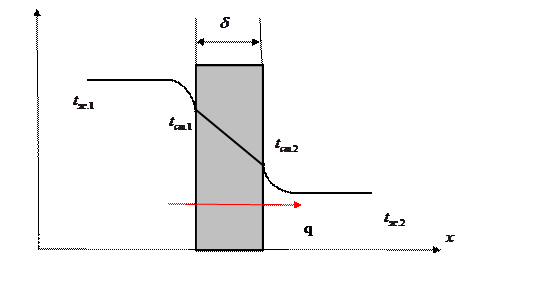
Рис.1.7.1.

Рассмотрим теплопередачу через плоскую однослойную стенку рис. 6. Примем, что тепловой поток направлен слева направо, температура нагретой среды tж.1, температура холодной среды tж.2. Температуры поверхностей стенки неизвестны, обозначим их буквами .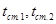

Передача тепла в данном случае представляет собой процесс сложного теплообмена и состоит из теплоотдачи от нагретой среды, теплопроводность через стенку и теплоотдача от стенки к холодной среде. При этом видно, что удельные тепловые потоки при трех видах одни и те же.

В этом случае уравнения теплового потока будут иметь вид:

Уравнение теплоотдачи от нагретой среды к поверхности стенки

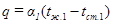. (1.7.3)

Уравнение теплопроводности через стенку

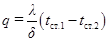(1.7.4)

Уравнение теплоотдачи к холодной среде

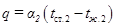. (1.7.5)

Сложив эти уравнения, получим полный температурный напор:

, (1.7.6)

откуда удельный тепловой поток

(1.7.7)

Величина 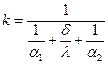называется коэффициентом теплопередачи и представляет собой мощность теплового потока, проходящего от более нагретой среды к менее нагретой через 1м2 поверхности стенки при разнице температур между средами 1.

Величина, обратная коэффициенту теплопередачи, называется термическим сопротивлением теплопередаче и обозначается R.

В этом случае имеем:

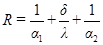(1.7.8)

В том случае если стенка многослойная, т.е. состоит из нескольких слоев - n с различной толщиной, а коэффициенты теплопроводности соответственно , то будем иметь

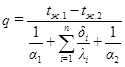, (1..7.9)

где 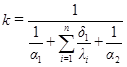, или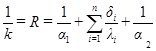

Количество тепла, переходящего через площадь F стенки за 1 час, будет равно:

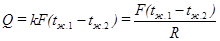(1.7.10)

Для расчета теплового потока при теплопередаче через многослойную цилиндрическую стенку можно воспользоваться выражением:

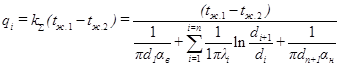(1.7.11)

1.8 ТЕПЛООБМЕННЫЕ АППАРАТЫ

Теплообменными аппаратами называются техническими устройства, назначение которых передача тепла от одного рабочего тела (теплоносителя) к другому. В качестве рабочего тела (теплоносителей) в них используют водяной пар, горячую воду, дымовые газы и другие тела.

По принципу действия и конструкции теплообменники разделяются на рекуперативные, регенеративные и смесительные.

Рекуперативные теплообменники передают тепло от нагретого теплоносителя к нагреваемой среде через разделяющую их стенку.

В зависимости от направления движения теплоносителей теплообменники указанного вида подразделяют - противоточные, прямоточные и перекрестные. Если теплоносители движутся в противоположном направлении, теплообменники называются противоточными (рис.7 б); при движении теплоносителей в одном направлении – прямоточными (рис.7 а), если теплоносители движутся в перекрестном направлении – перекрестными (рис.7 в).

В регенеративных теплообменниках поверхность нагрева представляет собой специальную насадку из профилированных колец, или других конструкций увеличивающих площадь контакта, которая сначала аккумулирует тепло, а затем отдает его нагреваемому теплоносителю.

В смесительных теплообменниках процесс теплообмена проходит при прямом контакте (соприкосновении и перемешивании) теплоносителей.

Рекуперативные и регенеративные теплообменники являются поверхностными теплообменными аппаратами, а смесительные теплообменники контактным.

Рис.1.8.1.

В зависимости от вида течения в теплообменнике (прямоток или противоток) расходов греющей и нагреваемой жидкости имеем четыре процесса теплообмена вдоль поверхности теплопередачи (рис. 8).

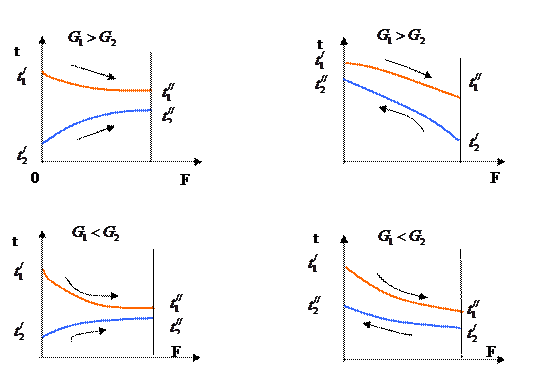
Рис.1.8.2.

Ниже рассматриваются основы расчета лишь рекуперативных теплообменников, как наиболее распространенных.

При конструктивном расчете теплообменника рабочая поверхность его определяется из уравнения теплопередачи

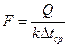(1.8.1),

где Q – мощность теплового потока, заданная потребителем тепла;

- коэффициент теплопередачи;

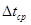- средний температурный напор по всей поверхности нагрева.

Значение коэффициента теплопередачи для цилиндрической поверхности определяются из выражения:

, (1.8.2.)

где - внутренний и наружный диаметр трубки через стенки которой идет теплообмен.

Величина среднего температурного напора определяется по формуле

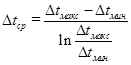(1.8.3),

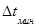где и - максимальная и минимальная разности температур

Для прямотока

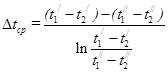(1.8.4);

Для противотока

, (1.8.5.).

где 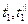-температура греющей среды, соответственно на входе и выходе в теплообменник; 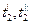-температура нагреваемой среды, соответственно на входе и выходе в теплообменник.

Выше приведенные формулы (1.41) и (1.42) позволяют оценить температурные напоры в теплообменниках с противоточной и прямоточной схемой движения теплоносителей. При прочих одинаковых параметрах теплоносителей на входе и выходе в теплообменник в противоточном теплообменнике средний температурный напор получается - наибольшим, а в прямоточном – наименьшим. Вследствие большой величины среднего температурного напора поверхность нагрева при противоточной схеме движения теплоносителей и прочих равных условиях будет наименьшей.

Расчет теплообменника производится по его тепловому балансу:

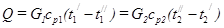, (1.8.6)

где 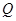- мощность теплового потока, переданного от греющего теплоносителя к нагреваемой среде;

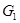и 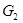- расходы теплоносителе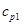й;

и - средние теплоемкости.

2. ГИДРАВЛИКА

2.1 ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ

Жидкость. Изучение основных законов механики жидкости (газов) необходимо начинать с особенностей различия свойств жидкостей и твердых тел.

Жидкость отличаются от твердых тел отсутсвием «твердой кристаллической решетки» и значительной свободой подвижности молекул. Изменение принятой формы жидкости происходит под действием даже при приложении самых малых сил (например, жидкость течет под действием собственного веса).

Жидкость имеет молекулярное строение - состоит из молекул, т.е. жидкость, имеет прерывистую структуру. В механики жидкости для простоты решения большинства задач принимают жидкость как сплошную (непрерывную) среду. Таким образом, вместо реальной физической субстанции самой жидкости изучается ее модель, обладающая свойством непрерывности (гипотетически сплошная среда). Введение аксиомы о непрерывности упрощает создание математического аппарата, описывающего состояния жидкости.

По своим физическим свойствам жидкость можно условно разделять на два состояния мало сжимаемые (капельные) и сжимаемые (газообразные).

Капельные жидкости обладают определенным объемом, который, например, изменяется под действием определенных сил. Газы, занимают все пространство и могут значительно изменять объем, сжимаясь и расширяясь под воздействием определенных сил.

Плотность жидкости. Плотностью жидкости 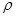, называется масса М, заключенная в единице объема W:

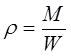(2.1.1)

Например, плотность воды при температуре 4° С .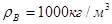

Удельный вес. Вес жидкости G, приходящийся на единицу объема W называется удельным вес

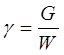(2.1.2)

Удельный вес воды при температуре 4°С .

Плотность и удельный вес жидкости связаны между собой соотношением

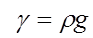(2.1.3)

где g — ускорение свободного падения.

Сжимаемость жидкостей. Сжимаемость капельных жидкостей под действием давления характеризуется коэффициентом объемного сжатия , который представляет собой относительное изменение объема жидкости на единицу изменения давления:

(2.1.4)

где W—первоначальный объем жидкости; dW—изменение этого объема при увеличении давления на величину dр.

Коэффициент объемного сжатия имеет размерность Па-1. Знак «минус» в формуле (4) обусловлен тем, что положительному приращению давления соответствует отрицательное приращение (т. е. уменьшение) объема жидкости W. Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкости Е0, Па:

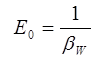(2.1.5)

Температурное расширение жидкостей. Температурное расширение капельных жидкостей характеризуется коэффициентом температурного расширения 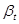, выражающим относительное увеличение объема жидкости при увеличении температуры на 1 град, т. е.

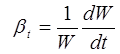,.(2.1.6)

где dW—изменение этого объема при повышении температуры на величину dt.

Газы характеризуются значительной сжимаемостью и высокими значениями коэффициента температурного расширения. Зависимость плотности газов от давления и температуры устанавливается уравнением состояния.

Наиболее простыми свойствами обладает газ, разрешенный настолько, что взаимодействие между его молекулами может не учитываться, так называемый идеальный газ. Для идеальных газов справедливо уравнение ’’Клайперона’’, позволяющее определять плотность газа при известных значениях давления и температуры:

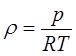, (2.1.7)

где р—абсолютное давление, R—удельная газовая постоянная, различная для разных газов, но не зависящая от температуры и давления [для воздуха R = 287 Дж/(кг·К)]; Т—абсолютная температура.

Поведение реальных газов в условиях, далеких от сжижения, незначительно отличается от поведения идеальных газов.

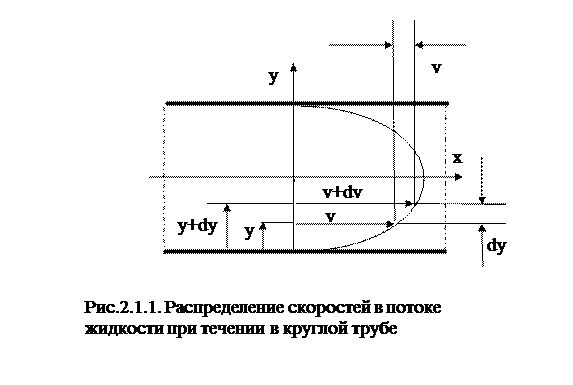
Вязкость жидкостей. Вязкостью называется свойство жидкостей оказывать сопротивление сдвигу. Все реальные жидкости обладают определенной вязкостью, которая проявляется в виде внутреннего трения при относительном перемещении смежных частиц жидкости.

Если рассматривать течение жидкости параллельными слоями (рис. 1) то можно предположить зависимость между напряжением деформацией в виде:

(2.1.8)

Величина 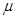называется коэффициентом динамической вязкости.

Сила внутреннего трения в жидкости может быть определена из выражения

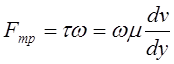, (2.1.9)

где 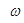площадь трения.

Трение в жидкости отличается от трения в твердых телах, где сила трения зависит от нормального давления и не зависит от площади трущихся поверхностей.

Вязкость жидкостей в большой степени зависит от температуры, при этом вязкость капельных жидкостей при увеличении температуры уменьшается, а вязкость газов возрастает.

В гидравлике находит применение понятие кинематической вязкости v, представляющей собой отношение динамической вязкости жидкости к ее плотности:

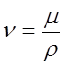(2.1.10)

Эта вязкость названа кинематической, так как в ее размерности отсутствуют единицы силы или массы.

2.2 Аномальные жидкости.

В природе, кроме обычных, так называемых “Ньютоновских жидкостей” существуют аномальные “Неньютоновские жидкости”. К этим жидкостям относятся некоторые смазочные масла, краски, суспензии, коллоидные растворы, жидкие полимеры, строительные растворы и т.д..

К числу аномальных жидкостей относятся также феррожидкости, ферромагнитные, электрореологические, переохлажденные (жидкости типа смол). Как правило, такие жидкости в определенных условиях имеют упругие деформации, а в других условиях вязкие деформации при их течение.

Жидкости с нелинейной «кривой течения» можно разбить на три обширные группы:

1.Системы, для которых скорость сдвига в каждой точке представляет некоторую функцию только напряжения сдвига в той же точке.

2. Более сложные системы, в которых связь между напряжением и скоростью сдвига зависит от времени действия напряжения или от «предыстории» жидкости.

3.Системы, обладающие свойствами, как твердого тела, так и жидкости и частично проявляющие упругое восстановление формы после снятия напряжения (так называемые вязкоупругие жидкости).

2.2.1. Неньютоновские жидкости с реологическими характеристиками, не зависящими от времени.

Системы первого типа, свойства которых, не зависят от времени, могут быть описаны реологическим уравнением. Из которого следует, что скорость сдвига в каждой точке жидкости является простой функцией напряжения сдвига в той же точке. Такие вещества могут быть названы неньютоновскими вязкими жидкостями. Они подразделяются на три группы

а) бингамовские пластичные жидкости

б) псевдопластичные жидкости

г) дилатантные жидкости

Кривые течения, характерные для этих трех групп жидкостей, приведены на рис.2; для сравнения так же дан график линейной зависимости для ньютоновских жидкостей.

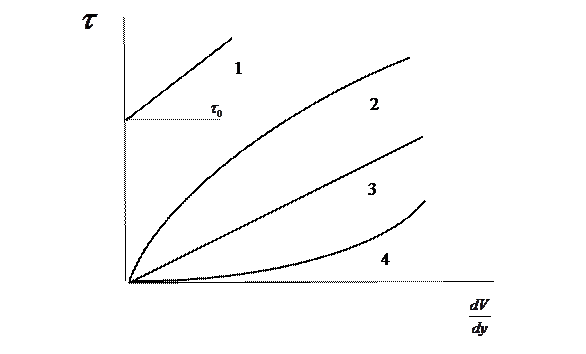
Рис. 2.2.1 Кривые течения для различных типов

реологически стационарных неньютоновских

жидкостей.

1 – бингамовский пластик; 2 – псевдопластичная;

3 – ньютоновская жидкость; 4 – дилатантная.

Бингамовские пластики. Псевдопластики. Дилатантные жидкости. Бингамовские пластики (рис.2.2.1 линия 1) «Кривая течения» для этих материалов представляет прямую линию, пересекающую ось напряжения сдвига на расстоянии от ее начала. Напряжение текучести есть предел, превышение которого приводит к возникновению вязкого течения (рис.2.2.1)

Псевдопластики. Псевдопластичные жидкости (рис.2.2.1 кривая-2) не обнаруживают предела текучести, а кривая течения у них показывает, что отношение напряжения сдвига к скорости сдвига, т.е. кажущаяся вязкость, постепенно понижается с ростом скорости сдвига. Кривая течения становится линейной только при очень больших по величине скоростях деформации сдвига. Предельный наклон графика, получивший название вязкости при бесконечно большом сдвиге.

График зависимости между напряжением сдвига и его скоростью в логарифмических координатах у псевдопластичных материалов зачастую оказывается линейным с тангенсом угла наклона в пределах между нулем и единицей.

Дилатантные жидкости. Такие жидкости сходны с псевдопластиками тем, что в них так же отсутствует предел текучести, однако их кажущаяся вязкость повышается с возрастанием скорости сдвига (рис.2.2.1. кривая 4)

Неньютоновские жидкости, реологические характеристики которых зависят от времени. Кажущаяся вязкость более сложных жидкостей определяется не только скоростью сдвига, но и продолжительностью сдвига. Эти жидкости в соответствии с тем, убывают или возрастают со временем напряжения сдвига, если жидкость деформируется с постоянной скоростью сдвига, можно подразделить на два класса: а) тиксотропные и б) реопектические.

2.2.2 Тиксотропные жидкости. Реопектические жидкости. Вязкоупругие жидкости.

Тиксотропные жидкости. Это материалы, консистенция которых зависит от продолжительности сдвига и величины скорости сдвига.

Реопектические жидкости. Данным материалам свойственно постепенное структурообразование при сдвиге, тогда как до сих пор свойства структурированных систем объяснялись исходя из того, что сдвиг способствует разрушению структуры.

Вязкоупругие жидкости. Вязкоупругим называется материал, проявляющий как упругое восстановление формы, так и вязкое течение. Примером таких жидкостей являются смолы. В таких структурах вязкая составляющая характеризуется законом Ньютона, а упругая подчиняется закону Гука. Причем параметр времени является постоянной времени экспоненциального ослабления напряжения при неизменной деформации, т.е. напряжение после прекращения движения будет уменьшаться т.н. релаксация времени.

Вязкость растворов ВМС. По характеру вязкого течения жидкостные дисперсные системы делятся на две группы:

1) бесструктурные системы, частицы которых более или менее свободны и почти не взаимодействуют друг с другом (растворы низкомолекулярных веществ, разбавленные эмульсии, суспензии и золи);

2) структурированные системы — содержат частицы, взаимодействующие друг с другом и с дисперсионной средой (растворы ВМС, концентрированные эмульсии и суспензии).

.Зависимость вязкости от скорости течения наблюдается у концентрированных эмульсий и суспензий с палочкообразной, эллипсоидной или пластинчатой формами частиц. Капельки дисперсной фазы в эмульсиях с возрастанием приложенного давления и увеличением скорости истечения удлиняются, превращаясь из шариков в эллипсоиды. Это облегчает истечение и ведет к понижению вязкости.

2.2.3 Вязкость рассолов

Концентрированные растворы солей. Исследования концентрированных растворов солей, образующих кристаллогидраты, с помощью криоскопических измерений, измерения вязкости, электропроводности и спектров поглощения показывают, что в таких растворах часть молекул воды включается в образование сложных гидратов и не присутствует в растворе как растворенные.

На графике (рис 2.2.3.) представлена зависимость динамической вязкости исследуемых рассолов от их минерализации. В данном случае под слабо минерализацией рассматривается - минеральный состав с pH 6,5- 8.8, при общей минерализации 200-500 мг/л. При большей минерализации растворы можно отнести к концентрированным рассолам. В области малых концентраций изменение вязкости происходит незначительно, так как здесь еще существует первичная структура воды и самостоятельная структура гидратных сфер ионов. С ростом минерализации соотношение меняется и преобладающей становится структура гидратированных ионов, что на ГПГ (граница полной гидратации - ГПГ) выражается в существовании физико-химической системы, где все ионы однослойно гидратированы и сближены на расстояния, составляющие в среднем 0,467±0,08 нм, а структура воды, как свободная фаза исчезает.

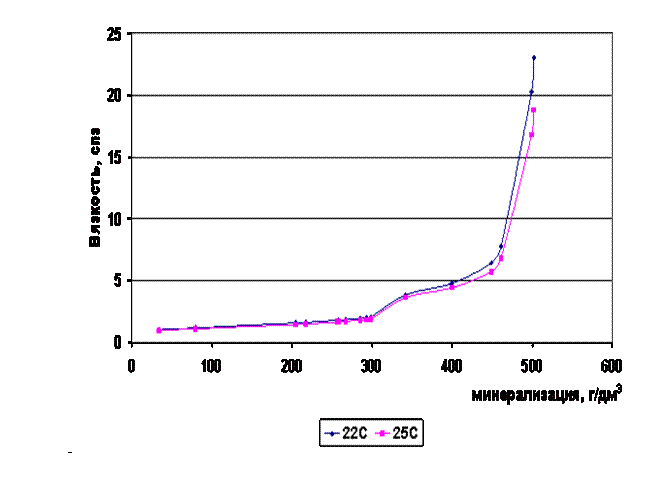
Рис 2.2.3. Зависимость вязкости рассолов от минерализации и температуры

Можно отметить две области минерализаций, после которых значение вязкости начинает резко возрастать. Первая область характерна для рассолов с минерализацией 320-340 г/дм3. Во второй области (450-550 г/дм3) происходит резкое, скачкообразное повышение вязкости. Следовательно, в рассолах данных диапазонов минерализаций следует ожидать максимумы электропроводности. В соответственных областях минерализаций структура раствора переходит из области, где существует структура воды, в область, в которой ближняя упорядо­ченность раствора соответствует структуре кристаллогидрата. За ГПГ, на фоне нарастающего дефицита воды (см. рис. 2.2.3), начинается координационная дегидратация, состоящая в перераспределении молекул воды гидратных оболочек в пользу наиболее гидрофильных ионов, что и проявляется в резком изменении свойств рассолов.

Знание форм нахождения ионов в рассолах, определенное на основании гидрохимических расчетов и сравнение их процентного соотношения и степени гидрофильности (как простых ионов, так и комплексных форм) позволяет предсказать степень их гидрофильности, а соответственно, способность выделяться в различных технологических процессах.

2.2.4 Ферромагнитные жидкости.

Феррожидкости. Феррожидкости представляют собой искусственно синтезированную устойчивую коллоидную взвесь, состоящую из магнитных наночастиц (диаметром примерно 10 нм), поверхностно активного вещества (сурфактанта), препятствующего слипанию частиц, и жидкого носителя: его роль могут исполнять вода, керосин или другой органический раствор. Пока магнитное поле отсутствует, феррожидкость ничем не отличается от обычной вязкой жидкости, а ориентация магнитных частиц имеет случайный, произвольный характер. Попадая в магнитное поле, частицы сразу выстраиваются вдоль силовых линий и создают своего рода объемный слепок. Меняя свойства и интенсивность магнитного поля, можно формировать из жидкости фигуры. Они считаются весьма перспективным классом наноматериалов и применяются, например, в качестве смазки в подшипниках скольжения, обеспечивая минимальное трение в узлах таких устройств, как, например, приводы магнитных и оптических дисков.

Магнитные свойства магнитных жидкостей определяется объемным содержанием твердой фазы, которое может достигать 25%. Намагниченность насыщения таких концентрированных магнитных жидкостей достигает 100 кА/м2 в магнитных полях напряженностью А/м2 при сохранении текучести. Магнитная восприимчивость таких жидкостей на несколько порядков больше, чем у однородных парамагнитных жидкостей. Наиболее распространенной магнитной жидкостью является магнитная жидкость на основе керосина с дисперсными магнетитовыми частицами с олеиновой кислотой в качестве стабилизатора.

Вследствие возможности локализации магнитных жидкостей полем были разработаны магнитожидкостные уплотнения, управляемые смазочные материалы, магниточувствительные жидкости для дефектоскопии и т.п. На практике применяются самые разнообразные магнитные жидкости, среди которых следует особо выделить жидкости на основе минеральных масел и кремнийорганических сред. Вязкость таких магнитных жидкостей при намагниченности насыщения до 60 кА/м2 может достигать значительных величин, поэтому их иногда сравнивают с магнитными пастами. Для нужд медицины разрабатываются магнитные жидкости на различных пищевых растительных маслах. Ферромагнитные жидкости используются для создания жидких уплотнительных устройств вокруг вращающихся осей в жестких дисках. Вращающаяся ось окружена магнитом, в зазор между магнитом и осью помещено небольшое количество феррожидкости, которая удерживается притяжением магнита. Жидкость образует барьер, препятствующий попаданию частиц извне внутрь жесткого диска.

Ферромагнитная жидкость способна снижать трение. Нанесенная на поверхность достаточно сильного магнита, например неодимового, она позволяет магниту скользить по гладкой поверхности с минимальным сопротивлением.

.2.3 ОСНОВЫ ГИДРОСТАТИКИ

2.3.1 РАВНОВЕСИЕ ЖИДКОСТИ

Действующие силы и равновесное состояние жидкости. Рассмотрим некоторый объем жидкости рис.2.3.1

Рассматриваемый объем жидкости находится в состоянии относительного равновесия. В этом случае выделенная точка М также находится в состоянии равновесия. Такое состояние предполагает равновесное состояние сил, воздействующих на выделенный объем.

Рис. 2.3.1.

На выделенный объем действуют внешние силы – поверхностные и объемные силы. Объемные силы – это внешние силы пропорциональные объему и плотности вещества. Поверхностные силы – силы, действующие в границах выделенного объема. Условие равновесия предполагает присутствие нормальной составляющей N и касательной составляющей K. Касательная составляющая К для условия относительного равновесия должна бать равна нулю. Таким образом, условие относительного равновесия в рассматриваемом случае предполагает равенство поверхностных и объемных сил.

Поверхностные силы. Поверхностные силы определяют так называемое поверхностное «напряжение». Поверхностное напряжение определяется выражением:

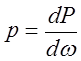, (2.3.1)

где Р - действующая поверхностная сила, 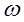- площадь взаимодействия поверхностной силы.

Объемные силы. Объемные силы (массовые силы) определяются воздействие внешних сил. Для них можно записать:

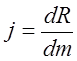(3.3.2)

2.3.2 Основная теорема гидростатики

Основная теорема гидростатики. Основная теорема гидростатики устанавливает то, что гидростатическое дав

Дата добавления: 2014-10-15