Основные понятия и определения

Определение. Всякий ненулевойминор матрицы А, порядок которого равен рангу матрицы называется базисным минором.

В последнем 4-м примере 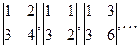- базисные, т.к. ¹0 и s= r(A)=2. Минор 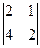=0 не является базисным.

Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными.

В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.

В курсе алгебры важную роль играет теорема о базисном миноре, которую мы приведем без доказательства:

Теорема о базисном миноре.

Теорема. В произвольной матрице А каждый столбец (строка) является линейной комбинацией ее базисных столбцов (строк).

Таким образом, ранг произвольной матрицы А равен максимальному числу линейно независимых строк (столбцов) в матрице.

Если А- квадратная матрица и D(A) = 0, то по крайней мере один из столбцов – линейная комбинация остальных столбцов. То же самое справедливо и для строк. Данное утверждение следует из свойства линейной зависимости при определителе равном нулю.

ГЛАВА 3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.

Система m линейных уравнений с n неизвестными имеет вид:

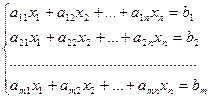(1.1),

где a_ij, b_i – произвольные числа, называемые соответственно коэффициентами и свободными членами уравнений.

В более краткой записи с помощью знаков суммирования систему можно записать в виде:

(1.2).

Решением системы являются n чисел (х₁=a₁, х₂=a₂… х_n=a_n), при подстановке которых в систему каждое ее уравнение обращается в тождество.

Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.

Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.

Определение. Для системы линейных уравнений матрица

А = называется матрицей системы, а матрица

А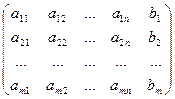^*= называется расширенной матрицей системы.

Две системы уравнений называются равносильными (эквивалентными), если они имеют одно и то же множество решений. С помощью элементарных преобразований системы уравнений, рассмотренных в гл.2 применительно к матрицам (например, умножение обеих частей уравнений на числа, не равные нулю; сложение уравнений системы), получается система, равносильная данной.

Систему (1.1) можно записать в матричной форме:

А=, Х = , В=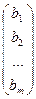, где А – матрица коэффициентов при переменных (матрица системы); Х – матрица-столбец переменных; В- матрица-столбец свободных членов. Тогда систему (1.1) можно записать в виде: АХ = В.

Дата добавления: 2014-10-31