Многогранники

8.4.1. Проекции призмы.

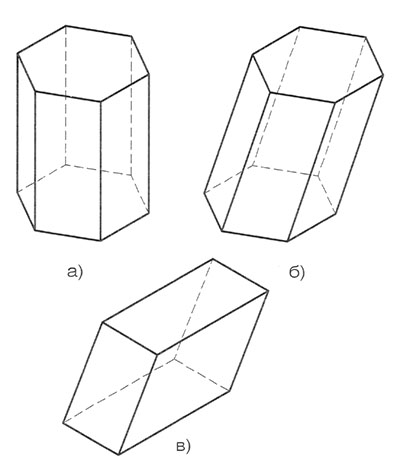
Призма (греч. Prisma), многогранник, две грани которого (основания) - равные многоугольники, расположенные в параллельных плоскостях, а другие грани (боковые) - параллелограммы. (Рис. 71). По числу боковых граней призмы разделяются на трехгранные, четырехгранные и т.д. Призма, основания которой параллелограммы, называется параллелепипедом. (Рис.71 в) Если все боковые грани составляют с основаниями прямые углы, призма называется прямой. (Рис.71 а)

Рис. 71

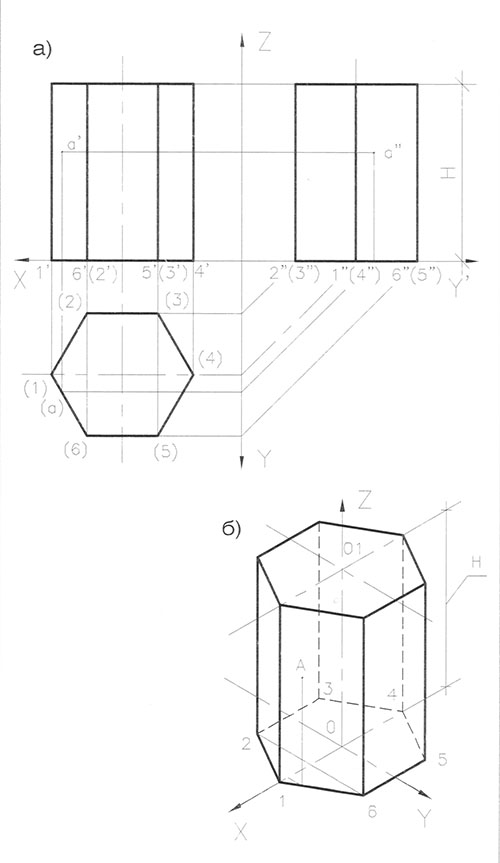
Построение ортогональных проекций прямой шестигранной призмы приведено на рис. 72а. Горизонтальная проекция призмы представляет правильный шестигранник. На фронтальную и профильную проекции призма проецируется в виде прямоугольников, ширина которых определяется горизонтальной проекцией, а высота равна высоте призмы. Вертикальные стороны прямоугольников - проекции вертикальных граней боковой поверхности призмы.

Рис. 72

Построение призмы в прямоугольной изометрии приведено на рис.726. Построение начинаем с расположения аксонометрических осей OX, OY, OZ, проведя их под углом 120° друг к другу. Ось призмы направим по оси OZ и отложим на ней высоту призмы. Через точку О1прве-дем аксонометрические оси 01X1 параллельно ОХ и 01Y1 параллельно 0Y.. Принимая точки О и 01 за центры верхнего и нижнего оснований призмы, строим два одинаковых шестигранника, основания призмы. Затем соединяем вершины нижнего и верхнего оснований вертикальными ребрами. Невидимую часть нижнего основания призмы и задние (невидимые) ребра выполним штриховой линией.

Построение точек на поверхности призмы в ортогональных и аксонометрической проекциях показано на рис.72. Точка А расположена на боковой поверхности призмы. По ее фронтальной проекции а' находим ее горизонтальную проекцию (а), лежащую на шестиграннике основания призмы. Профильная проекция (а") точки А строится обычным способом нахождения ее координат (ах, ау, az) по осям. На прямоугольной изометрии цилиндра точка А также строится обычным способом по ее координатам (ах, ay, az).

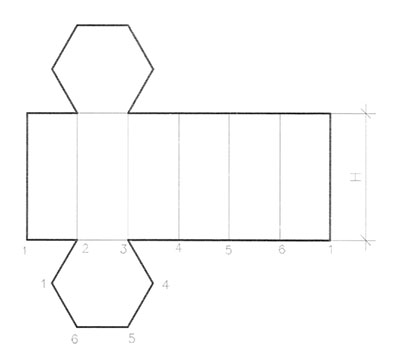
Построение развертки поверхности призмы показано на рис.73. Разверткой поверхности называют плоскую фигуру, образуемую последовательным совмещением плоских элементов этой поверхности с одной плоскостью.

Рис. 73

Размеры всех элементов развертки имеют натуральную величину.

Полная поверхность призмы состоит из боковой поверхности и двух равных оснований (верхнего и нижнего). Боковая поверхность призмы представляет собой шесть прямоугольников с основанием равным стороне правильного шестигранника и высотой, равной высоте призмы. Для получения полной развертки призмы необходимо к развертке боковой поверхности пристроить верхнее и нижнее основания.

Для перенесения на развертку точки А, принадлежащей боковой поверхности призмы, на ребре 1-6 развертки откладывают расстояние (1)-(а), взятое с плана призмы (Рис.72а), и через полученную точку К восставляют перпендикуляр к ребру 1-6, длина которого равна высоте точки А, взятой с фронтальной проекции (Рис.72а).

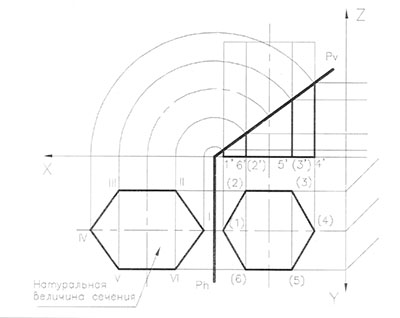
Построение сечения призмы наклонной секущей плоскостью Р, перпендикулярной фронтальной плоскости проекции, показано на рис.74. В данном случае сечение получается в виде шестиугольника на профильной проекции, фронтальная проекция которого совпадает со следом секущей плоскости Pv, а горизонтальная - с горизонтальной проекцией призмы.

Для построения прямоугольной изометрии усеченной призмы высота вертикальных ребер принимается равной их действительному значению, взятому с фронтальной или профильной проекций. (Рис.746).

Рис. 74

Натуральная величина сечения (I - XI) получена методом совмещения секущей плоскости с плоскостью Н. Указанные точки шестиугольника находят путем пересечения боковых ребер с заданной плоскостью. (Рис.75).

Рис. 75

При построении развертки усеченной призмы необходимо высоту вертикальных ребер откладывать в соответствии с их натуральной величиной, взятой с фронтальной или профильной проекций, а верхним основанием, в этом случае, является натуральная величина сечения.

Практические занятия по теме «Призма».

Упражнение 1. Вычертить ортогональные проекции прямой шестигранной призмы с заданными размерами и ее аксонометрическое изображение в прямоугольной изометрии.

Упражнение 2. Построить проекции точек на видимой и невидимой частях поверхности призмы на ортогональном и аксонометрическом изображении.

Упражнение 3. Вычертить ортогональные проекции усеченной прямой шестигранной призмы с заданными размерами и ее аксонометрическое изображение в прямоугольной изометрии.

Упражнение 4. Построить развертки целой и усеченной призмы под произвольными углами.

Цель задания. Изучить особенности построения прямой шестигранной призмы в ортогональных проекциях и в аксонометрии.

Методические указания. После выполнения простых упражнений могут решаться более сложные задачи по усмотрению преподавателей.

8.4.2. Проекции пирамиды.

Пирамида (греч. Pyramis) - многогранник, основание которого многоугольник, а остальные грани -треугольники, имеющие общую вершину. По числу углов основания различают призмы треугольные, четырехугольные и д.т. (Рис.76).

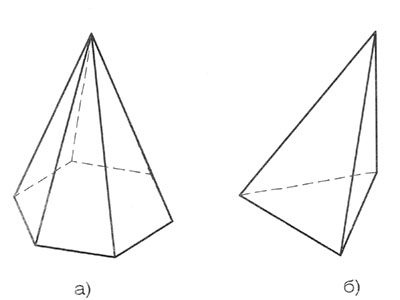
Рис. 76

Построение ортогональных проекций правильной трехгранной пирамиды приведено на рис.77а. Горизонтальная проекция пирамиды представляет правильный треугольник основания вершины которого соединены с вершиной пирамиды. На фронтальную проекцию пирамида проецируется в виде двух треугольников, а на профильную - в виде одного треугольника. Наклонные стороны треугольников - проекции боковых ребер пирамиды.

Рис. 77а

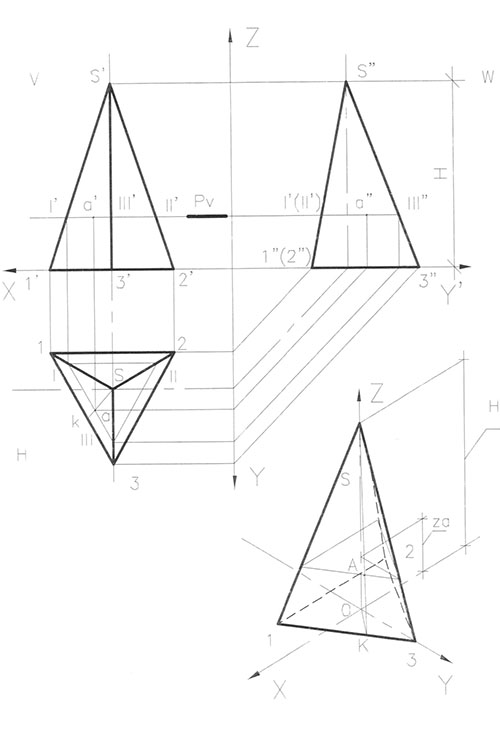
Построение точек на поверхности пирамиды в ортогональных и аксонометрической проекциях показано на рис.77.

Если на фронтальной проекции пирамиды задана точка А, то недостающие проекции этой точки можно построить двумя способами.

Первый способ: с помощью проекций вспомогательной линии s'k', проходящей через заданную точку. (Рис.77а).

Дано: фронтальная проекция точки А - точка (а'), расположенная в пределах видимой части пирамиды.

Через вершину пирамиды и заданную точку (а') проводим прямую линию до ее основания и получаем точку (к') - прямая s'k'.

Далее строим горизонтальную проекцию этой прямой на плоскости Н. Найдем горизонтальную проекцию этой прямой, проведя проецирующую прямую k'k, и соединим полученную т. к с горизонтальной проекцией вершины пирамиды s.

Так как искомая т. А принадлежит прямой s'k' то она должна лежать на ее горизонтальной проекции. Поэтому с помощью линии связи мы переносим ее на линию sk и получаем горизонтальную проекцию т. а.

Профильная проекция а" т. А определяется пересечением той же прямой s"k" на профильной проекции с линиями связи, переносящими т. а фронтальной проекций.

Второй способ: с помощью построения проекции сечения пирамиды горизонтальной плоскостью Pv параллельной основанию пирамиды и проходящей через заданную точку А. (Рис.776).

Рис. 77б

Дано: фронтальная проекция точки А-т. а', расположенная в пределах видимой части пирамиды.

Через т. а' проводим прямую, Pv параллельную основанию пирамиды, которая является фронтальной проекцией секущей плоскости Р. Эта линия пересекает боковые ребра пирамиды sT, s'2', s'3' в точках Г, 1Г и ИГ соответственно. Построив горизонтальные проекции этих точек на боковых ребрах пирамиды и соединив их линиями построения, получим горизонтальную проекцию сечения пирамиды плоскостью Pv. Отрезок прямой ПГ является фронтальной проекцией сечения пирамиды через точку а'.

Горизонтальной проекцией этого сечения будет треугольник, стороны которого параллельны основанию пирамиды.

Так как точка а' лежит в плоскости сечения, то с помощью линии связи переносим ее на горизонтальную проекцию сечения.

Профильная проекция т. а" определяется как пересечение профильной проекции сечения ГИГ с линией связи, переносящей положение т. а с горизонтальной проекции.

Построение точек на поверхности пирамиды в аксонометрии.

Строим пирамиду в прямоугольной изометрии. Построение начинаем с треугольного основания пирамиды и, отложив на вертикальной оси высоту пирамиды, проводим три боковых ребра, причем невидимое ребро проводим штриховой линией. (Рис.77).

Первый способ. Рис.77а.

Строим образующую SK: на оси X или Y откладываем координаты X или Y, соответствующие т. К на горизонтальной проекции, и проведем через них линии, параллельные оси Y или X соответственно. Пересечение их с основанием пирамиды дает положение точки К.

Соединим т. К с вершиной пирамиды S и с центром основания т. 0. Рассмотрим полученный треугольник S0K: сторона OS - вертикальная ось пирамиды, совпадающая с осью Z. Сторона SK - прямая, на которой находится т. А. Сторона 0К - основание треугольника составляющая с осью Z угол 90°.

Высоту т. А берем на фронтальной проекции по перпендикуляру от основания пирамиды до т. а' и откладываем ее в аксонометрии на оси Z, то есть на стороне OS.

Через полученную засечку проводим прямую в плоскости треугольника параллельно основанию треугольника до пересечения с прямой SK.

Таким образом, переносим высоту положения т. А на поверхность пирамиды.

Второй способ. Рис.776.

Строим сечение пирамиды плоскостью, параллельной основанию и проходящей через т. А. Такое сечение пирамиды есть треугольник, подобный основанию пирамиды, расположенной на высоте, равной высоте т. A (za). Отложим величину za, взятую с фронтальной проекции по оси Z на аксонометрии и через полученную засечку проведем линию, параллельную оси Y до пересечения с ребром S3 - т. III. Далее через т. Ill проводим линии параллельные основанию пирамиды (31 и 32) до пересечения с соответствующими боковыми ребрами S1 и S2, получив линию сечения пирамиды горизонтальной плоскостью Pv в аксонометрии. На горизонтальной проекции пирамиды проведем прямую SK через горизонтальную проекцию т. А и найдем положение т. К на аксонометрии. Проведем на аксонометрии пирамиды прямую SK. Ее пересечение с линией сечения пирамиды даст положение искомой т. А на аксонометрии.

Использование первого или второго способа построения недостающих проекций т. А определяется ее положением в каждом конкретном случае. Так как проекции точек определяются пересечением линий построения, то точность построений тем выше, чем ближе угол между пересекающимися прямыми к 90°. Если прямая SK, на которой лежит т. А, составляет с осями координат X и Y 45°, то определить положение т. А на аксонометрии первым способом вообще невозможно.

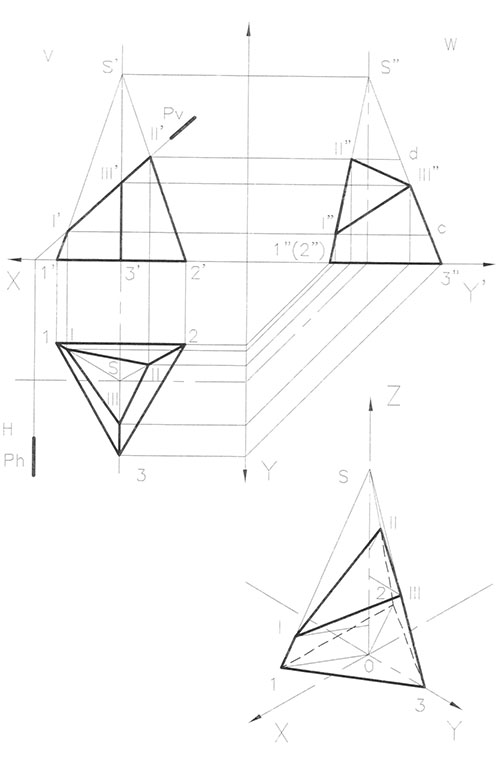
Построение усеченной пирамиды. (Рис.78).

Рис. 78

Строим три проекции пирамиды - горизонтальную. фронтальную и профильную, (см. выше).

На фронтальной проекции пирамиды проводив линию секущей плоскости Pv под произвольным углом к основанию пирамиды и обозначаем римскими цифрами точки пересечения наклонных ребер пирамиды с секущей плоскостью (т. Г, II', III").

Переносим эти точки на горизонтальную проекцию пирамиды (I, II, III) и, соединив их, получаем горизонтальную проекцию сечения.

Затем строим профильную проекцию сечения пирамиды, находя положение точек I", II" и III".

Построение аксонометрии усеченной пирамиды. Рис. 78. Строим аксонометрическую проекцию пирамиды, как описано выше.

Далее переносим точки 1, II и III с фронтальной проекции на аксонометрию. Откладываем на аксонометрии по оси Z высоту точки I, взятую с фронтальной проекции, и через полученную точку проведем линию, параллельную прямой 01 до пересечения с ребром S1. Данное пересечения определяет положение т. I. Остальные точки строим аналогичным способом.

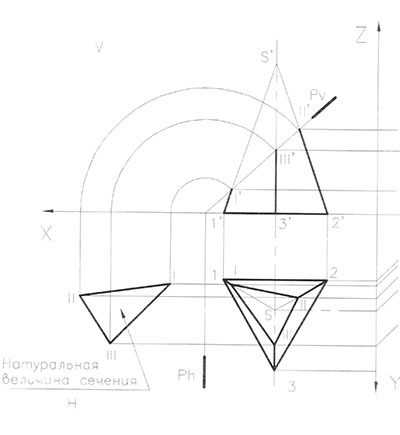
Построение натуральной величины сечения. Построенные выше горизонтальная, фронтальная и профильная проекции сечения пирамиды, имеющие вид треугольников, представляют собой искаженные изображения сечения пирамиды.

Истинная (натуральная) величина сечения получается путем совмещения секущей плоскости Р с горизонтальной плоскостью проекций Н. (Рис.79).

Рис. 79

Построение натуральной величины сечения пирамиды практически не отличается от построения натуральной величины сечения призмы, описанное выше. (Раздел 8.4.1.).

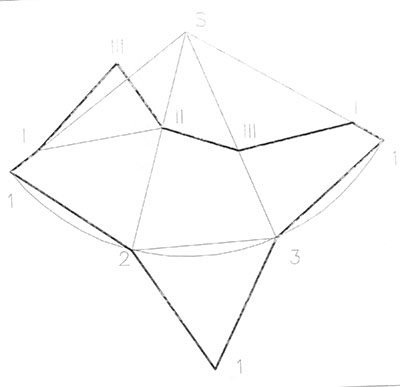
Построение развертки поверхности усеченной пирамиды. Рис. 80. Предварительно построим развертку боковой поверхности не усеченной пирамиды. Задаемся положением т. S на листе и проводим из нее дугу радиусом, равным натуральной величине длины бокового ребра пирамиды. Таким ребром для данной пирамиды является ребро S3 на профильной проекции. Т.к. на горизонтальной проекции это ребро параллельно оси Y, то на профильной проекции оно проецируется в натуральную величину.

Рис. 80

Задаемся положением т. 1 на этой дуге. Последовательно откладываем от нее столько одинаковых отрезков (хорд), сколько боковых граней у пирамиды, в данном случае три. Длина хорды равна стороне основания пирамиды, определенной по горизонтальной проекции. Получаем точки 2, 3 и 1 Соединим их последовательно с т. S. Между точками, например, 2 и 3 пристроим основание пирамиды, взятое с плана. Получена полная развертка поверхности не усеченной пирамиды.

Для построения развертки боковой поверхности усеченной пирамиды необходимо определить натуральную величину всех усеченных ребер. На профильной проекции все точки сечения перенесем на ребро s"3" линиями параллельными основанию пирамиды (т.с и d). Затем каждый отрезок ребра от т. s" до соответствующей точки сечения переносим на соответствующее ребро на развертке. Соединив эти точки на развертке, получим ломаную линию, соответствующую линии сечения боковой поверхности пирамиды.

Затем к линии сечения на развертке (например, между точками I и II) пристраиваем треугольник натуральной величины сечения, полученный на рис.79.

Развертки поверхности геометрических тел представляют собой чертежи - выкройки из бумаги и служат для выполнения макета фигуры.


Практические занятия по теме «Пирамида».

Упражнение 1. Вычертить ортогональные проекции правильной пирамиды с заданными размерами и ее прямоугольную изометрию. Найти точки на поверхности пирамиды.

Упражнение 2. Вычертить ортогональные проекции и аксонометрию усеченной пирамиды с заданными размерами, и ее прямоугольную изометрию. Сечение пирамиды наклонной плоскостью под произвольным углом к основанию.

Упражнение 3. Построить натуральную величину сечения и развертку усеченной пирамиды при произвольном угле наклона секущей плоскости.

Цель задания. Изучить особенности построения правильной пирамиды в ортогональных проекциях и в аксонометрии.

Методические указания. После выполнения простых упражнений могут решаться более сложные задачи по усмотрению преподавателей. При обводке чертежей тушью толщина линий должна соответствовать их назначению. Все линии построения обводить тушью линиями толщиной около 0,1 мм.

8.5. Тела вращения.

8.5.1. Цилиндр.

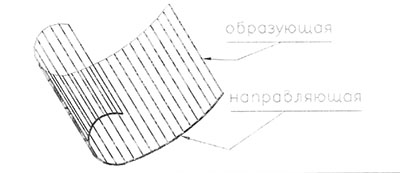
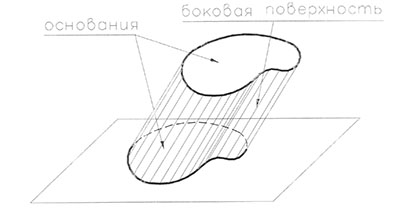
Цилиндрическая поверхность образуется движением прямой линией - образующей, параллельно самой себе и при своем движении пересекающей некоторую кривую, называемую направляюще й. Рис.81. Существует бесчисленное множество цилиндрических поверхностей. Если направляющая - замкнутая, то такая цилиндрическая поверхность называется замкнутой. Рис.82.

Рис. 81

Рис. 82

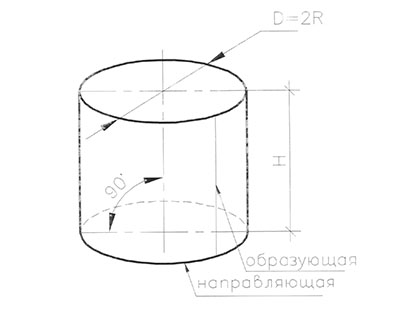
Цилиндр (греч. - kylindros - валик) - тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя секущими ее плоскостями. Цилиндрическая часть поверхности называется боковой поверхностью цилиндра, а плоские части называются основаниями цилиндра. Рис. 82. Цилиндр называется прямым, если плоскости оснований перпендикулярны образующим. Прямой цилиндр называется круговым, если его основание круг и эллиптическим, если его основание эллипс.

Таким образом, прямой круговой цилиндр образуется при движении образующей по окружности параллельно оси вращения, проходящей через центр основания и перпендикулярной ему. В данном учебнике рассматривается только такой, поэтому далее он называется просто цилиндр. Пропорции цилиндра определяются отношением диаметра основания (D=2R) к его высоте (Н). Рис.83.

Рис. 83

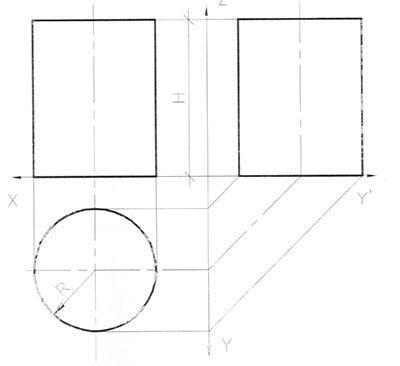
Построение ортогональных проекций цилиндра приведено на рис.84. Горизонтальная проекция цилиндра представляет собой круг, равный основанию цилиндра. Каждая его образующая проецируется в точку, а вся боковая поверхность - в кривую линию (окружность). На фронтальную и профильную проекции цилиндр проецируется в виде прямоугольника, ширина которого равна диаметру основания. А высота равна высоте цилиндра. Вертикальные стороны прямоугольников - проекции крайних (очерковых) образующих цилиндра.

Рис. 84

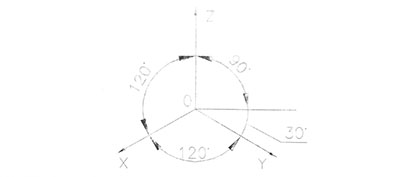
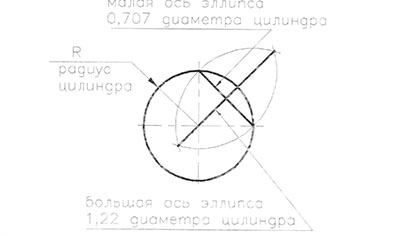
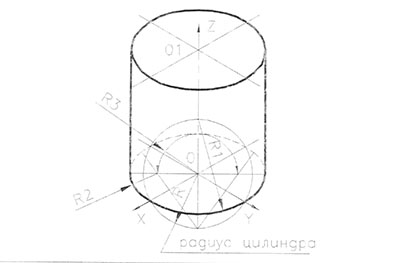
Построение цилиндра в прямоугольной изометрии приведено на рис.85. Построение начинаем с расположения аксонометрических осей OX, OY, OZ, проведя их под углом 120° друг к другу. Рис. 85а. Ось цилиндра направим по оси OZ и отложим на ней высоту цилиндра. Через точку 01 проведем аксонометрические оси 01X1 параллельно ОХ и 01Y1 параллельно 0Y. Принимая точки О и 01 за центры верхнего и нижнего оснований цилиндра, строим два одинаковых овала. (Рис.85в) предварительно найдя большую и малую ось эллипса (Рис.856) основания цилиндра. Затем проводим вертикальные касательные к верхнему и нижнему овалам, которые будут крайними (очерковыми) образующими цилиндра. Рис.85в. Невидимую часть нижнего основания цилиндра выполним штриховой линией.

Рис. 85а

Рис. 85б

Рис. 85в

Построение точек на поверхности цилиндра в ортогональных и аксонометрической проекциях показано на рис.86. Точка А расположена на боковой поверхности цилиндра. По ее фронтальной проекции а' находим ее горизонтальную проекцию (а), лежащую на окружности основания цилиндра. Профильная проекция (а") точки А строится обычным способом нахождения ее координат (ах, ay, az) по осям. На прямоугольной изометрии цилиндра точка А также строится обычным способом по ее координатам (ах, ay, az).

Рис. 86

Построение развертки поверхности цилиндра показано на рис.87. Разверткой поверхности называют плоскую фигуру, образуемую последовательным совмещением плоских элементов этой поверхности с одной плоскостью.

Рис. 87а

Размеры всех элементов развертки имеют натуральную величину.

Полная поверхность цилиндра состоит из боковой цилиндрической поверхности и двух равных оснований (верхнего и нижнего). Если перекатывать цилиндр по плоскости, то его боковая поверхность развернется в прямоугольник, высота которого равна высоте цилиндра, а ширина равна длине окружности основания цилиндра (2tiR=jiD). На этом основании и строится прямоугольник указанных размеров с пристроенными к нему двумя кругами, равными основанию цилиндра. Рис.87а.

Если не требуется точной развертки цилиндра, то можно построить его приближенную развертку графическим способом. Для этого делят периметр основания цилиндра на 12 (16 или 20) равных частей, измеряют по хорде длину 1/12 части окружности основания и откладывают ее 12 раз на длине прямоугольника вместо величины 2лR, определяемой вычислениями.

Для перенесения на развертку точки К, принадлежащей боковой поверхности цилиндра, через точку К проводят образующую цилиндра. Она пересекает основание в точке С. Отложив расстояние 1-С на развертке цилиндра, строим соответствующую образующую и на заданной высоте h находим точку К. Рис. 876.

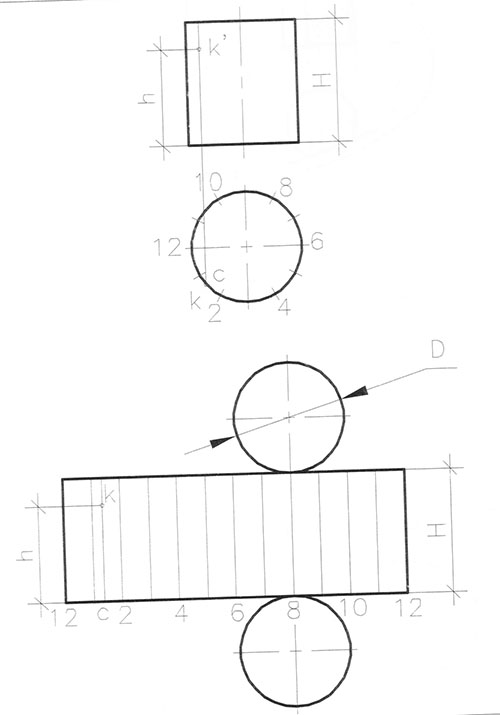
Рис. 87б

При построении усеченного цилиндр а линия плоского наклонного сечения поверхности цилиндра на развертке будет иметь вид синусоиды (лекальная кривая). Ее построение показано на рис.88.

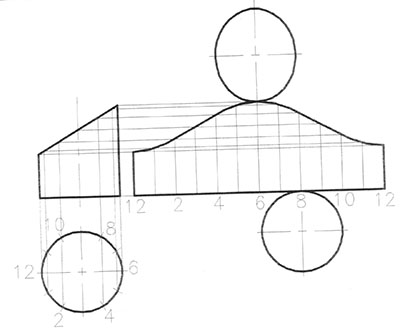
Рис. 88

Построение различных видов сечения цилиндра проецирующей плоскостью Р показаны на рис.89.

При пересечении цилиндра горизонтальной проецирующей плоскостью образуется так называемое нормальное сечение поверхности, натуральная величина которого равна его основанию. Рис.89а.

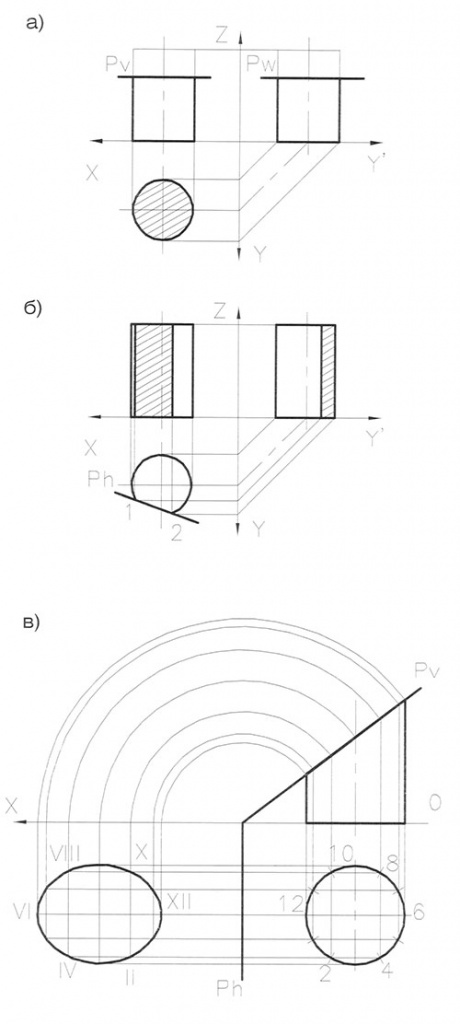
Рис. 89

При пересечении цилиндра вертикальной проецирующей плоскостью (секущая плоскость Р проходит по образующим цилиндра) на фронтальной и профильной проекциях образуется сечение в виде прямоугольника, высота которого равна высоте цилиндра, а ширина определяется положением секущей плоскости. Рис.896.

Построение сечения цилиндра наклонной секущей плоскостью Р перпендикулярной фронтальной плоскости проекции показано на рис.89в. В данном случае сечение получается в виде эллипса, фронтальная проекция которого совпадает со следом секущей плоскости Pv, а горизонтальная -с горизонтальной проекцией цилиндра. Натуральная величина эллипса сечения (I - XII) получена методом совмещения секущей плоскости с плоскостью Н. Указанные точки эллипса находят путем пересечения образующих с заданной плоскостью.

При сечении цилиндра наклонными плоскостями выявлено три случая:

- угол наклона секущей плоскости меньше 45° -на профильной проекции получаем эллипс, вытянутый горизонтально; при угле наклона больше 45° -эллипс вытянут вертикально; а при угле наклона секущей плоскости равным 45° - эллипс проецируется в окружность. Рис.90.

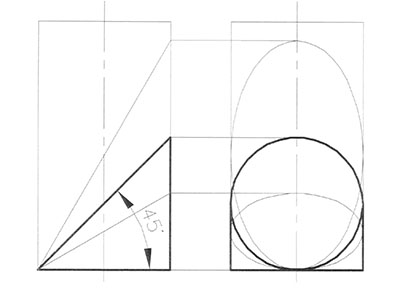
Рис. 90

Практические занятия по теме «Цилиндр».

Упражнение 1. Вычертить ортогональные проекции прямого кругового цилиндра с заданным радиусом основания и высотой.

Упражнение 2. Вычертить аксонометрическое изображение прямого кругового цилиндра в прямоугольной изометрии, предварительно построив большую и малую ось эллипса основания.

Упражнение 3. Построить проекции точек на видимой и невидимой частях поверхности цилиндра на ортогональном и аксонометрическом изображении цилиндра.

Упражнение 4. Построить развертки целого и усеченного цилиндра под углами 30°, 45° и 60°.

Цель задания. Изучить особенности построения прямого кругового цилиндра в ортогональных проекциях и в аксонометрии.

Методические указания. После выполнения простых упражнений могут решаться более сложные задачи по усмотрению преподавателей.

Дата добавления: 2014-11-06