Построение точек на поверхности тора

Построение проекций тора

Круговое кольцо (или открытый тор) имеет горизонтальную проекцию в виде двух концентрических окружностей, разность радиусов которых равна толщине кольца или диаметру образующей окружности (рисунок 145). Фронтальная проекция ограничивается справа и слева дугами полуокружностей диаметра образующей окружности.

На рисунке 144, а и б приведены два вида закрытого тора. В первом случае образующая дуга окружности радиуса R отстоит от оси вращения на расстоянии меньше радиуса R, а во втором случае — больше. В обоих случаях фронтальные проекции тора представляют собой действительный вид двух образующих дуг окружности радиуса R, расположенных симметрично по отношению к фронтальной проекции оси вращения. Профильными проекциями тора будут окружности.

а б

Рисунок 144

В случае, когда точка А лежит на поверхности кругового кольца и дана одна ее проекция, для нахождения второй проекции этой точки применяется вспомогательная окружность, проходящая через данную точку А и расположенная на поверхности кольца в плоскости, перпендикулярной оси кольца (рисунок 145).

Если задана фронтальная проекция A'' точки А, лежащей на поверхности кольца, то для нахождения ее второй проекции (в данном случае — горизонтальной) через A" проводят фронтальную проекцию вспомогательной окружности — отрезок горизонтальной прямой линии 2''2''. Затем строят горизонтальную проекцию 2'2' этой окружности и на ней, применяя линию связи, находят точку A'.

Если задана горизонтальная проекция B' точки B, расположенной на поверхности этого кольца, то для нахождения фронтальной проекции этой точки через 1' проводят горизонтальную проекцию вспомогательной окружности радиуса R₁. Затем через левую и правую точки 1' и 1' этой окружности проводят вертикальные линии связи до пересечения с фронтальными проекциями очерковой образующей окружности радиуса R и получают точки 1'' и 1''. Эти точки соединяют горизонтальной прямой, которая представляет собой фронтальную проекцию вспомогательной окружности (она будет видима). Проводя вертикальную линию связи из точки B' до пересечения с прямой 1''1'' получаем искомую точку B''.

Такие же приемы построения применимы и для точек, находящихся на поверхности тора.

Рисунок 145

Построение аксонометрического изображения тора можно разделит на три этапа (рисунок 146). Сначала строится в виде эллипса проекция радиальной осевой линии (траектория движения центра образующей окружности). Затем определяем радиус сферы, касающейся тора по образующей (окружности). Для этого строим в виде меньшего эллипса проекцию фронтальной очерковой образующей тора. Радиус сферы определим как длину отрезка О₁F от центра эллипса до точки на этом эллипсе, лежащей на большой оси эллипса (перпендикулярной Oy). Далее строим большое количество окружностей радиусом R_сферы с центрами на проекции радиальной осевой тора О_{1 …} О_n (чем больше, тем точнее контур будущего тора). В завершение проводим линию контура тора как линию, касающуюся каждой окружности сферы.

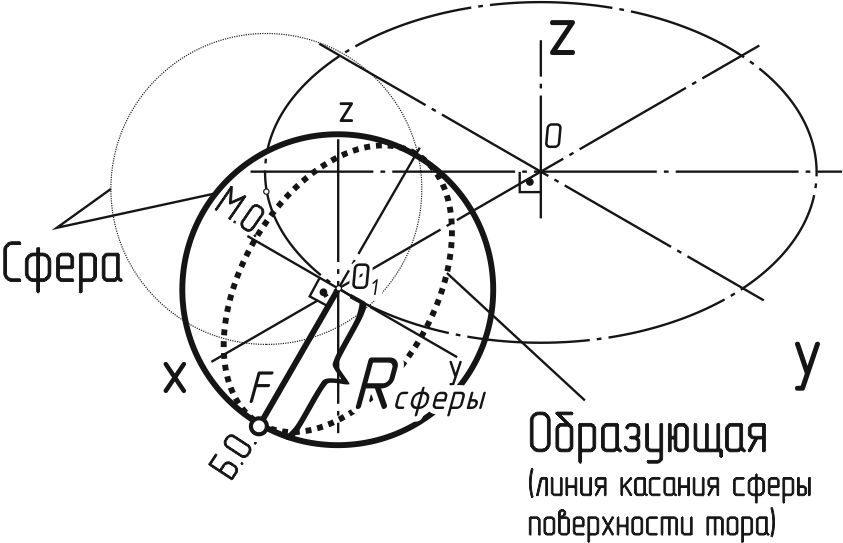
а б

Рисунок 146

В аксонометрической проекции точку А, находящуюся на поверхности тора, строят по трем координатам: X_А, Y_А и Z_А. Эти координаты последовательно откладывают по направлениям, параллельным изометрическим осям.

Дата добавления: 2014-11-06