Динамика вращательного движения твердого тела. Момент силы. Момент импульса

Вектор линейной скорости любой точки А твердого тела, вращающегося вокруг некоторой оси с угловой скоростью, равен векторному произведению на радиус-вектор заданной точки А относительно произвольной точки О на оси вращения.

Модуль вектора линейной скорости

,

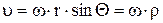где 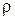– радиус окружности, по которой движется точка А.

Вектор полного ускорения точки А

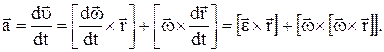Одно из слагаемых в данном выражении является танген-циальным ускорением точки А – 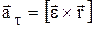, модуль тангенциального ускорения , другое – нормаль-ным ускорением точки А . Модуль нормального ускорения .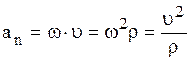

Вектор полного ускорения и его модуль равен

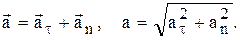
При описании динамики вращательного движения твердого тела используют момент силы 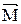и момент импульса .

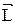Моментом силы относительно точки О называют вектор 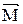, равный векторному произведению радиуса-вектора 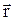точки приложения силы и вектора силы

.

А

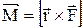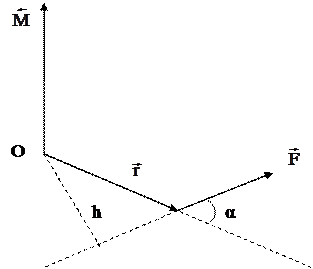Вектор мо-мента силы перпендикулярен плоскости, в которой лежат вектора 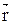и 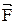, и связан с направ-лением вектора силы правилом правого винта (рис. 3): если вра-щать от 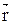к 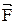по кратчайшему пу-ти, то поступа-тельное направле-ние винта совпадает с направлением 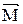. Угол 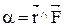, а плечо вектора относительно точки О .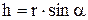

Модуль вектора момента силы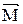

.

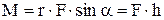Размерность момента силы в СИ .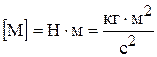

Момент импульса 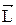во вращательном движении выполняет ту же роль, что и импульс в поступательном движении.

Пусть положение частицы А относительно некоторой точки О, выбранной системы отсчета задано радиус-вектором 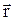, а 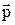есть её импульс в этой системе отсчета (рис.4).

Моментом им-пульса частицы А относительно точки О называется вектор 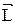, равный векторному произведению векторов 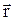и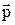

.

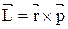Модуль вектора момента импульса 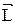– 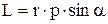, где угол 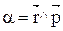(рис. 4). Вектор 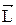перпендикулярен плоскости, в которой лежат вектора 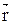и 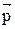, и связан с направлением вектора импульса частицы правилом правого винта (рис. 4): если вращать от 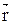к 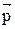по кратчайшему пути, то поступательное направление винта совпадает с направлением 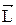. Плечо вектора 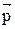относительно точки О есть .

Размерность момента импульса измеряется в СИ .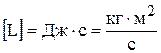

Момент импульса обладает свойством аддитивности: момент импульса механической системы материальных точек относительно неподвижной точки О 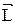равен сумме моментов импульсов всех материальных точек системы 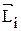относительно точки О.

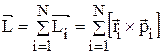
Для установления связи между моментом силы 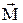и моментом импульса 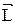продифференцируем полученное уравнение по времени.

,

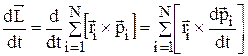учитывая, что

.

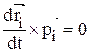Для i-той материальной точки системы второй закон Ньютона, основной закон динамики, имеет вид

,

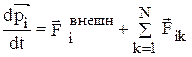где 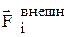– результирующая всех внешних сил, действующих на i-тую материальную точку системы, 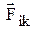– внутренняя сила, действующая на i-тую материальную точку системы со стороны k-той точки.

.

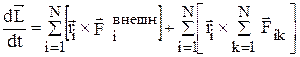По третьему закону Ньютона сумма внутренних сил равна нулю и, следовательно,

.

Обозначим .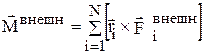

С учетом этого изменение момента импульса со временем будет

.

Полученное соотношение называется основным уравнением динамики вращательного движения системы частиц: Первая производная по времени от момента импульса механической системы частиц относительно неподвижной точки равна сумме всех моментов внешних сил, действующих на систему.

Рассмотрим вращательное движение системы частиц относительно неподвижной оси, с которой мы, например, совместим ось 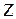. Моментом силы относительно оси Z называется проекция на эту ось вектора момента силы 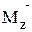относительно любой точки, выбранной на данной оси.

Моментом импульса механической системы относительно оси Z называется проекция на эту ось вектора момента импульса системы относительно любой точки выбранной на рассматриваемой оси.

Из основного уравнения динамики вращательного движения следует, что первая производная по времени от момента импульса механической системы частиц (тела) относительно неподвижной оси равна сумме всех моментов внешних сил относительно этой оси действующих на систему.

Для декартовой системы координат

, , .

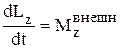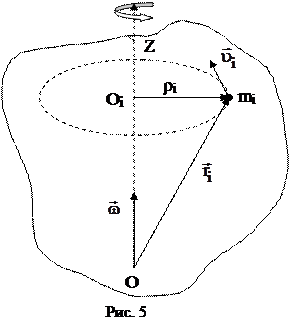Рассмотрим уравнение динамики твердого тела, вращающегося вокруг неподвижной оси. Пусть тело совершает вращательное движение относительно неподвижной оси Z, совпадающей с осью OZ прямоугольной системы координат (рис.5). Для получения уравнения динамики вращательного движения твердого тела вращающегося относительно неподвижной оси, вычислим проекцию момента импульса для тела на ось Z, вращающегося с постоянной угловой скоростью 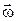. Радиус-вектор материальной точки 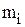, входящей в состав тела, равен 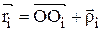, где O_i – центр окружности радиуса, по которой движется материальная точка .

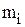Момент импульса тела 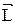относительно начала координат О равен сумме моментов импульса всех материальных точек тела массой 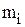относительно О:

,

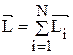где .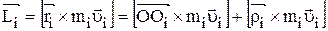

Вектор, равный 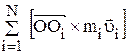, перпендикулярен оси ОZ, а вектор направлен вдоль оси OZ. Проекция вектора момента импульса относительно начала координат О на ось OZ .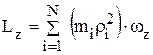

Величина 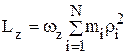, где есть момент инерции тела относительно оси Z.

Дата добавления: 2014-11-06