Электричество

Сводка основных формул

Электрическое поле в вакууме

В природе существует два вида зарядов: положительные и отрицательные.

По закону Кулона точечные заряды q ₁ и q ₂, взаимодействуют с силой

,

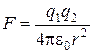где 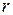- расстояние между зарядами, e₀ = 8,85×10^-12 Ф/м – электрическая постоянная. Сила направлена вдоль прямой, соединяющей заряды. Одноименные заряды отталкиваются, а разноименные – притягиваются.

Напряженность электрического поля 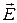равна отношению силы, действующей на заряд, к величине заряда

.

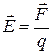Напряженность поля точечного заряда определяется выражением

.

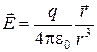По принципу суперпозиции напряженности полей складываются

.

По теореме Остроградского – Гаусса поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на e₀

.

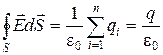Напряженность поля бесконечной равномерно заряженной плоскости с поверхностной плотностью s равна

.

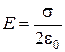Потенциал поля точечного заряда равен

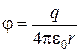
Для потенциала поля системы зарядов справедлив принцип суперпозиции

.

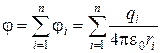Проекция вектора напряженности 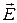на произвольную прямую х в пространстве связана с потенциалом выражением

.

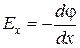Работа сил электрического поля по перемещению заряда q из точки с потенциалом j₁в точку с потенциалом j₂ равна

.

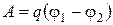Электрическое поле в веществе

Электрическое поле в диэлектриках характеризуют электрическим смещением 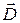, которое определяется соотношением

,

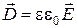где e - относительная диэлектрическая проницаемость вещества.

Теорема Остроградского-Гаусса для вектора 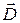имеет вид

.

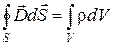где - объемная плотность заряда.

Для однородного и изотропного диэлектрика сила Кулона, напряженность и потенциал поля точечного заряда в e раз меньше чем в вакууме

, .

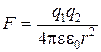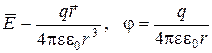Проводники имеют свойство накапливать заряд. Емкость C уединенного проводника определяется отношением его заряда q к потенциалу j

.

Емкость конденсатора равна отношению его заряда q к напряжению U между обкладками

.

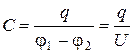Емкость плоского конденсатора равна

,

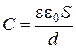где S – площадь пластин конденсатора, d - расстояние между пластинами.

Заряженный конденсатор имеет энергию

.

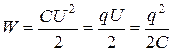Конденсаторы соединяют в батареи последовательно и параллельно. При последовательном соединении заряд конденсаторов одинаковый, напряжения складываются, емкость батареи определяется выражением

, , .

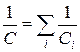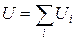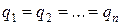При параллельном соединении емкость батареи и заряды складываются, а напряжение на конденсаторах одинаковое

, , .

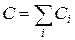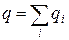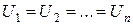Электрическое поле обладает энергией. Плотность энергии w электрического поля (энергия единицы объема) определяется выражением

.

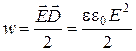Постоянный ток

Сила тока равна отношению заряда dq, перенесенного через поперечное сечение проводника, ко времени dt, за которое перенесен заряд

.

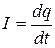Плотность тока 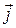определяется величиной заряда носителей тока, их концентрацией 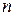и средней скоростью упорядоченного движения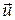

.

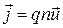Сила тока выражается через плотность тока интегрированием по поперечному сечению проводника

.

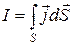По закону Ома сила тока I на участке цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R

.

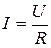Сопротивление цилиндрического проводника длиной l с площадью поперечного сечения S рассчитывается по формуле

,

где 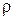- удельное сопротивление материала проводника.

В дифференциальной форме закона Ома плотность тока 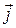пропорциональна напряженности электрического поля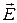

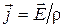
Количество теплоты 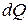, выделяющееся в проводнике с сопротивлением R при прохождении по нему тока I за малое время dt, по закону Джоуля-Ленца, равно

.

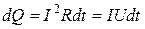Для замкнутой цепи по закону Ома сила тока пропорциональна ЭДС и обратно пропорциональна полному сопротивлению

,

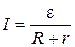где - ЭДС источника тока, R и r – внешнее и внутреннее сопротивление цепи.

При последовательном соединении проводников сила тока в проводниках одинакова, а напряжения и сопротивления складываются

, , .

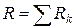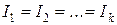При параллельном соединении проводников напряжение на проводниках одинаковое, а сила тока и величины, обратные сопротивлению, складываются

, , .

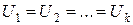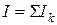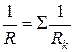Для расчета разветвленных цепей используются два правила Кирхгофа.

Первое правило: алгебраическая сумма токов в узле равна нулю

.

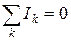Втекающие в узел токи - положительные, а вытекающие - отрицательные.

Второе правило: для любого замкнутого контура алгебраическая сумма произведений в ветвях равна алгебраической сумме ЭДС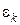

.

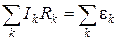Положительными считаются токи и ЭДС, направление которых совпадает с направлением обхода контура.

Магнитное поле

По закону Био–Савара–Лапласа элемент тока 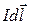создает магнитное поле с индукцией

.

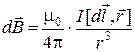Здесь 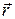- радиус вектор, проведенный от элемента тока до точки наблюдения, m ₀ = 4p×10^-7 Гн/м – магнитная постоянная.

Для магнитного поля справедлив принцип суперпозиции

,

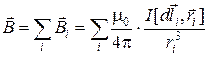где 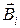- индукция магнитного поля отдельного проводника.

Индукция магнитного поля бесконечного прямого проводника равна

,

где r – расстояние до проводника. Линии индукции - концентрические окружности, их направление согласовано с током правилом правого винта.

Индукция магнитного поля в центре кругового тока радиуса R равна

.

Циркуляция вектора магнитной индукции по любому замкнутому контуру L пропорциональна алгебраической сумме токов, охваченных контуром

.

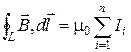Ток считается положительным, если его направление согласовано с обходом контура по правилу правого винта.

На элемент тока 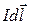в магнитном поле с индукцией 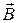действует сила Ампера

.

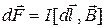Направление силы определяется по правилу правого винта.

На контур с током в магнитном поле действует момент сил, равный

,

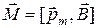где 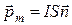- магнитный момента контура, S – его площадь, 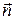- нормаль.

Магнитным потоком через поверхность S называется интеграл по поверхности

,

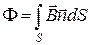где 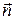- нормаль к поверхности.

Электромагнитная индукция

При изменении магнитного потока, пронизывающего замкнутый контур, в нем возникает индукционный ток (явление электромагнитной индукции). По закону Фарадея ЭДС индукции в контуре равна скорости изменения магнитного потока

.

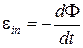Знак «минус» соответствует правилу Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей.

Самоиндукция – возникновение ЭДС индукции при изменении тока в контуре. По закону Фарадея ЭДС самоиндукции определяется выражением

,

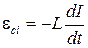где L – индуктивность (коэффициент самоиндукции) контура.

Магнитное поле длинного соленоида однородное, сосредоточено внутри соленоида, индукция магнитного поля направлена вдоль оси соленоида и равна

,

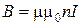где m - относительная магнитная проницаемость вещества внутри соленоида, 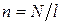- количество витков на единицу длины соленоида, N и l –количество витков и длина соленоида.

Индуктивность и энергия длинного соленоида, объем которого V, равны

, .

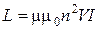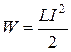Переменный ток

Переменным называется ток, изменяющийся со временем по гармоническому закону

.

В цепи из последовательно соединённых конденсатора, катушки индуктивности и резистора сила тока изменяется по закону

,

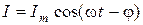а амплитудные значения силы тока и напряжения связаны законом Ома

,

, , .

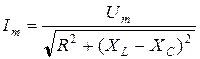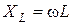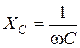Здесь X_L и X_C – индуктивное и ёмкостное сопротивления, j - сдвиг фаз между током и напряжением, 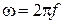- циклическая частота, f – частота.

Средняя мощность в цепи переменного тока зависит от сдвига фаз j и определяется законом Джоуля – Ленца

,

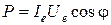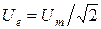где и - действующие значения

Примеры решения типовых задач

1. В центр квадрата, в вершинах которого находятся заряды q = 2,33 нКл, помещен отрицательный заряд 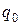. Найти величину этого заряда, если результирующая сила, действующая на каждый заряд, равна нулю.

Решение. На рис. 1.1 приведено расположение зарядов и силы, действующие на заряд 1 со стороны остальных зарядов. По условию эти силы скомпенсированы

.

Спроектируем это равенство на прямую, совпадающую с диагональю квадрата

.

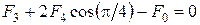Обозначив сторону квадрата 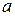и используя закон Кулона, преобразуем это уравнение к виду

.

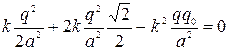Отсюда найдем искомый заряд

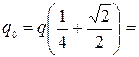2,23 нКл.

2. Два шарика одинакового радиуса и массы 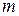= 10 г подвешены на нитях так, что их поверхности соприкасаются, и погружены в керосин. После сообщения шарикам заряда 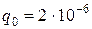Кл они оттолкнулись друг от друга и разошлись на угол 2a = 45°. Найти плотность материала шариков, если расстояние от точки, подвеса до центра шарика l = 20 см. Плотность и относительная диэлектрическая проницаемость керосина 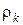= 800 кг/м³, e = 2.

Решение. На каждый из шариков действуют силы: тяжести , натяжения нити 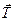, Кулона 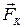и Архимеда (рис. 1.2). Под действием этих сил шарик находится в равновесии, условие которого имеет вид

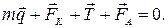
Спроектировав эти силы на ос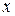и и 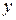, получим следующие уравнения:

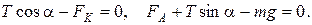(1)

По закону Кулона и Архимеда имеем:

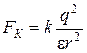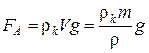, , (2)

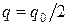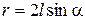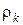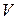где - заряд каждого шарика, который распределился между шариками поровну, - расстояние между шариками, и - плотность и относительная диэлектрическая проницаемость керосина, и - плотность, масса и объем шарика.

Плотность шарика найдем из второго уравнения (2)

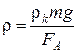. (3)

Из уравнений (1) и (2) найдем силу Архимеда

.

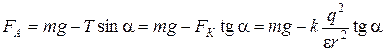После подстановки в (3), получим выражение для плотности

= 4200 кг/м³.

3. Электрон с некоторой начальной скоростью v ₀ влетает в плоский конденсатор параллельно пластинам на равном расстоянии от них. К пластинам конденсатора приложена разность потенциалов U = 300 В. Расстояние между пластинами d = 2 см, длина конденсатора l =10 см. Какова должна быть предельная начальная скорость v ₀ электрона, чтобы электрон не вылетел из конденсатора?

Решение. На электрон при движении между пластинами конденсатора действует электрическая сила 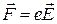, направленная перпендикулярно пластинам, где 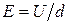- напряженность электрического поля (рис. 1.3). Двигаясь в этом направлении с ускорением 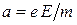, электрон достигнет пластины за время 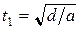. За это время он пролетит вдоль пластин расстояние 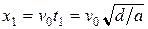. Траекторией электрона будет парабола. Если 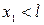, то электрон не вылетит из конденсатора. Из этого неравенства находим ограничение для скорости

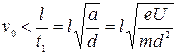
4. Элемент с ЭДС = 1,1 В и внутренним сопротивлением r = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Найти силу тока в цепи, напряжение 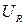во внешней цепи и напряжение 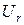внутри элемента. С каким КПД h работает элемент?

Решение. Из закона Ома для замкнутой цепи найдем силу тока

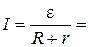0,11 А. (1)

Напряжение 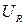на внешней цепи и 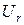внутри элемента найдем из закона Ома для участка цепи

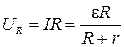= 0,99 В, 0,11 В. (2)

КПД источника тока найдем по отношению полезной мощности 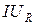к затраченной :

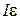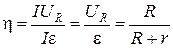= 0,9.

Здесь 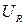и определены из формулы (1) и (2).

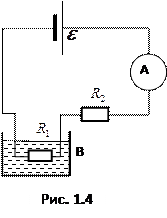
5. В схеме на рис. 1.4 батарея с ЭДС ε = 120 В,
R 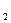= 10 Ом, В — электрический чайник. Амперметр показывает I = 2 А. Через сколько времени закипит V = 0,5 л воды, находящейся в чайнике при начальной температуре
t ₀ = 4° С? Сопротивлением батареи и амперметра пренебречь. КПД чайника h = 76 %.

Решение. Мощность нагревателя определим по закону Джоуля-Ленца

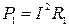. (1)

Сопротивление нагревателя определим из закона Ома для замкнутой цепи

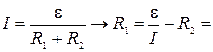50 Ом.

Время нагревания воды найдем из уравнения теплового баланса, которое с учетом КПД нагревателя имеет вид

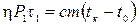, (2)

где 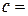4200 Дж/кг×м³ - теплоемкость воды, 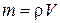- масса воды, 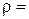1000 кг/м³ - плотность, 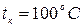- температура кипения. Из уравнения (2) с учетом (1) получим

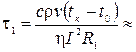22 мин.

6. Найти распределение индукции магнитного поля вдоль оси кругового витка диаметром D = 10 см, по которому течет ток силой I = 10 А. Построить примерный график этой зависимости с нанесением масштаба.

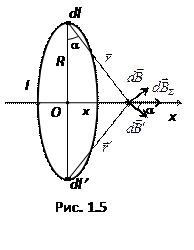
Решение. Для расчета воспользуемся законом Био-Савара-Лапласа и принципом суперпозиции. Выделим на витке два симметрично расположенных элемента 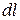и (рис. 1.5.). По закону Био-Савара-Лапласа

,

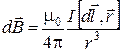эти элементы создают поля с индукцие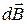й и 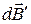, которые в силу симметрии направлены под одинаковыми углами к оси х. Поэтому их сумма будет направлена вдоль этой оси. Отсюда следует, что круговой виток в силу симметрии создает магнитное поле, индукция которого направлена вдоль оси х. Этот факт существенно упрощает решение задачи.

Проекцию 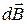на ось х найдем по формуле 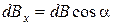. Учитывая, что 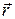^ 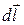, , 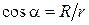получим выражение для проекции

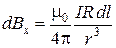. (1)

Индукцию В найдем, проинтегрировав (1) по длине контура

.

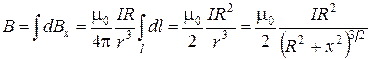Здесь при преобразованиях учтено, что .

График этой зависимости приведен на рис. 1.6.

7. В магнитном поле, индукция которого равна В = 0,05 Тл, вращается стержень длиною l = 1 м (рис. 1.7). Ось вращения, проходящая через один из концов стержня, параллельна силовым линиям магнитного поля. Найти магнитный поток F, пересекаемый стержнем при каждом обороте.

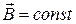Решение. Магнитный поток определяется выражением . По условию задачи и 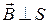. За один оборот стержень очерчивает круг площадью , как показано на рис. 1.7. Тогда для потока получим

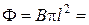0,15 Вб.

8. Электрон, ускоренный разностью потенциалов U = 1000 В, влетает в однородное магнитное поле, перпендикулярное направлению его движения. Индукция магнитного поля B = 1,19×10 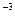Тл. Найти радиус R кривизны траектории электрона, период T обращения его по окружности, момент импульса L электрона.

Решение. При ускорении электрона электрическое поле совершает работу , которая идет на сообщение ему кинетической энергии 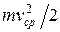. Приравнивая выражения, найдем скорость электрона .

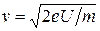В магнитном поле на электрон действует сила Лоренца 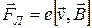. По II закону Ньютона движение электрона описывается уравнением

.

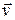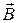Сила Лоренца перпендикулярна и . По условию и магнитное поле однородное. Поэтому электрон будет двигаться по окружности с ускорением 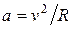. Такое движение описывается уравнением

.

Отсюда найдем радиуса орбиты электрона

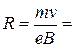9 см.

Момент импульса электрона найдем по формуле 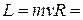1,5·10^-24кг·м^-2/с.

Период обращения электрона найдем, наделив длину окружности (путь) на скорость: 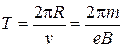= 30 нс. Отсюда видно, что период обращения электрона не зависит от его скорости.

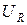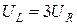9. В цепь переменного тока напряжением U = 220 В включены последовательно емкость С, резистор R и индуктивность L. Найти напряжение на резисторе, если известно, что напряжения на конденсаторе , а на индуктивности . Определить сдвиг фаз j между током и напряжением и мощность Р в цепи для R = 100 Ом.

Решение. По закону Ома для переменного тока имеем

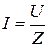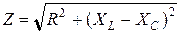, , (1)

где 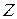- полное сопротивление, 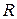, 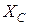и 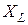активное, емкостное и индуктивное сопротивления отдельных элементов цепи.

При последовательном соединении через все элементы цепи протекает одинаковый ток. Напряжения на отдельных элементах найдем согласно закону Ома найдем по формулам

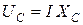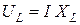, , . (2)

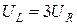Отсюда с учетом условия задачи и определим сопротивления конденсатора, катушки и полное сопротивление цепи

, , .

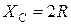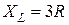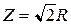Из уравнений (1) и (2) найдем силу тока в цепи и напряжение на резисторе

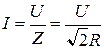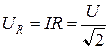, = 156 В.

Сдвиг фаз между током и напряжением найдем по формуле

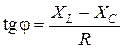= 1, j = 45°.

Мощность определим по закону Джоуля-Ленца для переменного тока

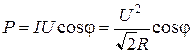= 242 Вт.

Задания для аудиторной и самостоятельной работы по теме Электричество должны быть выполнены и представлены на кафедру Общей физики и дидактики физики не позднее 14 ноября 2014г. Решение задач приводится в развернутом виде.

Занятие №1. Электростатика в вакууме. Закон Кулона

Дата добавления: 2014-11-06