Второе начало термодинамики понятие энтропии

Тепловая энергия, образующаяся в организме, представляет собой конкретную форму связанной энергии биологической си­стемы, так как в условиях жизнедеятельности она не может быть преобразована ни в одну из форм работ, совершаемых ор­ганизмом. Чем же определяется связанная энергия?

Вспомним, что W_связ зависит от степени неупорядоченности молекулярного движения, а ее количественной мерой служит температура. Поэтому W_связ пропорциональна Т. Однако вели­чина связанной энергии в разных системах, имеющих одинако­вую температуру, не всегда одинакова. Следовательно, степень неупорядоченности молекулярного движения зависит не только от температуры, но и от еще каких-то свойств системы. Эти свойства Клаузиус (1865) выразил в виде коэффициента, кото­рый однозначно связывает значения W_связ и Т. Коэффициент принято обозначать буквой s и называть энтропией. С вводом энтропии зависимость связанной энергии системы от ее темпе­ратуры выглядит так:

W_связ= sT (1)

откуда

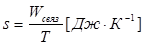(2)

Энтропия — это физическая величина, характеризующая значе­ние связанной энергии данной системы, приходящееся на еди­ницу температуры (1 К).

Так как W_связ =sT, то выражение для внутренней энергии системы приобретает такой вид:

U=G+sT '(3)

откуда

G = U-sT. (4)

Более строгое рассмотрение показывает, что эта формула справедлива только при постоянной температуре и постоянном объеме. В других условиях, например, при постоянной темпера­туре, но изменяющемся объеме, выражение для свободной энер­гии имеет более сложный вид:

G = U — sT + pV. (5)

Для изобарических процессов при постоянной температуре можно пользоваться формулой (4). В этом случае свободную энергию обычно обозначают буквой F и называют свободной энергией по Гельмгольцу, тогда как величину G, определяемую по формуле (5), принято называть свободной энергией по Гиббсу.

В^; организме человека температура постоянна, а изменения объема, как правило, невелики. Поэтому при рассмотрении большинства жизненных процессов можно пользоваться поня­тием свободной энергии по Гельмгольцу (F). В биохимии за­частую рассматривают процессы, связанные с выделением или поглощением газов (кислород, углекислый газ и др.); так как объем газа при этом меняется, применяют понятие свободной энергии по Гиббсу (G).

Практический интерес представляет не сама по себе свобод­ная энергия, а ее изменение. При V—const и T = const

ΔF=ΔU-TΔs (6)

Если объем изменяется, то изменение свободной энергии опре­деляется по формуле

ΔG=ΔU-TΔs+pΔV (7)

Говоря о запасе энергии в какой-либо системе, интересуют­ся прежде всего тем, какую работу она может совершить. Ясно, что при этом следует учитывать не полную, а только свободную энергию. Пищевые продукты важны для человека потому, что он получает при их усвоении свободную энергию для соверше­ния работы. В ванне горячей воды содержится больший запас энергии, чем в килограмме хлеба, но за счет ее организм, по­груженный в ванну, не способен совершить работу, так как почти вся эта энергия является связанной.

Таким образом, энергия в различных формах имеет разную практическую ценность, которая тем выше, чем большую часть этой энергии можно преобразовать в работу, то есть чем меньше доля связанной энергии, мерой которой служит энтропия. Следовательно, чем ниже энтропия системы, тем выше ценность свойственной ей внутренней энергии.

Выше говорилось, что превращение свободной энергии в связанную называют диссипацией (рассеянием) энергии. Не­трудно понять, что таким превращением сопровождается лю­бое преобразование более ценной формы энергии в менее цен­ную. Например, преобразование химической энергии, заклю­ченной в биологических макромолекулах, в тепловую есть дис­сипация энергии.

Энтропия является функцией состояния системы. Это озна­чает, что величина энтропии целиком определяется параметра­ми системы в данный момент и совершенно не зависит от ее «истории», то есть от того, как система пришла в данное со­стояние. Функцией состояния являются и некоторые другие фи­зические величины, например, потенциальная энергия: ее зна­чение зависит только от высоты, на которую поднято тело, но не от того, каким путем оно достигло этой высоты. А вот коли­чество тепла не является функцией состояния системы: зная, например, что литр воды находится при температуре 303 К, мы ничего не можем сказать о том, какое количество тепла по­лучила или отдала вода. Чтобы ответить на этот вопрос, нужно знать, во-первых, исходное состояние и, во-вторых, как именно протекал процесс изменения температуры, в частности, совер­шалась при этом работа или нет.

Рассмотрим теперь как практически можно вычислить зна­чение энтропии. Согласно положениям термодинамики, изме­нение энтропии при элементарном обратимом процессе опреде­ляется выражением

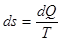(8)

или, при обратимом переходе из некоторого состояния (1) в со­стояние (2):

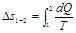
Может показаться, будто эти формулы не имеют практиче­ского значения, поскольку все реальные процессы необратимы. Однако ими успешно пользуются и практических расчетах. Де­ло в том, что Δs₁-₂ всегда одно и то же, независимо от процесса, посредством которого осуществлен переход системы (1) в состояние (2), так как энтропия — функция состояния. Поэтому расчеты, проведенные применительно к обратимому процессу, оказываются правильными и для необратимого про­цесса, но их гораздо проще выполнять.

Найдем, например, изменение энтропии при нагревании воды от 293 К до 373 К Это необратимый процесс, Так как в хо­де его неизбежны потери энергии за счет утечки тепла в окру­жающую среду, создания конвекционных потоков и т. д. Одна­ко при вычислении энтропии этим можно пренебречь и исполь­зовать формулы, отображающие изменения энтропии при обра­тимом процессе:

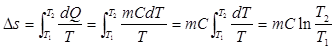
где С — удельная теплоемкость воды. Подставляя числа, полу­чаем:

Δs=1 кг 4180 Дж кг^-1 К^-1 ln (373/293)≈1220 Дж К^-1 (10)

Так как энтропия — функция состояния, то изменение энтро­пии будет таким же и в реальном необратимом процессе, хотя затраченное количество тепла будет фактически больше, чем при обратимом процессе.

Зная изменение энтропии, легко подсчитать изменение сво­бодной энергии системы как по Гельмгольцу, так и по Гиббсу (формулы 4, 5).

При выяснении понятия энтропии учащиеся нередко задают вопрос: есть ли смысл вводить это понятие, если энтропия вы­ражается через Q и Т, не проще ли прямо выражать свобод­ную энергию через количество тепла? Такой вопрос возникает лишь в том случае, если не учитывать, что количество тепла, которое система получила или отдала, сильно зависит от спо­соба перехода ее из одного состояния в другое, тогда как эн­тропия как функция состояния не зависит от этого. Поэтому на практике проще вычислить изменение энтропии. Такой расчет позволяет отвлечься от протекания процесса и учитывать толь­ко начальное и конечное состояние системы.

Кроме того, понятие энтропии имеет огромное теоретическое значение. Энтропия является физической величиной, количест­венно характеризующей те особенности молекулярного строе­ния системы, от которых зависят энергетические преобразования в ней, в частности их направление (греческое слово εντρωπα переводится на русский язык как превращение, развитие, эво­люция, поворот). Эту связь энтропии с молекулярной структу­рой системы понял Л. Больцман, установивший ее статистичес­кий смысл.

Дата добавления: 2014-11-06