Прямая и обратная геодезическая задачи

Зависимость между горизонтальными и дирекционными углами теодолитного хода. Уравнивание (увязка) горизонтальных углов

Зависимость между азимутами истинным, магнитным и дирекционным углом

Вследствие непараллельности между собой меридианов истинный азимут протяженной прямой АВ (рис.9) принимает различные значения в точках А и В. В средних широтах истинный азимут изменяется на одну минуту через каждые один-два километра расстояния по параллели. Это осложняет применение азимутов и поэтому для построения планов используют дирекционные углы.

  Х

Х (С) Х (С) Х (С) С g

Рис.9.1 Зависимость между прямым Рис.9.2 Зависимость между прямым

и обратным дирекционными углами и обратным истинными азимутами

a_АВ = a_ВА + 180°. А_АВ = А_ВА + 180° -g.

Из рис. 8.1 следует

А = a + g,

А = А_м+ d.

Приравняем правые части равенств

a+ g = А_м+ d или a = А_м+ d - g.

Зональное сближение меридианов g и магнитное склонение d для данной местности указывают на топографических картах местности.

Пусть имеем две стороны хода АВ и ВС (рис.10.1) Дирекционный угол стороны АВ будем считать известным. Если обозначить через b правый по ходу горизонтальный угол, то a_ВС = a_АВ + 180° - b.

N₀

Дирекционный угол последующего направления равен дирекционному углу предыдущего направления плюс 180 и минус горизонтальный угол справа по ходу.

Рис.10.1. Зависимость между дирекционными углами сторон хода

Предположим, что на местности проложен теодолитный ход между пунктами 512 и 513 (рис.10.2), начальный и конечный дирекционные углы в котором известны (a_511-512, a_513-Граб.).

Х

Грабово

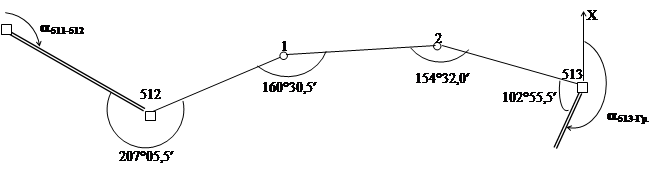Рис.10.2.Схема теодолитного хода

Уравнять (увязать) означает выполнить четыре действия:

1.Найти невязку f_b=П-Т,

где П - практическая сумма измеренных углов,

Т - теоретическое значение горизонтальных углов.

Для замкнутого теодолитного хода Т = Sb_теор = 180° (n-2),

для разомкнутого используем полученную раннее формулу a_ВС = a_АВ + 180° - b,

или перепишем ее в виде a_кон=a_нач + 180° - b_теор.

Из рис.10.2 имеем a_512-1= a_511-512 + 180° - b₅₁₂,

a_1-2 = a_512-1+ 180° - b₁,

a_2-513= a_1-2 + 180°- b₂,

a_513-Гр=a_2-513+ 180- b₅₁₃.

Откуда, теоретическая сумма горизонтальных углов Sb_теор = a_511-512 + 180°^. n - a_513-Гр.

Тогда можно записать в общем виде Т = Sb_теор = a_нач + 180°^. n - a_кон;

2.Оценить полученную невязку, т.е. сравнить с допустимым в соответствии с требованиями нормативных документов значением f_b < f_bдоп= 2tÖn, где n - число измеренных углов;

3. Распределить невязку с обратным знаком пропорционально числу измеренных углов с округлениями до 0,1. В углы с более короткими сторонами вводятся большие по величине поправки, так как они измеряются менее точно;

4.Выполнить контроль:

а)сумма поправок должна равняться невязке с обратным знаком;

б)сумма исправленных углов равна теоретической сумме углов.

а). Прямая

Х_В

Х

Дано: X_A, Y_A, a_AB, d_AB

В

Определить: X_B, Y_B.

Рис.11. Прямая и обратная геодезические задачи

Решение: X_B=X_A+d_AB^. cos a_AB=X_A+DX,

Y_B=Y_A+d_AB^. sin a_AB=Y_A+DY,

где DX и DY - приращения координат, т.е. проекции горизонтального проложения на соответствующие оси координат.

Контроль вычислений координат выполняют по формуле

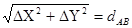
б). Обратная геодезическая задача

Дано: X_A, Y_A, X_B, Y_B.

Определить: a_AB, d_AB.

Решение: a_AB - r = arctg (DY/DX),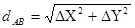

Контроль: d ^. cos a + X_A = X_B, d ^. sin a + Y_B = Y_B.

Примеры:

1. Определите координаты точки В, если X_A=Y_A=100м, a_AB=315°, d_AB=100м (sin 315° = -0,70711, cos 315° =0,70711).

Решение: X_B=X_A+d_AB ^. cosa_AB=170,71 м, Y_B=Y_A+d_AB ^. sin a_AB= 29,29 м.

2. Определите дирекционный угол направления ВС и горизонтальное проложение ВС, если XВ=YВ=1000м, XС=1100м, YС=900м.

Решение:

a_ВС® r_ВС=arctg{(Y_C-Y_B)/(X_C-X_B)}=45° СЗ, a_ВС=360° -45° =315°,

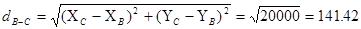м

Дата добавления: 2014-11-08