Перспектива окружности

Окружность в перспективе можно построить несколькими способами, из которых остановимся на двух.

Способ 1. Для построения перспективы окружности или любой другой кривой линии определяют перспективы достаточно большого числа её точек, которые соединяют плавной кривой. Перспективу каждой точки строят с помощью двух вспомогательных прямых или радиальным методом.

Способ 2. Около окружности или другой кривой описывают квадрат или

другой многоугольник; строят перспективу этого многоугольника и в него вписывают кривую, которая и будет являться перспективой заданной кривой.

Рассмотрим пример применения второго способа.

Задача 5.2. Построить перспективу окружности, расположенной в плоскости (рис. 5.2а). Положение точки зрения 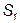, плоскости картины и высота горизонта (h-h) заданы.

Решение:

1. Описываем вокруг окружности квадрат 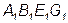, стороны которого соответственно параллельны и перпендикулярны картине (рис. 5.2а). Из 8 точек, которые показаны на рис. 5.2а, четные расположены на серединах сторон квадрата, нечетные – на его диагоналях. Заметим, что середины сторон, перпендикулярных к картине, определены с помощью прямой, которая проходит через центр симметрии квадрата (точку пересечения диагоналей).

2. Вершины и квадрата соединяем с точкой стояния .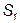

3. Изображение картины выполняем с увеличением линейных размеров в два раза.

Рис. 5.2

Для построения перспективы квадрата переносим с ортогонального чертежа (рис. 5.2а) на основание картины (рис. 5.2б) с учетом масштаба точк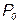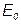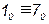и , , , , и (картинные следы вспомогательных прямых).

4. Все точки кроме 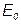и соединяем с главной точкой Р картины.

5. Через точк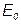и и проводим прямые, перпендикулярные к основанию картины и в их пересечении с прямой , определяем перспективы и 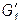вершин квадрата.

6. Через эти точки проводим прямые, параллельные основанию картины, в пересечении которых с прямой 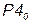определяем перспективы точек и - двух других вершин квадрата. Дальнейшие построения в перспективе выполняются, как показано на рис.5.2б.

7. Выполненные построения дают 8 точек, принадлежащих окружности, через которые следует провести кривую, представляющую собой эллипс.

Дата добавления: 2014-11-08