Постановка и решение задач

А В С D

Вопросы

1. Что такое калькуляция?

2. Каковы основные возможности электронных таблиц?

3. Какие электронные таблицы используются на IBM PC?

4. Как записываются формулы в электронных таблицах?

5. Какие математические функции есть в электронных таблицах?

6. Какие диаграммы есть в электронных таблицах?

Задания

1. Составьте систему формул для расчета заработной платы по следующей таблице:

	фамилия	часы	оплата	з/плата
	Иванов
	Петрова
	Сидоров
			итого:

2. Составьте калькуляцию для закупок письменных принадлежностей:

	А	В	С	D	Е	F
	Закупки:	цена	колич	сумма
	тетради
	карандаши
	ручки
	ластики
			всего:

3. Составьте калькуляцию закупок продуктов для похода на N дней и М человек.

4. Постройте на экране по таблице закупок:

а) круговую диаграмму;

б) график роста затрат;

в) плоскую гистограмму;

г) объемную гистограмму.

Решение задач состоит в получении определенных результатов. Это относится к работе, жизни или учебе: сдача экзаменов, написание сочинений, выполнение чертежей, изготовление приборов, инструментов и машин, сбор урожая, накопление капитала — все это получение результатов.

Ключом к любой задаче является способ решения, дающий необходимые результаты. Знание способов решения и умение их применять для решения практических задач — важнейшая характеристика профессиональной квалификации.

Результаты правильные, если они отвечают требованиям решаемых задач. Однако если требования неизвестны или сформулированы недостаточно четко, то нельзя однозначно судить о правильности полученных результатов.

Результаты неправильные, если они противоречат заданным требованиям. Как однозначно определить правильность результатов? Ответ: для этого необходима точная постановка задач с четким выделением требований.

Для решения задач необходимо определение:

1) что требуется?

2) что дано?

Ответ на первый вопрос — что требуется? — точное определение требуемых результатов. При отсутствии требований к конечным целям оценка полученных результатов может быть неоднозначной.

Ответ на второй вопрос — что дано? — определение исходных условий, при которых требуется получить результаты. Неоднозначность в определении исходных условий может привести к получению неправильных результатов.

Рассмотрим задачу: «Добраться домой». Исходным будет место, где мы находимся, а требуемым — свой дом. Способов решения этой задачи может быть много, но правильные среди них только те, которые обеспечат достижение своего дома.

Рассмотрим вторую задачу: «Решение уравнения 2 ∙ х + 1 = 0». Здесь требуемым является корень уравнения. В качестве решения уравнения можно рассмотреть два числа х₁ = 1 и х₂ = —1/2. Правильным из них является то решение, при подстановке которого уравнение превратится в тождество.

Подстановка первого числа х₁ = 1 в уравнение дает противоречие

2 ∙ (1) +1 = 3 ≠ 0.

Следовательно, значение х₁ = 1 — это неправильное решение, так как оно противоречит требованиям и не может быть корнем уравнения.

Подстановка второго решения х₂ = —1/2 в уравнение дает тождество

2 ∙ (-1/2) +1 = 0.

Таким образом, значение х₂ = —1/2 удовлетворяет исходному уравнению и является правильным решением.

Способ решения правильный, если он дает правильные результаты. Для определения правильности способов решения задач необходима четкая постановка решаемых задач, в которых должны быть строго определены требуемые результаты.

Способ неправильный, если его применение приводит к получению неправильных результатов либо вовсе не дает никаких результатов. Использование неправильных способов решения может вообще не давать результатов.

Способы могут быть частными и общими. Частные способы дают конкретные решения частных задач. Частный способ может оказаться неприменимым для решения сходных задач, отличающихся деталями.

Общий способ может давать решения для целого класса задач, отвечающих определенным исходным условиям и отличающихся друг от друга конкретными исходными данными.

Так, для рассмотренной задачи решения уравнения 2 ∙ х + 1 = 0 можно использовать общий способ решения линейных уравнений вида а ∙ х + b = 0:

x₀ = -b/а.

Применение этой формулы при а = 2, b = 1 дает решение x₀ = -b/а = -1/2, которое нам уже известно как правильное.

В правильности общего способа решения уравнений вида а ∙ х + b = 0 можно убедиться подстановкой формулы x₀ = -b/а в само уравнение:

a ∙ x₀ + b = a ∙ (-b/a) + b = -b + b = 0.

При постановке обобщенных задач кроме выделения требуемого необходимо определить исходные условия, при которых должно быть получено требуемое. В такой постановке задач должно быть определено, какие исходные условия будут считаться допустимыми, а какие нет.

Постановка задачи:

1. Что дано?

2. Что требуется?

3. Что допустимо?

Приведем полное описание постановки рассмотренной выше задачи.

Задача: решить уравнение а ∙ х + b = 0.

Треб.: х — корень уравнения.

Дано: а, b — коэффициенты уравнения.

При: а ≠ 0.

Уравнения данного типа можно решать в общем виде с помощью электронных таблиц, применяя описанный общий метод решения и следующую калькуляцию:

	А	В	С	D
		уравнение:
		* х +		= 0
	корень:	х =	-0.5

с расчетной формулой С3 = -С2 / А2.

Особую ценность для решения задач представляют обобщенные методы решения. Метод — единый способ решения некоторого класса задач. Знание методов позволяет находить решения для любой конкретной задачи данного класса.

Метод решения — правильный, если он дает правильные результаты для любой задачи данного класса. Применение таких методов гарантирует правильность результатов для любой задачи данного класса.

Метод решения — неправильный, если можно указать конкретную задачу данного класса, для которой применение метода даст неправильные результаты либо не даст результатов вовсе.

Например, для уравнения а ∙ х + b = 0 формула х = —b/а не дает результата при а = 0. Но при значении а = 0 уравнение превращается в соотношение b = 0, что говорит о недопустимости этого значения. Следовательно, условием допустимости данных в рассматриваемой задаче будут значения а ≠ 0.

Правильность методов решения можно и нужно проверять на конкретных примерах, подтверждающих правильность получаемых результатов. Однако достаточно привести хотя бы один контрпример, чтобы утверждать о неправильности метода решения в целом.

И все-таки демонстрация правильности результатов на двух-трех конкрентных примерах не может служить достаточным основанием для утверждений о правильности метода или способа решения в целом.

Полное обоснование правильности методов решения дает только исчерпывающий анализ результатов, получаемых для любой из задач данного класса. Пример — приведенное выше обоснование общего метода решения линейных уравнений.

В общем случае обоснование правильности обобщенных методов решения требует исчерпывающего математического исследования получаемых результатов и математического доказательства их правильности для всех конкретных случаев.

В качестве примера проведем анализ правильности метода вычисления средних значений последовательностей чисел:

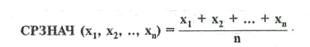
Для определения средних значений с помощью ЭВМ обычно используют следующую рекуррентную схему вычислений:

s₁ = х,

{s_k = s_k-1 (k-l) / k + x_k / k, (k = 2, 3,.., n)

СРЗНАЧ = s_n

Действительно, для k = 1 имеем:

s₁ = х₁.

Для k = 2 из рекуррентной формулы получим:

s₂ = s₁ (2 - 1) / 2 + х₂ / 2 = s₁ / 2 + х₂ / 2 = x₁ / 2 + х₂ / 2 = (x₁ + х₂) / 2.

Для k = 3 из этой же рекуррентной формулы получим:

s₃ = s₂ (3-1) / 3 + x₃ / 3 = s₃ 2/3 + x₃ / 3 = (x₁ + x₂) / 2) / 2 / 3 + x₃ / 3 = (х₁ + х₂ + x₃) / 3.

На основе приведенных формул можно сделать заключение о том, что для произвольного k будет выполняться соотношение

s_k = (х₁ + х₂ +... + х_k) / k.

В самом деле, допустим, что это соотношение верно для k—1:

s_k-1 = (х₁ + х₂+ … + x_k-1) / (k-1)

Тогда из рекуррентной формулы получим:

s_k = S_k-1(k - l) / k + х_k / k = [(x₁ + x₂ +... + x_k-1) / (k - l)] (k - l) / k + x_k / k = (x₁ + x₂ +... + x_k-1) / k + x_k / k = (х₁ + x₂ +... + х_k-1 + x_k) / k.

Таким образом, на каждом шаге k = 1, 2, 3,... рекуррентная формула дает среднее арифметическое значение обработанной последовательности чисел. Тогда на основании математической индукции можно утверждать, что на последнем шаге вычислений при k = n будет вычислено среднее арифметическое значение:

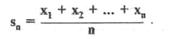
Что в требовалось доказать.

Дата добавления: 2014-11-25