Что и требовалось

Кон

Кон

Кесли

Кон

Кесли

Нач

Кон

Нач

Кон

Нач

v:= х×х v₁ = х×х Þ v₁ = x²

v:= v×v v₂ = v₁×v₁ Þ v₂ = x⁴

у:= v×x у = v₂×x Þ у = х⁵

Справа от алгоритма приведены результаты выполнения присва­иваний. Результатом первого присваивания v:= х×х будет значение v₁ = х×х переменной v. Результат следующего присваивания v:= v×v - второе значение переменной v, равное v₂ = v₁×v₁. Результатом треть­его присваивания у:= v×x будет значение у = v₂×x.

На основе приведенных рассуждений, можно сделать три утверж­дения о промежуточных и конечных результатах вычислений:

РезультатыУтверждения

{ v₁ = х×х Þ v₁ = х²

{ v₂ = v₁×v₁ Þ v₂ = x⁴

{ у = v₂×x Þ у = х⁵

Таким образом можно высказать окончательное

Утверждение. Конечным результатом выполнения будет

у = х⁵ для любых значений х.

Доказательство. Исходя из описания результатов выполнения присваиваний значение у будет равно

у = v₂×x = (v₁×v₁)×x = ((х × х).(х × х))) × х = x⁵.

Что и требовалось доказать.

Техника анализа и доказательства правильности алгоритмов и программ во многом совпадает с техникой доказательства любых других утверждений и состоит в применении следующих четырех приемов:

· разбор случаев;

· подбор контрпримеров;

· выделение лемм;

· индуктивный вывод.

Разбор случаев применяется для анализа результатов выполнения конструкций альтернативного выбора. В качестве примера проведем анализ приведенного выше алгоритма «выбора» максимума трех чисел, содержащего выбор альтернатив.

алг «у = тах(а, b,с)» Результаты

если а > b то при а > b

у:= а у = а

инес b > с то при b > с

у:= b у = b

инес с > а то при с > а

у:= с у = с

кесли при не (b > с)

Справа от алгоритма приведены результаты вычислений с указа­нием условий, при которых они получаются. На основании этих фактов можно заключить, что конечные результаты вычисления имеют три варианта:

а, при а > b,

у = b, при b > с и b ³ а,

с, при с > а и с ³ b.

В то же время значение максимума должно быть равно:

а, при а ³ b и а ³ с,

mах = b, при b ³ с и b ³ а,

с, при с ³ а и с ³ b.

Во всех трех случаях видны различия в условиях получения и определения максимальных значений. Покажем, что эти различия существенны и утверждение о том, что алгоритм дает правильные результаты для всех данных, неверно.

Для опровержения общего утверждения достаточно указать хотя бы один контрпример. В данном случае утверждение о правильности алгоритма гласило бы: для любых значений переменных а, b, с конечным было бы значение mах (а, b, с).

Контрпримером в данном случае будут значения: а = 2, b = 1, с = 3. Для этих данных по определению mах = 3, а по результатам выполнения алгоритма у = 2. Следовательно, в алгоритме содержится ошибка.

Однако оказывается, что это не единственная ошибка. Более тон­кие ошибки вскрывает второй контрпример: а = 1, b = 1, c = 1. Для этих данных в алгоритме вовсе не определен результат вычислений у =? и конечный результат выполнения программы будет непред­сказуем!?

Правильное решение этой задачи можно получить применением систематических методов, составив постановку и описание метода решения.

Постановка задачиМетод решения

Вычисление mах (а, b, с).

Дано: а, b, с - три числа. mх = mах(mах(а,b),с)

Треб.: mх – максимум. mах(х,у) = х, при х ³ у

Где: mх = mах (а, b, с). у, при у ³ х

Данный метод решения непосредственно состоит из формул определения максимумов из трех и двух чисел. Реализация этого метода в форме алгоритма может быть такой:

алг «тх = тах(а,b,с)» Результаты

если а ³ b то при а ³ b

тх : = а mx = a

иначе при b > а

mх : = b mх = b

кесли { mх = mах(а,b) } при с < mх

если с ³ mх то при с ³ mх

mх:= с mх' = с

Доказательство правильности алгоритмов можно проводить двумя способами. Первый способ - анализ правильности при по­строении алгоритмов. Второй способ - анализ правильности после построения алгоритмов.

Первый способ - показать, что алгоритм является корректной реализацией метода решения, и доказать, что метод - правильный. Для рассмотренного алгоритма это доказательство изложено выше.

Привлечение для создания алгоритмов известных методов реше­ния, для которых доказана их правильность, позволяет существенно упростить обоснование правильности программ. При этом центр тяжести проблем смещается к созданию и обоснованию гарантиро­ванно правильных методов решения задач.

Второй способ - исчерпывающий анализ результатов выпол­нения алгоритма на соответствие постановке решаемых задач для любых допустимых данных. Это - доказательство путем исчерпыва­ющего анализа результатов выполнения алгоритмов и программ.

Результаты выполнения рассматриваемого алгоритма вычисления максимума трех чисел приведены справа от него. Анализ результатов алгоритмов, содержащих конструкцию выбора, требует разбора случаев. Отметим, что все эти случаи были уже указаны ранее при разборе ошибочной версии алгоритма.

Для обоснования правильности алгоритма докажем вспомогатель­ное утверждение о результатах выполнения конструкции альтерна­тивного выбора.

Лемма: Конечными результатами выполнения алгоритма

АлгоритмРезультаты

если а > b то при а ³ b

тх := а mx = a

иначе при b > a

тх:= b mx = b

является значение mx = max(а, b) для любых значений а и b.

Доказательство. Результатом вычислений здесь будут значения

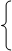а при а ³ b

mx =

b при а < b

что совпадает с определением max (а, b).

С помощью этой леммы легко доказать правильность алгоритма в целом.

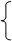{ mх = max (а, b) } Результаты

если с ³ mx то при с ³ mx

mx:= с mx' = с

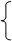кесли mx' = mx

при с < mx

Утверждение. Конечным результатом выполнения алгоритма вы­числения максимума будет значение mx' = max (а, b, с) для любых значений а, b и с.

Доказательство. В силу предположения предшествующее значе­ние переменной mx = max(a,b). Отсюда получаем, что

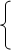с, при с ³ mx

mx¢ = = max(a,b,c).

mx, при с < mx

Что и требовалось доказать.

Доказательство лемм - основной прием доказательства правиль­ности сложных алгоритмов и программ. Напомним, что лемма — это вспомогательное утверждение, предполагающее отдельное доказа­тельство.

Одним из важнейших применений аппарата лемм является анализ результатов выполнения и доказательство правильности алгоритмов с циклами. Используемые для анализа циклов леммы называются индуктивными утверждениями. Эти леммы выражают утверждения о промежуточных результатах выполнения циклов.

В качестве примера использования индуктивных рассуждений рассмотрим алгоритм вычисления среднего арифметического после­довательности чисел. В приводимом алгоритме предполагается, что последовательность чисел размещена в массиве X[1:N].

алг «среднее значение»

массив X[1:N]

нач Результаты:

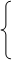от k = 1 до N цикл

S:= S * (k-l)/k + X[k]/k S_k = S_k-1*(k-l)/k + X[k]/k

кцикл [k = (1...N)]

Xcp:= S Xcp = S

Этот алгоритм обычно считается ошибочным (?!). «Ошибкой» в этом алгоритме считается отсутствие присваивания S:= 0 перед началом цикла.

Разберем результаты выполнения алгоритма на первых трех ша­гах:

S₁ = S₀×(l - 1)/1 + Х[1]/1 = S₀×0/1 + Х[1]/1 = Х[1]/1;

S₂ = S₁×(2 - 1)/2 + Х[2]/2 = S₁×1/2 + Х[2]/2 = Х[1]/2 + Х[2]/2;

S₃ = S₂×(3 - 1)/3 + Х[3]/3 = S₂×2/3 + Х[3]/3 = Х[1]/3 + Х[2]/3 + Х[3]/3.

Можно утверждать, что на первых трех шагах результатом является среднее арифметическое обрабатываемых чисел. На основе этих примеров можно сделать индуктивное утверждение - «на каждом очередном k-м шаге выполнения цикла результатом будет среднее арифметическое»

S_k = S_k-1×(k-l)/k + X[k]/k = X[l]/k + X[2]/k +... + X[k]/k.

Доказательство этого утверждения проводится с помощью мате­матической индукции. На первом шаге при k = 1 оно уже доказано. Допустим, что оно справедливо на (k -1)-м шаге

S_k-1 = X[l]/(k-l) + X[2]/(k-l) +... + X[k-l]/(k-l).

Подставим его в описание результатов цикла на k-м шаге

S_k= S_k-1×(k-l)/k +X[k]/k.

Тогда результат выполнения цикла на k-м шаге оказывается рав­ным

S_k = X[l]/k + X[2]/k +... + X[k-l]/k + X[k]/k,

т. е. среднему арифметическому первых k чисел.

Таким образом, индуктивное утверждение доказано. В силу мате­матической индукции это утверждение верно для всех k = l, 2,..., N. Следовательно, на последнем шаге конечным результатом выполнения цикла станет значение

S_N = S_N-1×(N-1) + X[N]/N = X[1]/N +... + X[N]/N.

Исходя из этого утверждения конечным результатом выполнения алгоритма в целом будет среднее арифметическое значение

Xcp = S_N = X[1]/N +... + X[N]/N.

Следовательно, приведенный алгоритм, несмотря на содержа­щуюся в нем «ошибку», является правильным. В целом анализ правильности алгоритмов с циклами во многом построен на исполь­зовании индукции.

Индукция - это вывод общих суждений из частных примеров. При анализе циклов она используется для подбора индуктивных утверждений о промежуточных результатах выполнения циклов. Однако для доказательства правильности индуктивных утверждений о результатах выполнения циклов используется полная математи­ческая индукция.

Математическая индукция - это принцип доказательства после­довательностей утверждений Р(1), Р(2), Р(3),..., P(N),.... когда известно, что верны первые утверждения для n = 1, 2, 3 и из истин­ности (n - 1)-го утверждения следует истинность n-го утверждения:

Принцип математической индукции: если первое утверждение Р(1) истинно и из утверждения Р(n - 1) следует утверждение Р(n), то истинны все утверждения Р(1), Р(2), Р(3),..., Р(n),....

Приведем примеры индуктивного анализа циклов для алгоритма нахождения минимального значения в последовательности чисел, который в этот раз действительно будет ошибочным.

алг «нахождение минимума»

массив x[1:N]

нач Результаты:

от k = 1 до N цикл

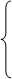если x[k] < min то

тп:= x[k] mn_k = { x[k], при x[k] < mn_k-1

все { mn_k-1, в ином случае

кцикл [ k = (1... N)]

Min:= тп Min = mn_N

Утверждение. Приведенный алгоритм определения минимального значения последовательности чисел неправильный.

Доказательство. Для демонстрации ошибок необходимо привести контрпример. Для построения контрпримера разберем результаты выполнения на первом шаге цикла.

Результаты выполнения первого шага цикла при k = 1:

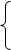х[1] при х[1] < mn₀

mn₁ = = min (х[1], mn₀).

mn₀ при х[1] £ mn₀

Следовательно, результатом будет

mn₁ = min (x[l], mn₀).

Однако поскольку начальное значение mn₀ неизвестно, то не­определено значение результата выполнения первого шага цикла. Аналогичное утверждение можно сделать о втором и всех последу­ющих шагах выполнения цикла:

mn_k = min (x[k], Min(x[k-l],..., х[1], mn₀) = Min (x[k], x[k-1],..., х[1], mn₀).

В силу математической индукции это утверждение справедливо при k = N:

mn_N = Min (x[N], x[N - 1],..., x[2], х[1], mn₀).

Таким образом на основании этого утверждения можно сделать заключение о конечном результате выполнения алгоритма в целом:

Min = mn_N = Min (x[N], x[N - 1],..., x[2], х[1], mn₀).

Из этой формулы видно, что конечный результат равно как и результат первого присваивания зависит от начального значения mn₀ переменной mn. Однако эта величина не имеет определенного значения, соответственнно неопределен и конечный результат выполнения алгоритма в целом, что и является ошибкой.

В самом деле, если значение mn₀ окажется меньше любого из значений последовательности х[1],.... x[N], то конечный результат вычислений будет неправильным. В частности, при реализации алгоритма на Бейсике неправильный результат будет получен, если последовательность будет состоять только из положительных чисел. Например, для последовательности чисел: 1, 2, 3,..., N.

Приведем правильную версию алгоритма с доказательством отсутствия ошибок, используя технику индуктивных утверждений.

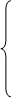алг «нахождение минимума» массив х[1:п] нач тп:= x[1] от k = 1 до N цикл если x[k] < тп то тп = x[k] все кцикл Min = тп кон

Результаты: mn0 = х[1] [k = (1... N)] 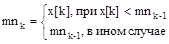Min = mnN

Утверждение. Для любой последовательности чисел x[l:N] конечным результатом вычислений будет значение Min = Min (х[1],..., x[N]).

Доказательство. Воспользуемся результатами анализа выполнения алгоритма, рассмотренного ранее. Различие между ними состоит в добавлении перед началом цикла присваивания mn:= х[1], которое задает начальное значение переменной mn, равное mn₀ = х[1].

Тогда в силу приведенных ранее рассуждений и выкладок ко­нечным результатом выполнения новой версии алгоритма будет значение

Min = mn_N = Min(x[N], x[N-l],..., х[2], х[1], mn₀) =

= Min(x[N], x[N-l],..., x[2], x[l], x[l]) = Min(x[N],.... х[1]).

Рассмотренные примеры являются образцами доказательств пра­вильности алгоритмов и программ, которые могут использоваться для анализа и доказательства правильности других новых алгоритмов и программ обработки данных.

Общий вывод, который мы хотим сделать, состоит в том, что применение доказательных методов превращает программирование в научную дисциплину создания безошибочных алгоритмов и надеж­ных программ для ЭВМ.

Дата добавления: 2014-11-25