Общая система уравнений подземной гидромеханики

Скорость фильтрации

При исследовании фильтрационных течений удобно отвлечься от размеров пор и их формы, допустив, что флюид движется сплошной средой, заполняя весь объём пористой среды, включая пространство, занятое скелетом породы.

Предположим, что через поверхность F пористой среды протекает объёмный расход флюида

Q=`w F_п, (2.1)

где `w – действительная средняя скорость жидкости; F_п – площадь пор.

Площадь пор связана с полной поверхностью через просветность (соотношение 1.2), а для сред неупорядочной структуры справедливо допущение о равенстве просветности и пористости. Следовательно,

Q=`w m F. (2.2)

Величина

u= `w m (2.3)

называется скоростью фильтрации и определяет переток флюида, осреднённый по площади. Так как m<1, то скорость фильтрации всегда меньше средней.

Физический смысл скорости фильтрации заключается в том, что при этом рассматривается некоторый фиктивный поток, в котором:

· расход через любое сечение равен реальному расходу,

· поле давлений идентично реальному потоку,

· сила гидравлического сопротивления равна силе сопротивления реального потока.

Предполагается, что скорость фильтрации непрерывно распределена по объёму и связана со средней действительной скоростью течения равенством (2.3).

Для нестационарного процесса при отсутствии источников и стоков имеем:

· уравнение неразрывности

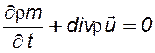; (2.4)

· уравнение сохранения количества движения

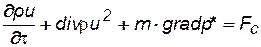. (2.5)

В уравнении (2.5):

· в виду незначительности изменения количества движения во времени первым членом можно пренебречь;

· разница в перетоках количества движения через границы контрольных объёмов также составляют величины второй малости по сравнению со скоростями и, следовательно, вторым членом тоже можно пренебречь;

· силу сопротивления F_c по аналогии с трубной гидравликой или задачами обтекания можно представить в виде

.

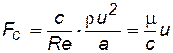Таким образом, уравнение (2.2) вырождается в следующее

,

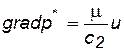то есть, получаем уравнение, линейно связывающее скорость фильтрации с градиентом давления.

Уравнение такого вида широко используется в подземной гидродинамике и носит название уравнения фильтрации в форме Дарси:

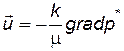, (2.6)

где р*=р+z r g, z – вертикальная координата.

Движение жидкости может быть установившимся (стационарным) и неустановившимся (нестационарным). При установившемся движении параметры потока (плотность, скорость фильтрации и так далее) в каждой точке пористой среды постоянны и не зависят от времени. Таким образом, для установившейся фильтрации 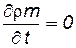и уравнение неразрывности принимает вид

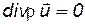. (2.7)

В вышеприведенных уравнениях:

;

;

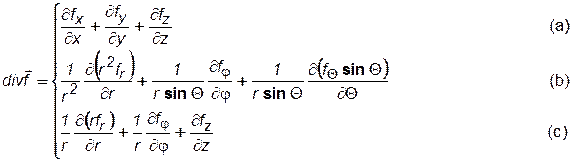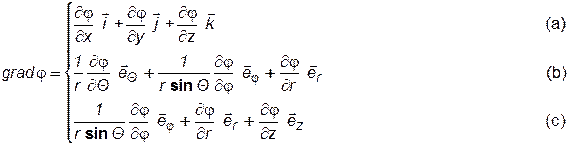(a) – декартовые координаты; (b) – сферические координаты; (c) – цилиндрические координаты; i, j, k – единичные векторы по осям декартовой системы координат; e _Q, e _j, e_r, e_z – по осям сферической системы; Q, j, r и z – по осям цилиндрической системы; в сферических координатах – угол Qопределяет изменение меридианного угла, а угол j – широтного.

Для несжимаемой жидкости ( r =сonst) уравнение (2.3) запишется в виде

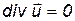. (2.8)

2.3. Закон Дарси (линейный закон фильтрации)

Дата добавления: 2014-11-25