Правила изображения схем алгоритма и записи псевдокодов

Изображение схем алгоритмов осуществляют согласно ГОСТ 19.701–90, в котором каждой группе действий ставится в соответствие блок особой формы. Некоторые, часто используемые обозначения приведены в таблице 1.

Таблица 1

Название блока	Обозначение	Назначение блока
1. Терминатор		Начало, завершение программы или подпрограммы
2. Процесс		Обработка данных (вычисления, пересылки и т.п.)
3. Данные		Операции ввода-вывода
4. Решение		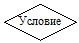Ветвления, выбор, итерационные и поисковые циклы
5. Подготовка		Счетные циклы
6. Граница цикла		Любые циклы
7. Предопределенный процесс		Вызов процедур
8. Соединитель		Маркировка разрывов линий
9. Комментарий		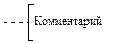Пояснения к операциям

При разработке схемы алгоритма каждое действие обозначают соответствующим блоком, показывая их последовательность линиями, идущими слева направо и сверху вниз. Для удобства чтения схемы желательно, чтобы линия входила в блок сверху, а выходила снизу. Если направление линии отлично от стандартного, то в конце линии ставится стрелка, в противном случае стрелку можно не ставить.

Если схема алгоритма не умещается на листе, то используют специальные соединители. При переходе на другой лист или получении управления с другого листа в комментарии указывают номер листа, например, «с листа 3», «на лист 1».

Доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых управляющих структур:

· следование – обозначает последовательное выполнение действий (см. рисунок 3, а);

· ветвление – соответствует выбору одного из двух вариантов действий (см. рисунок 3, б);

· цикл-пока – определяет повторение действий, пока не будет нарушено некоторое условие, выполнение которого проверяется в начале цикла (см. рисунок 3, в).

Рисунок 3 – Базовые алгоритмические структуры: следование (а), ветвление (б) и цикл-пока (в)

Помимо базовых структур используют еще три дополнительные структуры, производные от базовых:

· выбор – обозначающий выбор одного варианта из нескольких в зависимости от значения некоторой величины (см. рисунок 4, а);

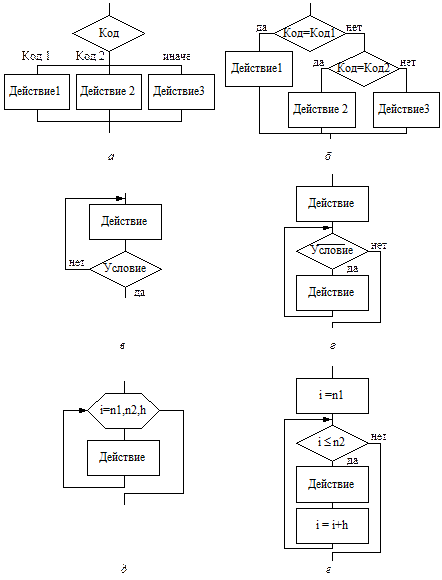
Рисунок 4 - Дополнительные структуры и их реализация через базовые структуры: выбор (а-б), цикл-до (в - г) и цикл с заданным числом повторений (д - е)

· цикл-до – обозначающий повторение некоторых действий до выполнения заданного условия, проверка которого осуществляется после выполнения действий в цикле (см. рисунок 4, в);

· цикл с заданным числом повторений (счетный цикл) – обозначающий повторение некоторых действий указанное количество раз (см. рисунок 4, д).

На рисунке 4 (б, г и е) показано, как каждая из дополнительных структур может быть реализована через базовые структуры.

В том случае, если в схеме алгоритма отсутствуют другие варианты передачи управления, алгоритм называют структурным, подчеркивая, что он построен с учетом рекомендаций структурного программирования.

Помимо детальных схем алгоритма допустимы обобщенные схемы, на которых группы действий изображают в виде подпрограмм.

Псевдокод базируется на тех же основных структурах, что и структурные схемы алгоритма. Описать на псевдокоде неструктурный алгоритм нельзя.

Для каждой структуры используют свою форму описания. В литературе были предложены несколько вариантов псевдокодов. Один из них приведен в таблице 2.

Таблица 2

Структура	Псевдокод	Структура	Псевдокод
1. Следование	<действие 1> <действие 2>	4. Выбор	Выбор <код> <код1>: <действие 1> <код2>: <действие 2> ... Все-выбор
2. Ветвление	Если <условие> то<действие 1> иначе<действие 2> Все-если	5. Цикл с заданным количеством повторений	Для<индекс> = <n>,<k>,<h> <действие> Все-цикл
3. Цикл-пока	Цикл-пока<условие> <действие> Все-цикл	6. Цикл-до	Выполнять <действие> До<условие>

Пример 2. Разработать алгоритм определения наибольшего общего делителя двух натуральных чисел.

Существует несколько способов определения наибольшего общего делителя двух натуральных чисел. Самым простым из них является так называемый «алгоритм Евклида». Суть этого метода заключается в последовательной замене большего из чисел на разность большего и меньшего. Вычисления заканчиваются, когда числа становятся равны.

Например:

а)	A B	б)	A B
	225 125		13 4
	225-125=100 125		13-4=9 4
	100 125-100=25		9-4=5 4
	100-25=75 25		5-4=1 4
	75-25=50 25		1 4-1=3
	50-25=25 = 25		1 3-1=2
			1 = 2-1=1

Программа должна начинаться с ввода чисел. Заметим, что любой ввод данных пользователем должен сопровождаться запросом на ввод, чтобы пользователь знал, чего от него ждет программа после запуска. На схеме алгоритма и при записи псевдокодов этот запрос обычно не указывают.

В основе алгоритма лежит циклический процесс, количество повторений которого заранее неизвестно (итерационный). Условие выхода из цикла – получение одинаковых чисел. Поскольку нельзя исключить, что пользователь введет равные числа, проверку будем осуществлять на входе в цикл, т. е. имеет смысл использовать цикл-пока. Если числа не равны, то при каждом проходе цикла большее из чисел должно заменяться разностью большего и меньшего. Для реализации этой замены потребуется описать оба варианта, т.е. использовать ветвление с проверкой, какое из чисел больше. После выхода из цикла числа равны, поэтому можно выводить пользователю любое из двух полученных чисел. На рисунке 5 показана схема алгоритма, а ниже приведено его описание на псевдокоде.

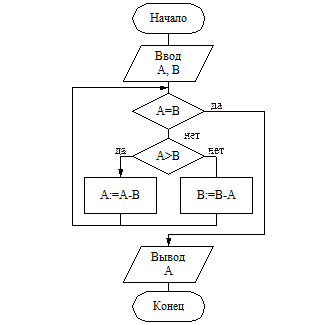
Рисунок 5 - Схема алгоритма Евклида

Алгоритм Евклида:

Ввести A,B

цикл-пока A¹B

если A>B

то A:=A-B

иначе B:=B-A

Дата добавления: 2014-11-25