Краткие сведения для решения задач 1 страница

ДИНАМИКА

Динамика точки.

Основное уравнение динамики материальной точки D массой m, движущейся с ускорением a под действием системы сил относительно инерциальной системы отсчёта XYZ (смотри рисунок 31) имеет вид

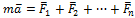, или ,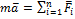

или в проекциях на оси X,Y,

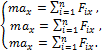
если учесть, что проекция ускорения на ось равна второй производной по времени от координаты точки по этой оси, т.е.

то получим три дифференциальных уравнения второго порядка

С помощью этих дифференциальных уравнений решаются две основные задачи динамики:

Первая задача: по заданным кинематическим уравнениям движения (, ) материальной точки и её массе найти равнодействующую сил, приложенных к точке.

Вторая задача: зная силы, приложенные к материальной точке и её массу, определить закон движения её (кинематические уравнения движения) и характеристики этого движения (скорость, ускорение и т.д.).

Вторая задача решается последовательным интегрированием каждого из трёх дифференциальных уравнений второго порядка. При этом (если берутся неопределённые интегралы) появляются по два постоянных интегрирования на одно уравнение. Их необходимо определить, используя, так называемые, начальные условия: в начальный момент (t₀) времени(обычно t₀ =0) должны быть известны положение точки (её координаты x₀, y₀, z₀) и её скорость V₀ (заданная через проекции на оси координат V_0X, V_0Y, V_0Z).

Задача 6 (Д1). Тема: Основная (вторая) задача динамики материальной точки.

Задание: Тело D массой m пришло в движение из точки А с начальной скоростью V_O (см. рис. 32). На участке АВ на тело действуют сила тяжести и сила трения (f=0,1). В точке В тело переходит на участок ВС, где на него, кроме силы тяжести и силы трения, действует переменная сила

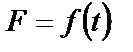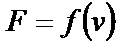(, или , или 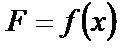), проекция, которой 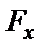задана в таблице 6. Считая тело материальной точкой, найти закон движения тела, зная расстояние АВ=l или время t₁ движения тела от точки А до точки В на участке ВС, т.е. 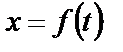, где х=ВД.

План выполнения задания.

Решение задачи разбивается на две части. Сначала надо составить и с учетом начальных условий проинтегрировать дифференциальные уравнения движения тела на участке АВ. Затем определить скорость тела в точке В, принимая во внимание, что точка В является начальной точкой движения тела по участку ВС. После этого надо составить и проинтегрировать дифференциальные уравнения движения тела на участке ВС так же с учетом начальных условий, ведя отчет времени от момента, когда тело находится в точке В, полагая, что в этот момент t=0.

Таблица 6

Вари- ант	m, кг	V0, м/с	l, м	t1, с	F x, H
				-	4 V
			-	3,5	9 t ^2
				-	6 x
	1,6		-		-4sin(2 t)
	1,8			-	-3,6 x
			-		2 V
	4,5			-	-2cos(2 t)
			-	2,5	-6 V
				-	4 t ^3
	0,6		-	1,5	12 x

Примеры

Решить указанную в задании задачу при следующих данных:

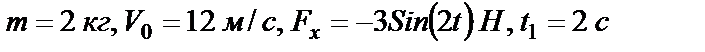, т.е. определяем .

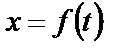I. Рассматриваем движение тела D на учачтке АВ, считая его материальной точкой D. Показываем в произвольном положении тело D и действующая на него силы: ‑ сила тяжести (); ‑ нормальная составляющая реакции поверхности по которой движется тело; 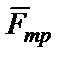‑сила трения.

Берем систему координат , совмещая начало координат с точкой А, из которой тело начинает движение: ось - направляем по движению тела; ось - направляем перпендикулярно к оси . К решению задачи применяем дифференциальные уравнения движения точки в проекциях на оси координат и .

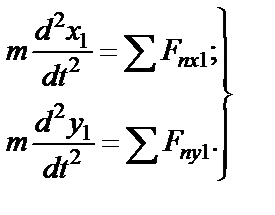
Для удобства составления этих уравнений вектор 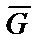разложим на два составляющих вектора 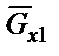и .

Составляем дифференциальные уравнения движения тела.

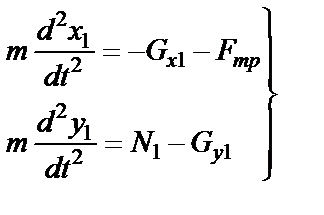, (20)

где .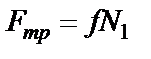

С учетом выражений для , , 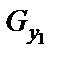, 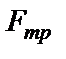уравнения (20) примут вид

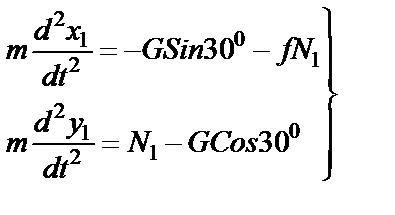(21)

Учитывая, что 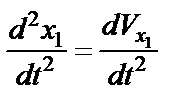, и , делаем замену.

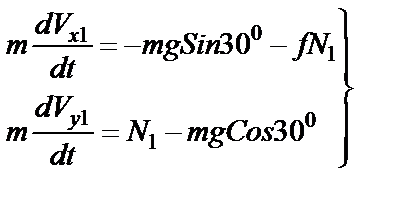(22)

Замечаем, что тело движется только по оси , поэтому

и значит, .

Делаем подстановку в первое уравнение из уравнений (22)

;

Упрощаем:

.

В числах:

Окончательно получим

(23)

Разделяем переменные и интегрируем:

Получаем:

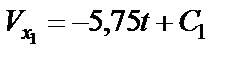(24)

Постоянную определяем по начальным условиям: при 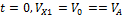,т.к. движение началось из точки А.

Подставляем в уравнение (24)

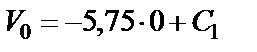, или ,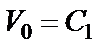

уравнение (24) принимает вид:

.

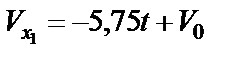Зная - время движения тела от точки А до точки В, определяем скорость тела в точке В

,

с учетом численных значений имеем

Если в условии задачи дано не время , а l – длина участка АВ, то уравнение (23) следует преобразовать так:

,

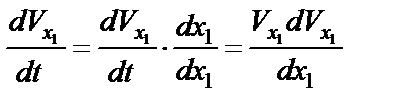окончательно

.

Затем разделяем переменные и проинтегрируем:

.

Получаем

,

Подставляем пределы интегрирования

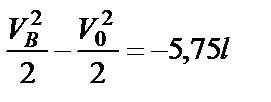
и находим скорость в точке В.

.

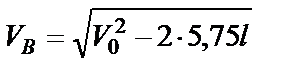Допустим 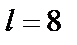м, тогда

.

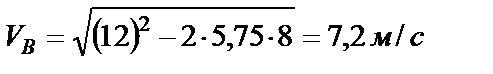II. Рассматриваем движение тела на участке ВС.

1. Случай, когда , а именно .

Показываем тело D в произвольном положении на участке BC и действующие на тело силы (см. рисунок 31): ­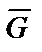 ‑ сила тяжести; ­ ‑ нормальная составляющая реакции связи; ­ ‑ сила трения; ­ ‑ заданная сила (проекция ­ ‑ отрицательная, поэтому силу 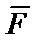направляем против движения).

Показываем систему координат 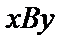с началом в точке В, ось Вх направляем по движению тела, ось Ву – перпендикулярно к Вх. Движение тела происходит только вдоль оси Вх, поэтому примем что

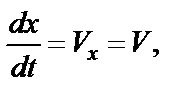а .

Составляем дифференциальные уравнения движения тела:

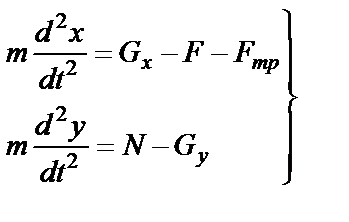, (25)

где

Учитывая, что = 0 (движение только по оси Вх), имеем .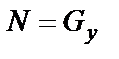

Делаем подстановку и решаем первое из уравнений (25)

или

После преобразования получим

В числах:

или окончательно

Разделяем переменные и интегрируем:

.

Получаем:

. (26)

Постоянную 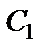определим по начальным условиям: при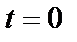

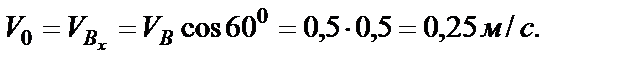
Подставляем и в уравнение (26)

,

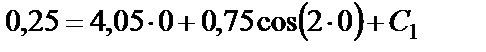откуда

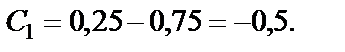
Подставляя значение в формулу (26), получаем закон изменения скорости

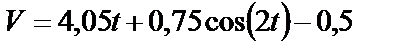. (27)

Делаем замену :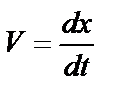

,

разделяем переменные и интегрируем

получаем:

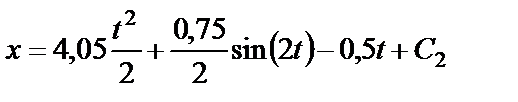. (28)

Постоянную 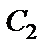определяем по начальным условиям: при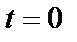 , подставляя их в выражение (28)

.

Откуда .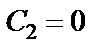

Окончательно имеем:

(29)

это и есть уравнение движения тела на участке ВС.

2. Случай, когда .

В рассматриваемом примере на участке ВС на тело действуют те же силы: 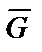, , ­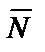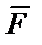, , где ­ . Допустим, что . Расстановка векторов сил и дифференциальные уравнения движения остаются те же, что и в случае .

, (30)

где силы 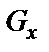, , определяются также как показано в случае 1.

Учитывая, что 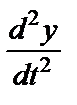= 0 (движение только по оси Вх), имеем .

Решаем первое из системы уравнений (30):

или

В числах:

после преобразования имеем

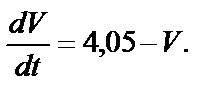
Разделяем переменные и интегрируем:

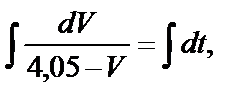
получаем

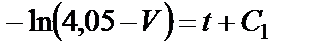. (31)

Постоянную определяем по начальным условиям: при подставляя их в выражение (31), откуда .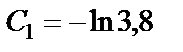

Теперь найденное значение 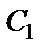используем в уравнении (31)

или

.

Решаем:

;

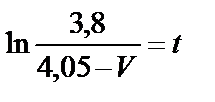после преобразования

,

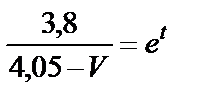или

,

откуда:

. (32)

С учетом выражение (32) примет вид

.

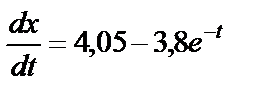Разделяем переменные и интегрируем:

.

Получаем:

(33)

Постоянную определяем по начальным условиям: при 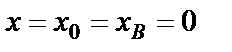, подставляя их в формулу (33)

,

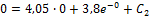откуда .

Уравнение движения тела на участке ВС

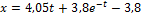(м)

3. Случай, когда на участке ВС на тело действует сила .

Допустим 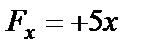, силу направим по движению тела.

Дифференциальные уравнения будут такие же, как и в рассмотренных выше случаях.

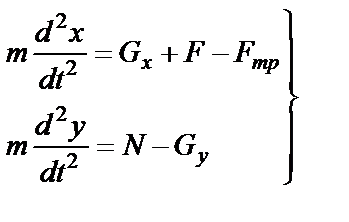, (34)

где силы , , 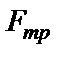по-прежнему определяются также как в случае 1

Учитывая, что 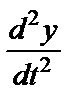= 0, упрощаем первое из уравнений (34):

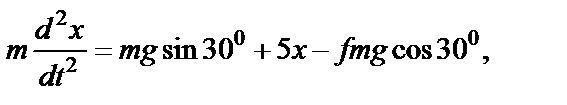
или

В числах:

окончательно

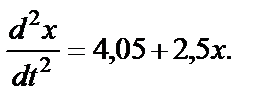
Запишем это уравнение так:

(35)

Введем обозначение: k²=2,5.

Уравнение (35) примет вид:

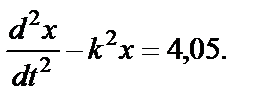
Согласно правилам математики, такое уравнение имеет решение в виде:

(36)

Постоянные и определяем по начальным условиям: при ;

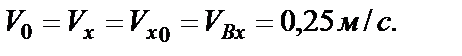
Для применения начальных условий находим уравнение скорости, продифференцировав по времени выражение (36)

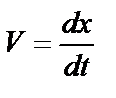
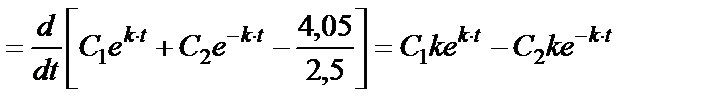. (37)

Введем в уравнения (36) и (37)указанные начальные условия и получим

,

и .

После преобразований имеем:

, (38)

. (39)

Из этих уравнений находим 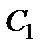и

. (40)

Подставим найденное для С₁ выражение(40) в формулу (38):

0=0,16+С₂+С₂ –1,62, или 0=2С₂ – 1,46,

откуда С₂= 0,73.

Тогда численное значение С₁ равно

С₁=0,16 + 0,73=0,89.

Подставляя найденные значения и в уравнение (36), находим уравнение движения тела на участке ВС.

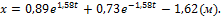
4. Случай, когда на участке ВС на тело действует сила .

Допустим . Дифференциальные уравнения будут такие же, как и в предыдущем случае, с той лишь разницей, что , а не 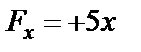. Силу направим против движения.

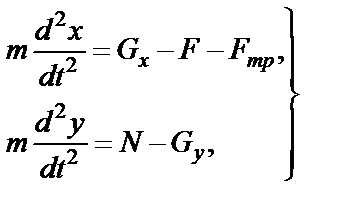(41)

где силы 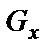, , находятся, как указано выше.

Делая замену как в предыдущем случае, получаем первое из уравнений (41) в следующем виде:

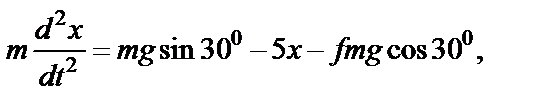
после преобразования:

С учетом численных значений известных величин (напомним,

что m=2 кг)

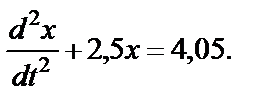(42)

Введем обозначение k²=2,5, тогда выражение (42) примет вид

Согласно правилам математики, такое уравнение имеет решение в виде:

, (43)

где ;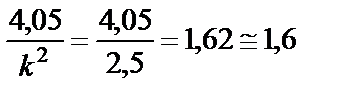

.

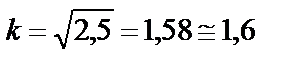Тогда уравнение (43) запишется так

. (44)

Чтобы применить начальные условия: пр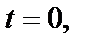и и для определения постоянных и , находим уравнение скорости

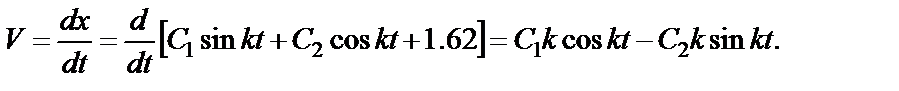(45)

Подставляем в уравнения (44) и (45) указанные начальные условия

0=C₁sink·0 + C₂cosk·0 + 1,62,

0,25= C₁ k cosk·0 - C₂ k sink·0.

После преобразований эти выражения примут вид

0= C₂+ 1,6,

0,25= C₁ k

Откуда находим С₁ и С₂

C₂=- 1,62,

C₁=0,25/k=0,25/1,58 0,16,

и, подставляя их значения в уравнение (44), получим уравнение движения тела на участке ВС.

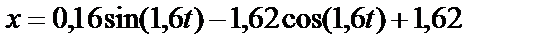(м).

Динамика механической системы (твёрдого тела).

Дата добавления: 2014-11-25