Вольт-амперная характеристика германиевого диода Д312А

В связи со слабым влиянием коллекторного напряжения на положение базовой характеристики в нормальном режиме работы транзистора (при) статические базовые характеристики, снятые при различных почти сливаются.

Семейство выходных ВАХ (рисунок 11) представляет собой зависимость тока коллектора от напряжения на коллекторе 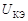при различных значениях тока базы :

.

Рисунок 11 – Семейство выходных ВАХ БТ для схемы

с общим эмиттером

Для входной цепи транзистора, то есть для тока базы, можно записать следующие уравнения:

.

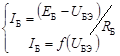Решение системы в графическом виде представлено на рисунке 11.

Оно представляет собой точку пересечения линий 1 и 2. Кривая 1 представляет собой входную ВАХ транзистора (второе уравнение системы) при условии, что напряжение достаточно велико и его влиянием можно пренебречь. Прямая 2 является нагрузочной линией и описывается первым уравнением системы. Она отсекает на оси токов отрезок, численно равный току , а на оси напряжений – отрезок, численно равный напряжению .

Из семейства выходных характеристик необходимо выделить ту ВАХ, ток базы которой наиболее близок к полученной величине . Координаты точки пересечения – ток и напряжение 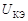– являются искомыми выходными током и напряжением рабочей точки транзистора.

При выполнении второго задания контрольной работы используем следующую методику.

Для определения 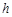-параметров достаточно иметь семейство входных и выходных статических характеристик БТ и координаты расчетной рабочей точки, которые должны быть одни и те же, как на графике с входными характеристиками, так и с выходными характеристиками.

Параметры 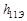и определяют по входным статическим характеристикам (рисунок 12 а). Для этого из определенной рабочей точки на линейной части характеристики проводят до пересечения с соседней характеристикой две прямые линии: одну – параллельно оси токов , другую параллельно оси напряжения . В полученном характеристическом треугольнике катет – приращение тока базы 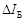, а катет – приращение напряжения базы 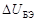. Приращение напряжения коллектора 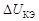– это разность напряжений, при которых снимались обе характеристики:

.

Из треугольника имеем

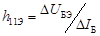при

и

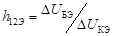при .

Параметры 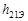и определяют по выходным статическим характеристикам (рисунок 12 б). Из рабочей точки проводят прямую, параллельно оси токов, до пересечения с соседней характеристикой, и определяют приращение тока коллектора (отрезок ) при 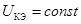. Приращение тока базы при этом составляет

,

отсюда

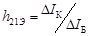при .

Чтобы определить параметр из рабочей точки проводят прямую линию, параллельную оси напряжений, на произвольное расстояние , равное 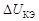, и определяют значение , равное отрезку . В результате

.

Рисунок 12 – Графическое определение 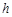-параметров

Задание 3

1 Перевести в десятичную систему счисления с точностью до трех знаков после запятой числа, указанные в таблице 4.

Таблица 4 – Исходные данные к заданию 3

Номер варианта	Основание СС	Номер варианта	Основание СС
P = 16	P = 2	P = 16	P = 2
	7C,A	110110,101		4B,C	101110,101
	D0,B	101101,011		A0,9	110010,011
	91,D	100110,010		8B,E6	111100,001
	BA,2	100011,110		E7,5	101010,010
	CA,F	111010,011		B9,C	100110,001

2 Перевести в двоичную систему счисления с точностью до трех знаков после запятой числа, указанные в таблице 5.

Таблица 5 – Исходные данные к заданию 3

Номер варианта	Основание СС	Номер варианта	Основание СС
P = 16	P = 10	P = 16	P = 10
	2F,AE	56,29		39,CA	48,32
	20,B6	73,19		5E,B9	31,62
	76,E5	67,27		07,A4	44,81
	0C,3E	47,36		D0,AB	42,72
	89,DC	96,82		0B,76	25,34

3 Перевести исходные числа (таблица 6) в двоичную систему счисления; выполнить алгебраическое сложение в прямом, обратном и дополнительных кодах, результат представить с точностью до четырех знаков после запятой в прямом коде.

Полученный результат перевести в десятичную систему счисления и сравнить с алгебраической суммой, вычисленной в десятичной системе счисления.

Таблица 6 – Исходные данные к заданию 3

Номер варианта	Десятичные числа	Номер варианта	Десятичные числа
	-17,15	+15,35		+25,85	-30,34
	-31,45	+26,14		+13,15	-14,95
	-18,16	+15,25		+13,76	-18,16
	-19,21	+16,14		+13,63	-17,81
	+11,25	-16,20		+12,42	-13,84

Методические указания по выполнению задания 3

Система счисления – совокупность символов (цифр) и приемов записи (изображения) чисел. Системы делятся на непозиционную (римскую) и позиционные (арабскую).

В позиционной системе счисления значение цифры определяется ее местом (позицией), изображающей число. Номер позиции, определяющий вес единицы на ней, называется разрядом. Основание системы счисления определяет количество используемых цифр или базу.

В общем случае целое число при использовании р -ичной системы можно записать в виде:

.

Наиболее широко применяемые системы:

10-я система: база – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

21₍₁₀₎=2^.10¹+1^.10⁰;

2-я система: база – 0, 1

21₍₁₀₎=1^.2⁴+0^.2³+1^.2²+0^.2¹+1^.2⁰=10101₍₂₎;

16-я система: база – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, А

21₍₁₀₎=1^.16¹+5^.16⁰=15₍₁₆₎.

Рассмотрим пример перевода шестнадцатеричного числа 5F,C83 в десятичную систему счисления:

.

Рассмотрим пример:

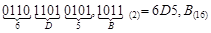
Наиболее простым способом перевода десятичного числа в двоичную систему счисления является следующий расчетный метод.

Целую часть числа последовательно делят на два до тех пор, пока целая часть частного от последовательного деления станет равна 0. Результат перевода состоит из цифр остатков, причем последний остаток будет представлять старший разряд в записи целой части двоичного числа.

Дробную часть переводят путем последовательного умножения на два. Результат перевода дробной части получают из цифр целых частей частичных произведений, причем старшим разрядом является первая целая часть.

Целая часть числа переводится точно, дробная – приблизительно. Точность перевода дробной части зависит от числа знаков после запятой.

При переводе целой части числа остатки, получающиеся в результате процесса последовательного деления, представляют цифры … целой части числа в новой системе счисления, записанные цифрами исходной СС. Последний остаток является старшей цифрой переведенного числа.

При переводе дробной части числа правильная дробь в новой системе записывается из целых частей произведений, получающихся при последовательном умножении, причем первая целая часть будет старшей цифрой новой дроби.

При переводе неправильных дробей отдельно преобразуется целая и дробная части, после чего записывается число в новой системе счисления.

Правила арифметики во всех позиционных системах аналогичны. Основной операцией является операция сложения. Вычитание легко сводится к сложению с применением специальных кодов для представления отрицательных чисел.

Обратный код отрицательного числа формируется по следующему правилу: в знаковом разряде сохраняется 1, а во всех остальных разрядах цифры меняются на обратные. Обратное преобразование из обратного кода в прямой производится по тому же правилу.

При использовании обратного кода операция вычитания реализуется как арифметическое сложение положительного числа, представленного в прямом коде, с отрицательным числом, представленным в обратном коде:

Перенос, возникающий из знакового разряда, при использовании обратного кода должен прибавляться в младший разряд суммы.

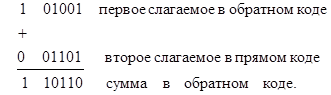
Результат сложения – отрицательное число и оно будет представлено в обратном коде.

Дополнительный код отрицательного числа образуется из обратного путем увеличения его на единицу младшего разряда. Для перехода от дополнительного кода отрицательного числа к прямому из исходного необходимо вычесть единицу младшего разряда, после чего во всех разрядах, за исключением знакового, заменить цифры на взаимно обратные.

При сложении складываются цифры знаковых разрядов с отбрасыванием возникающего из этого разряда переноса. Алгебраическая сумма является положительным числом и поэтому представлена в прямом коде.

Если сумма есть отрицательное число, оно оказывается представленным в дополнительном коде:

Основное достоинство обратного кода по сравнению с дополнительным состоит в простоте процесса его формирования. Однако скорость вычитания чисел в этом коде несколько ниже, чем в дополнительном.

Прямой, обратный и дополнительный коды положительных чисел совпадают (таблица 7).

Таблица 7 – Прямой, обратный и дополнительный коды положительных чисел

десят. СС	двоич. СС	прямой	обратный	дополнительный
+12(10)
-12(10)	-1100

Задание 4

Разработать логическую схему КЦУ, функционирование которого задано таблицей истинности (таблица 7).

1 Записать СДНФ и СКНФ.

2 Построить логическую схему устройства в базисе И, ИЛИ, НЕ.

3 Записать СДНФ через логическую операцию И-НЕ.

4 Построить логическую схему устройства в базисе И-НЕ.

5 Записать СКНФ через логическую операцию ИЛИ-НЕ.

6 Построить логическую схему устройства в базисе ИЛИ-НЕ.

7 Проверить правильность функционирования логических схем КЦУ для пятого набора аргументов.

8 Выполнить расчет затрат оборудования по Квайну, сделать вывод.

Таблица 7 – Исходные данные к заданию 4

Номер набора аргументов

Наборы аргументов

Номер варианта

х 3

х 2

х 1

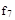
Методические указания по выполнению задания 4

Все схемы цифровых устройств построены на элементах, выполняющих логические операции. Такие элементы принято называть логическими элементами (ЛЭ). При конкретной физической реализации логических состояний используются элементы, для которых характерны два устойчивых состояния. Например, электрическое реле – замкнуто, разомкнуто; элемент индикации – светится, не светится и т.д.

В логике не требуется знания абсолютного значения величины, поэтому физическая величина, подвергаемая логическим преобразованиям, называется переменной, или аргументом, и представляется как более положительная (Н) или менее положительная (L). Этим двум значениям, называемым логическими уровнями, условно присваиваются значения лог. 1 и лог. 0, или, наоборот, в зависимости от принятого соглашения.

Логические переменные могут подвергаться различным преобразованиям с использованием логических элементов (ЛЭ). Такие преобразования описываются с помощью переключательных (логических) функций. Функция от входных переменных называется переключательной (логической), если она так же, как ее аргументы, принимает два значения: лог. 1 или лог. 0. На рисунке 13 представлен условный логический элемент, реализующий определенную функцию в зависимости от значений входных переменных.

Рисунок 13 – Условное графическое обозначение (УГО) ЛЭ

Любая логическая функция (ЛФ) может быть задана двумя способами: в виде формул и в виде таблиц истинности (ТИ). В ТИ приводятся значения ЛФ в зависимости от сочетания переменных.

При этом для того чтобы задать переключательную функцию, не обязательно задавать все ее значения при всех сочетаниях переменных, а достаточно знать состояния, при которых она, например, равна лог. 1, так как для всех остальных состояний переменных значение ЛФ равно лог. 0.

В формульном виде функция в своей основе имеет набор логических произведений (или сумм) переменных, связанных между собой, как правило, знаками логических сумм (или произведений).

Произведение переменных, в которое каждая из переменных входит только один раз в прямом или инверсном виде, называется минтермом (т).

Сумма переменных, в которую каждая из переменных входит только один раз в прямом или инверсном виде, называется макстермом (М).

Так, например, у двух переменных может бытьчетыре возможных макстерма или минтерма, виды которых представлены в таблице 4.

Таблица 8 – Макстеры и минтермы двух переменных

Переменные	Макстермы	Минтермы
х 2	х 1	М	т

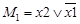
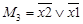
Количество переменных, входящих в макстерм или минтерм, называется рангом. В рассматриваемом примере ранг равен 2.

Рассмотрим правила перехода от табличной формы записи ЛФ к формульной. Например, функция задана в виде таблицы истинности (таблица 9).

Таблица 9 – Таблица истинности ЛФ

М	х 3	х 2	х 1	f	т

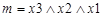
Для перехода от табличной формы к формульной следует руководствоваться следующими положениями.

1. Если функция алгебры логики задана таблицей истинности, то из таблицы всегда можно взять логическую сумму – дизъюнкцию всех переменных, для которых ЛФ равна единице. Эта запись будет точно представлять функцию и называться совершенной дизъюнктивной нормальной формой (СДНФ) представления функции. СДНФ – это логическая сумма минтермов, при которых значение функции равно единице:

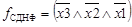
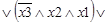
. (1)

2. Если функция алгебры логики задана таблицей истинности, то из таблицы всегда можно взять логическое произведение – конъюнкцию всех переменных, для которых ЛФ равна нулю. Эта запись будет точно представлять функцию и называться совершенной конъюнктивной нормальной формой (СКНФ) представления функции. СКНФ – это логическое произведение макстермов, при которых значение функции равно нулю:

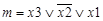
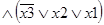
. (2)

Одна из основных задач синтеза ЦУ заключается в выборе типов элементов, на которых будут реализовываться заданные функции. Поэтому необходимо определить минимальный набор логических элементов (базис), образующих функционально полную систему элементов.

Базис – это функционально полный набор элементов, с помощью которого можно реализовать сколь угодно сложную переключательную функцию. Их может быть несколько. Базис из логических элементов И, ИЛИ, НЕ (рисунок 14) называют основным.

Рисунок 14 – Условное графическое обозначение ЛЭ И, ИЛИ, НЕ

Также функционально полную систему образуют логический элемент И-НЕ или ИЛИ-НЕ (рисунок15).

Рисунок 15 – Условное графическое обозначение ЛЭ И-НЕ, ИЛИ-НЕ

В таблице 10 представлены отечественные и зарубежные аналоги условных графических обозначений основных логических элементов, которые реализуют ЛФ двух аргументов.

Таблица 10 – Зарубежные аналоги УГО ЛЭ

Логическая функция	Отечественное УГО	Зарубежное УГО
НЕ
И
ИЛИ
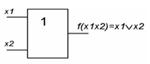
И-НЕ
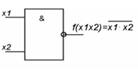
ИЛИ-НЕ

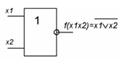
Требования к построению схем цифровых устройств изложены в соответствующих стандартах. Схема цифрового устройства представляет собой совокупность условных графических обозначений микросхем, на которых реализовано это устройство, и связей между ними.

Построим логическую схему устройства по выражению (1). Для этого потребуется:

1 пять логических элементов 2 И;

2 один логический элемент 5 ИЛИ;

3 три логических элемента НЕ.

Логическая схема устройства в базисе И, ИЛИ, НЕ, построенная по логической функции (1), представлена на рисунке 16.

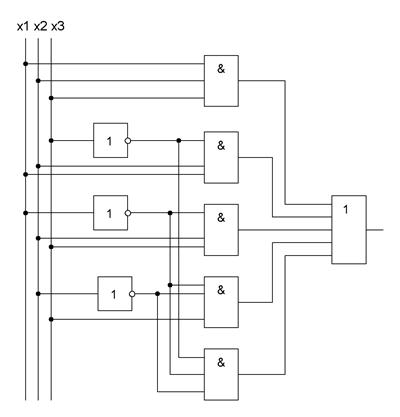
Рисунок 16 – Логическая схема устройства в базисе И, ИЛИ, НЕ

Проверим правильность функционирования логической схемы КЦУ. Для этого проставим на выходах всех логических элементов значения сигналов для пятого набора аргументов, полученный на выходе сигнал сравним со значением функции в таблице истинности.

Построим логическую схему устройства по выражению (2). Для этого потребуется:

1 два логических элемента 2 И;

2 один логический элемент 3 ИЛИ;

3 три логических элемента НЕ.

Логическая схема устройства в базисе И, ИЛИ, НЕ, построенная по логической функции (2), представлена на рисунке 17.

Рисунок 17 – Логическая схема устройства в базисе И, ИЛИ, НЕ

Проверим правильность функционирования логической схемы КЦУ. Для этого проставим на выходах всех логических элементов значения сигналов для пятого набора аргументов, полученный на выходе сигнал сравним со значением функции в таблице истинности.

Рассмотрим пример синтеза КЦУ в базисе И-НЕ для той же ЛФ.

Преобразуем ЛФ (1) в базис И-НЕ, используя правило де Моргана и закон двойного отрицания:

=

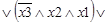
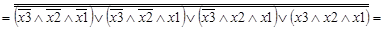
Построим логическую схему устройства в базисе И-НЕ по выражению (1), при этом одиночные отрицания аргументов реализуем на основе ЛЭ 2 И-НЕ с объединенными входами. Для этого необходимо использовать:

1 три логических элемента 2 И-НЕ;

2 пять логических элементов 3 И-НЕ.

3 один логический элемент 5 И-НЕ.

Логическая схема устройства в базисе И-НЕ представлена на рисунке 18.

Рисунок 18 – Логическая схема устройства в базисе И-НЕ

Проверим правильность функционирования логической схемы КЦУ. Для этого проставим на выходах всех логических элементов значения сигналов для пятого набора аргументов, полученный на выходе сигнал сравним со значением функции в таблице истинности.

Преобразуем ЛФ (2) в базис ИЛИ-НЕ, используя правило де Моргана и закон двойного отрицания:

.

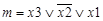
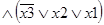
Построим логическую схему устройства в базисе ИЛИ-НЕ по выражению (2), при этом одиночные отрицания аргументов реализуем на основе ЛЭ 2 ИЛИ-НЕ с объединенными входами. Для этого необходимо использовать:

1 три логических элемента 2 ИЛИ-НЕ;

2 четыре логических элемента 3 ИЛИ-НЕ.

Логическая схема устройства в базисе ИЛИ-НЕ представлена на рисунке 19.

Рисунок 19 – Логическая схема устройства в базисе ИЛИ-НЕ

Проверим правильность функционирования логической схемы КЦУ.

Для этого проставим на выходах всех логических элементов значения сигналов для пятого набора аргументов, полученный на выходе сигнал сравним со значением функции в таблице истинности.

Выполним расчет затрат оборудования по Квайну (С) для логических схем КЦУ (рисунки 16-19).

Так как количество входов у всех логических элементов КЦУ является объективной мерой для оценки сложности КЦУ и каждому входу ЛЭ соответствует технический компонент (условный транзистор), то затраты оборудования по Квайну для схем соответственно равны:

С=5х2+1х5+3х1=18 (усл. транзисторов);

С=2х2+1х3+3х1=10 (усл. транзисторов);

С=3х2+5х3+1х5=26 (усл. транзисторов);

С=3х2+4х3=18 (усл. транзисторов).

По полученным результатам можно сделать вывод, что схема, построенная по СКНФ в основном базисе, является более экономичной. При этом следует помнить, что данная оценка объективна, доступна разработчику на самых ранних этапах проектирования, но при этом не является абсолютной, и поэтому при синтезе КЦУ используется ряд других критериев.

Задание 5

Дать письменный ответ на вопрос, номер которого определяется по таблице 11.

Номер вопроса выбирается согласно вариантам контрольной работы (таблица 11) – предпоследняя цифра номера студенческого билета обозначена буквой , а последняя цифра – буквой .

Таблица 11 – Номера вопросов для задания № 5 согласно вариантам контрольной работы

ху

Перечень вопросов для выполнения задания № 5

1. Шифраторы: определение, назначение, условное графическое обозначение, пример синтеза, пример микросхемы.

2. Дешифраторы: определение, назначение, условное графическое обозначение, пример синтеза, пример микросхемы.

3. Мультиплексоры: определение, назначение, условное графическое обозначение, пример синтеза, пример микросхемы.

4. Демультиплексоры: определение, назначение, условное графическое обозначение, пример синтеза, пример микросхемы.

5. Двоичные сумматоры: определение, назначение, условное графическое обозначение, пример синтеза, пример микросхемы.

6. Асинхронный RS-триггер с прямыми входами: условное графическое обозначение, таблица состояний, схемотехническая реализация и принцип работы, пример микросхемы.

7. Асинхронный RS-триггер с инверсными входами: условное графическое обозначение, таблица состояний, схемотехническая реализация и принцип работы, пример микросхемы.

8. Синхронные RS-триггер: условное графическое обозначение, таблица состояний, схемотехническая реализация и принцип работы, пример микросхемы.

9. D со статическим управлением: условное графическое обозначение, таблица состояний, схемотехническая реализация и принцип работы, пример микросхемы.

10. JK-триггеры со статическим управлением: условное графическое обозначение, таблица состояний, схемотехническая реализация и принцип работы, пример микросхемы.

ПРИЛОЖЕНИЕ А

Диодные схемы для расчета задания № 1

Рисунок А.1 – Диодная схема 1 для расчета задания № 1

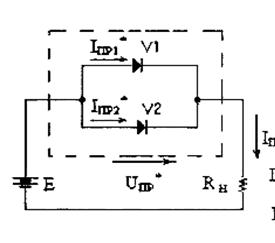
Рисунок А.2 – Диодная схема 2 для расчета задания № 1

Рисунок А.3 – Диодная схема 3 для расчета задания № 1

ПРИЛОЖЕНИЕ Б

Рисунок Б.1 – Вольт-амперная характеристика

Германиевого диода Д312А

ПРИЛОЖЕНИЕ В

Дата добавления: 2014-11-25