Теорема Котєльнікова

Аналогічні результати отримані і при використанні теореми Котєльнікова [7, 8]: довільний сигнал, спектр якого не має частот вище f_m (Гц), може бути повністю відтворений, якщо відомі значення цього сигналу, взяті через рівні проміжки часу r_t =1/(2´ f_m) (c).

У відповідності з цією теоремою сигнал s(t) обмежений за спектром найвищою частотою W_m=2× p ×F_m, можна представити рядом:

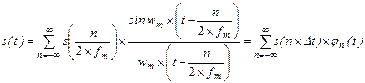(2.4)

В цьому виразі 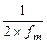= 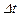означає інтервал між двома відліками на осі часу, а 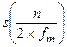= 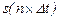- вибірки функції s(t) в момент часу t= .

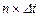Представлення заданої функції s(t) рядом (2.4) ілюструється рисунком 2.2.

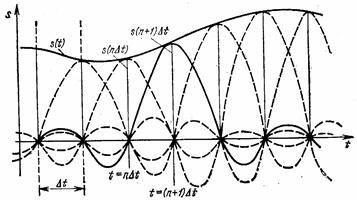Рисунок 2.2 - Представлення сигналу рядом Котєльнікова

Функція виду

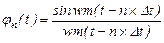(2.5)

має наступні властивості:

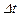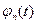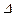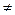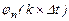1) в точці t=n× × =1, а в точках t=k× t, де k – будь-яке ціле додатне або від’ємне число, яке не дорівнює n (k n), =0

2) Спектральна густина функції 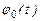рівномірна в полосі частот і рівна .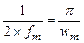

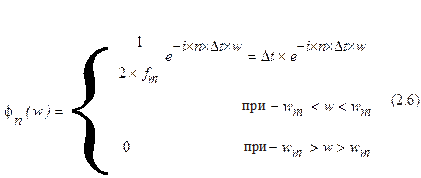
Так як функція 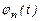відрізняється від 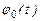тільки зсувом по осі часу на величину 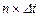, то спектральна густина функції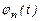

Те, що ряд (2.4) точно визначає заданий сигнал s(t) в точках відліку, не потребує додаткового доведення, оскільки коефіцієнтами ряду є самі виборки із функції, тобто величини s(n´Δt). Можна довести, що ряд (2.4) визначає функцію s(t) в будь-який момент t, а не тільки в точках відліку t=n´Δt.

Розкладемо сигнал по функціях виду (2.5) для яких інтервал ортогональності рівний нескінченності, а норма:

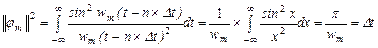(2.7)

Не визначаючи наперед значення коефіцієнтів ряду (2.4) застосовуємо для їх визначення загальну формулу, справедливу для узагальненого ряду Фур’є:

С_n= 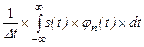(2.8)

При цьому ми виходимо з умови, що s(t) – квадратично інтегрована функція (енергія сигналу скінчена).

Для обчислення інтегралу у виразі (2.8) скористаємося формулою:

(2.9)

Межі інтегрування тут приведені у відповідності із заданою граничною частотою 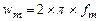у спектрі сигналу, а також у спектрі функції .

Інтеграл у правій частині (2.9) з коефіцієнтом 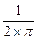є не що інше, як значення s(t) в момент 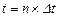. Таким чином,

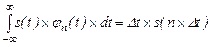(2.10)

Підставляючи цей результат у (2.8) отримуємо кінцевий вираз:

С_n= 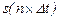(2.11)

Із якого слідує, що коефіцієнтами ряду (2.4) є вибірки функції s(t) в точках t= .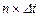

Оскільки обмеження спектру кінцевою найвищою частотою забезпечує неперервність функції s(t), ряд (2.4) сходиться до функції s(t) при любому значенні t.

Якщо взяти інтервал між вибірками 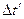меншим ніж 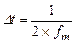, то ширина 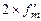спектру 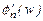функції 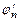буде більша ніж у спектру s(w) сигналу s(t) (рис.2.3), але це не відіб’ється на величині коефіцієнта C_{n .}

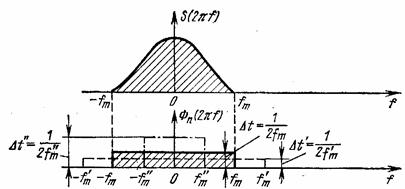Рисунок 2.3 - Зв’язок між спектром сигналу s(t) і спектром базисної функції φ_n(t)

Модуль функції 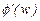зображений на рис.2.3 штриховою лінією.

При збільшенні 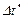в порівнянні з 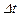спектр 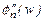функції 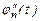(на рис. 2.3 показаний штрих-пунктиром) стає вужчим ніж спектр сигналу s(t), і при обчисленні інтегралу у виразі (2.9) межі інтегрування повинні бути 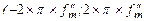) замість 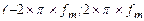). Коефіцієнти С_n при цьому є уже виборками не заданого сигналу s(t), а деякої іншої функції s₁(t), спектр якої обмежений найвищою частотою .

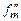І так, зменшення інтервалів між вибірками в порівнянні з величиною 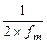допустимо, але не має змісту. Збільшення ж інтервалу понад величину 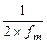недопустимо.

2.1.3 Стискання цифрових даних акустичного каротажу при передачі по каротажному кабелі

При створенні комплексу модульних приладів для каротажа свердловин які буряться, необхідно враховувати і раціонально використовувати інформаційні можливості цифрових систем передачі даних по каротажному кабелі [9]. Найпоширеніші системи передачі цифрових даних типу “КАРАТ” (Тверьгеофизика) і “Сибирь-НВ” (Геоприм, м.Краснодар) базуються на протоколі цифрового каналу передачі даних кодами типу “Манчестер-2” (стандарт США MIL-STD-1553B) і забезпечують максимальну швидкість передачі даних 20 і 100 Кбіт/с відповідно.

Розрахунки показують, що для комплексної апаратури, яка включає скануючі методи електричного каротажу високої роздільної здатності, багатозондового електромагнітного каротажу і багатоелементного хвильового акустичного каротажу, можливості типового цифрового каналу передачі даних будуть обмежувати швидкість каротажу. Істотний вклад в цю проблему вносить потік даних багатоелементного зонда АК.

Так, наприклад, восьмиелементний зонд АК з часом дискретизації сигналів АК Δt = 2 мкс, тривалістю перетворення сигналу (траси) 4000 мкс і 16-розрядним АЦП забезпечує завантаження каналу передачі потоком даних 32000 біт на кожну точку глибини, що при кроці квантування за глибиною 10 см і швидкості каротажу 30 см/с (~1200 м/год) буде вимагати повного завантаження цифрового каналу зі швидкістю 200кбіт/с (час на передачу 16-розрядного слова разом зі службовими бітами для каналу 200кбіт/с складає 100мкс).

Аналогічна проблема може виникнути в автономних комплексах каротажної апаратури на трубах, де на перший план виходить раціональне використання об’ємів флеш-пам’яті і економія енергії акумуляторів для збільшення часу автономної роботи системи.

Для зменшення потоку цифрових даних хвильового АК запропонований і випробуваний метод стискання початкової інформації і наступного її відтворення – “метод характерних точок АК”.

“Метод характерних точок” може застосовуватись як у варіанті обробки вже зформованого потоку цифрових даних АК у свердловинному приладі, так і у варіанті керування в реальному масштабі часу затримками запуску аналого-цифрового перетворення вхідних сигналів АК. Розглянемо перший варіант – робота з початковим потоком цифрових даних АК.

Дата добавления: 2014-11-25