Гранные поверхности и многогранники

Образование и классификация поверхностей

Охрана животных

Охрана лесов

· Повышение продуктивности лесов (лесопосадки).

· Защита от пожаров и вредителей.

· Охрана ценных и редких видов растений (состоит в рациональном, нормированном сборе, исключающем их истощение).

Для сохранения редких и исчезающих видов организуют заповедники, заказники, животных расселяют в районы их былого распространения, подкармливают, создают укрытия и искусственные гнездовья, охраняют от хищников и болезней. При очень низкой численности животных разводят в неволе (питомниках и зоопарках), а затем выпускают в подходящие для них природные условия.

Система охраны диких животных складывается из мер:

· по охране самих животных от прямого истребления, гибели от стихийных бедствий;

· по сохранению их среды обитания.

Охрана самих животных осуществляется законами об охоте: запрет охоты на редкие виды, ограничение сроков, норм, мест и способов добычи других промысловых видов.

Иванищук Петр Петрович

Куликова Надежда Анатольевна

БИОЛОГИЯ

Лекции для иностранных студентов

Редактор А.М. Панкова

Лицензия № 00637 от 05.01.2000 г.

______________________________________________________________________________________________

Подписано в печать 2005 г. Формат 60 × 84 ¹/₁₆.

Уч.-изд. л. 11,2.

Тираж 100 экз. Заказ

______________________________________________________

Ивановская государственная медицинская академия.

153012, г. Иваново, пр. Ф. Энгельса, 8.

Типография ГОУ СПО ИЭК, 153025, г. Иваново, ул. Ермака, 41.

Поверхностью называют множество последовательных положений линии, перемещающейся в пространстве. Эта линия может быть прямой или кривой и называется образующей поверхности.

Линия, с помощью которой задается направление перемещения образующей, называется направляющей.

Любую поверхность можно получить разными способами.

Например, прямой круговой цилиндр можно создать вращением образующей l вокруг оси I параллельной ей. А можно - перемещением окружности m, центр которой скользит по оси.

Также любая кривая k, лежащая на поверхности цилиндра, образует эту поверхность при своем вращении вокруг оси (рис. 5.1.1).

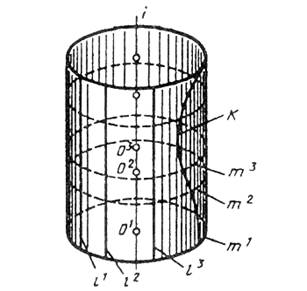
Рисунок 5.1.1

На практике из всех возможных способов образования поверхности выбирают наиболее простой.

В зависимости от формы образующей все поверхности можно разделитьна:

· линейчатые – образующая прямая линия (рис. 5.1.2.а);

· нелинейчатые(криволинейные) – образующая кривая линия (рис. 5.2.б).

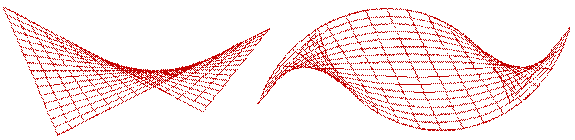
а б

Рисунок 5.1.2

В линейчатых поверхностях выделяют поверхности развертывающиеся, совмещаемые всеми своими точками с плоскостью без разрывов и складок, и неразвертывающиеся, которые нельзя совместить с плоскостью без разрывов и складок.

К развертывающимся поверхностям относятся:

· гранные;

· конические;

· цилиндрические;

· торсовые поверхности.

Все остальные поверхности — неразвертывающиеся.

Гранные поверхности образуются перемещением прямолинейной образующей по ломанной направляющей. При этом, если одна точка образующей (S) неподвижна, создается пирамидальная поверхность (рис. 5.2.1.а). Если образующая параллельна заданному направлению, то создается призматическая поверхность (рис.5.2.1.б).

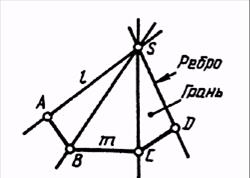
а б

Рисунок 5.2.1

Замкнутые гранные поверхности называются многогранниками. Элементами многогранников являются:

· вершина – точка S образующей (у призмы она находится в бесконечности);

· грань - часть плоскости, ограниченная направляющей и образующими;

· ребро – линия пересечения соседних граней;

· основание – часть плоскости, ограниченная направляющей.

Многогранник называется выпуклым, если весь он лежит по одну сторону от плоскости любой его грани. Из всего многообразия выпуклых многогранников наибольший практический интерес представляют: пирамиды, призмы, призматоиды.

Пирамида это многогранник, в основании которого лежит произвольный многоугольник, а боковые грани — треугольники с общей вершиной S (5.2.2.а).

а б

Рисунок 5.2.2

Призма — многогранник, у которого основания это два одинаковых и взаимно параллельных многоугольника, а боковые грани — параллелограммы (рис. 5.2.2.б).

На комплексном чертеже многогранники задают проекциями их вершин и ребер с учетом видимости. Видимость ребер определяют с помощью конкурирующих точек.

Любую точку на гранной поверхности можно построить с помощью образующей, проходящей через эту точку.

На рис. 5.2.3. приведен пример построения на комплексном чертёже пирамиды ABCD точки М, принадлежащей грани ABC. Если по условию задачи известна фронтальная проекция точки М2, то через нее на плоскости A2B2C2 проводится прямая С252, а затем с помощью линий связи находится горизонтальная проекция С151. Горизонтальная проекция точки М находится на С151 и определяется с помощью линии связи, проведенной из М2.

Рисунок 5.2.3

На рис. 5.2.4 дан комплексный чертеж прямой четырехугольной призмы с горизонтально проецирующей поверхностью.

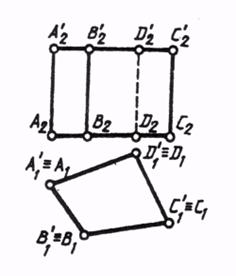
Рисунок 5.2.4

Если ребра призмы перпендикулярны плоскостиоснования, такую призму называют прямой. Если у призмы ребра перпендикулярны какой-либо плоскости проекций, то боковую поверхность ее называют проецирующей.

ЛЕКЦИЯ №5: Поверхности (продолжение).

Дата добавления: 2014-11-25