Из этого следует, что при равновероятности знаков алфовита энтропия определяется исключительно числом знаков m алфавита и по существу является характеристикой только алфавита

Свойства энтропии

В дальнейшем в выражениях для количества информации I и энтропии H всегда используют логарифмы с основанием 2.

При равновероятности знаков алфавита Рi = 1/m из формулы Шеннона получают:

.

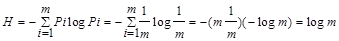Если же знаки алфавита неравновероятны, то алфавит можно рассматривать как дискретную случайную величину, заданную статистическим распределением частот n_i появления знаков х_i (или вероятностей Рi =n_i / n) табл. 2.1:

Таблица 2.1.

Знаки хi	x1	x2	...	xm
Частоты ni	n1	n2	...	nm

Такие распределения получают обычно на основе статистического анализа конкретных типов сообщений (например, русских или английских текстов и т.п.).

Поэтому, если знаки алфавита неравновероятны и хотя формально в выражение для энтропии входят только характеристики алфавита (вероятности появления его знаков), энтропия отражает статистические свойства некоторой совокупности сообщений.

На основании выражения

,

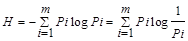
величину log 1/Pi можно рассматривать как частную энтропию, характеризующую информативность знака х_i, а энтропию H - как среднее значение частных энтропий.

Функция (Pi × log Pi) отражает вклад знака х_i в энтропию H. При вероятности появления знака Pi=1 эта функция равна нулю, затем возрастает до своего максимума, а при дальнейшем уменьшении Pi стремится к нулю (функция имеет экстремум): рис.2.1.

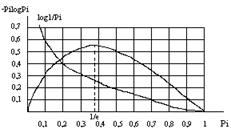
Рис. 2.1. Графики функций log 1/Pi и -Pi × log Pi

Для определения координат максимума этой функции нужно найти производную и приравнять ее к нулю.

Из условия 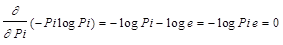находят: Pi e = 1,где е - основание натурального логарифма.

Таким образом, функция: (Pi log Pi) при Pi = 1/e = 0,37 имеет максимум: 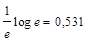., т.е координаты максимума (0,37; 0,531)

Энтропия Н - величина вещественная, неотрицательная и ограниченная, т.е. Н ³ 0 (это свойство следует из того, что такими же качествами обладают все ее слагаемые Pi log 1/Pi).

Энтропия равна нулю, если сообщение известно заранее (в этом случае каждый элемент сообщения замещается некоторым знаком с вероятностью, равной единице, а вероятности остальных знаков равны нулю).

Энтропия максимальна, если все знаки алфавита равновероятны, т.е. Н_max = log m.

Таким образом, степень неопределенности источника информации зависит не только от числа состояний, но и от вероятностей этих состояний. При неравновероятных состояниях свобода выбора источника ограничивается, что должно приводить к уменьшению неопределенности. Если источник информации имеет, например, два возможных состояния с вероятностями 0,99 и 0,01, то неопределенность выбора у него значительно меньше, чем у источника, имеющего два равновероятных состояния. Действительно, в первом случае результат практически предрешен (реализация состояния, вероятность которого равна 0,99), а во втором случае неопределенность максимальна, поскольку никакого обоснованного предположения о результате выбора сделать нельзя. Ясно также, что весьма малое изменение вероятностей состояний вызывает соответственно незначительное изменение неопределенности выбора.

Пример3. Распределение знаков алфавита имеет вид р(х₁) = 0,1 р(x₂) = 0,1 р(x₃) = 0,1 р(x₄) = 0,7. Определить число знаков другого алфавита, у которого все знаки равновероятны, а энтропия такая же как и у заданного алфавита.

Особый интерес представляют бинарные сообщения, использующие алфавит из двух знаков: (0,1). При m = 2 сумма вероятностей знаков алфавита: Р₁₊Р₂ = 1. Можно положить Р₁ = Р, тогда Р₂ = 1-Р.

Энтропию можно определить по формуле:

,

Энтропия бинарных сообщений достигает максимального значения, равного 1 биту, когда знаки алфавита сообщений равновероятны, т.е. при Р = 0,5, и ее график симметричен относительно этого значения.(рис.2.2).

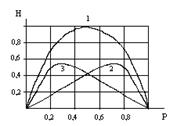
Рис. 2.2. График зависимости энтропии Н двоичных сообщений (1) и ее составляющих (2,3): - (1 - Р) log (1 - P) и - P log P от Р.

Пример 4. Сравнить неопределенность, приходящуюся на букву источника информации (алфавита русского языка), характеризуемого ансамблем, представленным в таблице 2.2, с неопределенностью, которая была бы у того же источника при равновероятном использовании букв.

Таблица 2.2.

Буква	Вероятность	Буква	Вероятность	Буква	Вероятность	Буква	Вероятность
а	0,064	й	0,010	т	0,056	ы	0,016
б	0,015	к	0,029	у	0,021	э	0,003
в	0,039	л	0,036	ф	0,02	ю	0,007
г	0,014	м	0,026	х	0,09	я	0,019
д	0,026	н	0,056	ц	0,04	пробел	0,143
е,ё	0,074	о	0,096	ч	0,013
ж	0,008	п	0,024	ш	0,006
з	0,015	р	0,041	ш	0,003
и	0,064	с	0,047	ъ,ь	0,015

Решение. 1. При одинаковых вероятностях появления любой из всех m = 32 букв алфавита неопределенность, приходящуюся на одну букву, характеризует энтропия

H = log m = log 32 = 5 бит.

2. Энтропию источника, характеризуемого заданным табл. 2.2 ансамблем, находят по формуле:

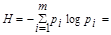-0,064 log 0,064 -0,015log0,015 - 0,143log0,143» 4,43 бит.

Таким образом, неравномерность распределения вероятностей использования букв снижает энтропию источника с 5 до 4,42 бит

Пример 5. Заданы ансамбли Х и Y двух дискретных величин:

Таблица 2.3.

Случайные величины хi	0,5	0,7	0,9	0,3
Вероятности их появления	0,25	0,25	0,25	0,25

Таблица 2.4.

Случайные величины уj
Вероятности их появления	0,25	0,25	0,25	0,25

Сравнить их энтропии.

Решение. Энтропия не зависит от конкретных значений случайной величины. Так как вероятности их появления в обоих случаях одинаковы, то

Н(Х) = Н(Y) = - 4(0,25log0,25) = -4(1/4log1/4) =

= log 4 = 2 бит

Дата добавления: 2014-11-25