Теоретичні відомості. Порядок виконання роботи

МАКСВЕЛЛІВСЬКИЙ РОЗПОДІЛ МОЛЕКУЛ ГАЗУ ЗА ШВИДКОСТЯМИ

Лабораторна робота № 191

Порядок виконання роботи

1. Промити бюретку дистильованою водою (2 - 3 см³).

2. Налити у бюретку 15...20 см³ дистильованої води, підставити під бюретку хімічний стакан і відрегулювати швидкість витікання води так, щоб можна було рахувати краплі.

3. Обчислити число крапель в одному і тому ж об'ємі рідини, що витікає. Для вимірювання досить 2 см³. Вимірювання повторити 5 разів, їх результати записати у таблицю та обчислити середнє значення числа крапель у взятому об’ємі рідин.

4. Після вимірювань воду злити у посудину з дистильованою водою.

5. Налити у бюретку досліджувану рідину об'ємом 15...20см³ і виміряти число крапель у тому ж об'ємі рідини (2 см³). Вимірювання повторити 5 разів,

дані вимірювань записати у таблицю та обчислити середнє значення числа крапель у взятому об’ємі рідин.

6. Взяти з таблиці (див. ДОДАТОК І) значення σ_е і ρ_е при кімнатній температурі. За середнім значенням числа крапель обчислити коефіцієнт поверхневого натягу досліджуваної рідини за формулою (190.3).

Таблиця 190.1

Величина	Речовина
Дистильована вода	Досліджувана рідина
Число крапель, n
Середнє значення числа крапель
Густина ρ, кг/м^3
Коефіцієнт поверхневого натягу σ, Н/м

7. Зробити висновок.

Контрольні запитання

1. Яка величина називається коефіцієнтом поверхневого натягу?

2. Чому при відсутності зовнішніх сил крапля рідини набуває сферичної форми?

3. Від чого залежить коефіцієнт поверхневого натягу?

4. За яких умов відбувається відрив краплі від капіляра?

Мета роботи - ознайомитись з методикою обчислень та побудовою функції Максвелла для розподілу молекул за швидкостями. Визначити частку молекул, швидкості яких лежать в заданому інтервалі швидкостей.

Прилади і матеріали: аркуш міліметрового паперу розміром 200×200 мм, таблиці зі значеннями залежності функції розподілу за швидкостями при заданій температурі.

У довільному макроскопічному об’ємі молекули газу рухаються з різними швидкостями (від 0 до ∞ м/с). Оскільки молекули мають скінченні розміри і безперервно стикаються одна з одною (за нормальних умов молекула робить 10⁹ зіткнень за 1 с), неможливо підрахувати число молекул, які мають задане значення швидкості. Але можна обчислити число молекул, швидкості яких лежать в інтервалі від Jдо J + d J.

Вперше Максвелл теоретично розв’язав задачу про розподіл молекул ідеального газу за швидкостями. Вчений розглядав газ як сукупність великої кількості однакових молекул в умовах термодинамічної рівноваги (р, V, Т постійні) за відсутності зовнішнього силового поля. Функцію розподілу молекул газу за швидкостями Максвелл одержав за допомогою методів теорії ймовірностей. Вона має вигляд:

F_M = 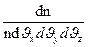= (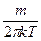)^3/2 e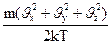^- (191.1)

Ця функція визначає ймовірне число молекул массою m, які при заданій температурі Т мають проекції швидкості на осі координат, що лежать в інтервалі від J_хдо J_х + dJ_х; J_yдо J_y + dJ_y; J_zдо J_z + dJ_z.

Тоді число молекул dn, абсолютне значення швидкостей яких лежить в інтервалі від J до J + d Jвизначають за формулою

d n = n (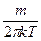)^3/2 e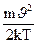^- 4pJ²dJ (191.2)

Оскільки

dJ_х dJ_y dJ_z = 4pJ² dJ; m = ; R = kN_A

де μ- молярна маса; N_A - число Авогадро; R – універсальнагазова стала; k – стала Больцмана; m – масса однієї молекули, то рівняння (191.1) запишемо у вигляді:

F_M = = (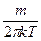)^3/2 e^- 4pJ² (191.2)

З цієї формули видно, що конкретний вид функції залежить від природи газу (від його молярної маси) та від параметра його стану (температури).

Із статистичного розподілу молекул за швидкостями були встановлені наступні висновки:

1) Який би не був розподіл молекул за швидкостями, в термодинамічно рівноважній системі завжди встановлюється розподіл Максвелла.

2) Якщо в системі вже встановився розподіл Максвелла, то він буде існувати нескінченно довго.

Максимум функції розподілу досягається при найбільш ймовірній швидкості руху молекул. Для визначення значення ймовірної швидкості треба використати умову для максимуму виразу F_M, формули (191.2) тобто

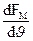= 4p (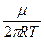)^3/2 2J(1- ) = 0

звідки J_йм = 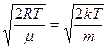(191.3)

Крім найбільш ймовірної швидкості, з функції розподілу можна обчислити середню арифметичну швидкість поступального руху молекул:

= = ,

та середню квадратичну швидкість молекул: _кв == =

На рис. 191.1 наведено криві закону розподілу молекул за швидкостями при Т₁ та Т₂. Частина молекул dn газу, швидкості яких лежать в інтервалі від J до J + dJ чисельно дорівнює площі dS криволінійної трапеції (заштрихована ділянка на рис. 191.1). Вся площа, обмежена кривою розподілу і віссю абсцис, чисельно дорівнює числу молекул, швидкості яких мають різні значення від 0 до ∞.

Якщо ввести відносну швидкість руху молекул u, то функція Максвелла матиме вигляд:

F_M = 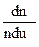= e^- u² (191.4)

Відносне число молекул, швидкості яких мають значення від 0 до u_i, буде:

= (191.5)

Обчислення інтегралу (191.5) за частинами дає наступну формулу:

(191.6)

Інтеграл в (191.6) є інтегралом ймовірності, значення якого наведені у ДОДАТКУ ІІ до лабораторної роботи для значень верхньої межі інтегрування u_i.

Порядок виконання роботи

1. На міліметрівці за наданими в таблиці значеннями F_M = f (J)побудувати на одних і тих же осях координат дві криві розподілу молекул.

Масштаб: для J; 1мм - 10 м/с; для F_M = 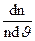відповідно 10 мм - 1·10^-3.

2. За формулою обчислити для двох температур ймовірну швидкість і визначити її значення графічно за положенням максимуму на кривих розподілу. Зробити висновок.

3. Визначити відносне число молекул , які мають швидкість в інтервалі від J₁ = 200 м/с до J₂ =300 м/с для заданої температури. Для цього необхідно:

а) визначити площу S₀, що лежить під кривою розподілу для заданої температури.

б) визначити площу S₁, обмежену швидкостями J₁і J₂та кривою розподілу при Т₁.

в) відношення S₁ до S₀ визначає відносне число молекул, швидкості яких лежать в межах від J₁до J₂ при Т₁.

г) повторити пункти б), в) для температури Т₂.

4. Обчислити відносні швидкості u₁ і u₂ як відношення швидкостей

J₁ = 200 м/с і J₂ = 300 м/с до ймовірної швидкості при даній температурі.

5. За формулою (191.6) підрахувати відносне число молекул зі швидкостями від 0 до u₁ і від 0 до u₂. Різниця між цими величинами і дає значення відносного числа молекул зі швидкостями від u₁ до u₂ тобто від J₁ до J₂:

= -

6. Порівняти результати обчислень в пунктах 3 і 5 і зробити висновки.

Дата добавления: 2014-11-25