Тема 6. Выборочное наблюдение

Выборочным называется несплошное наблюдение, при котором обследованию и изучению подвергается не вся исходная совокупность, а специально отобранная ее часть.

Средняя (стандартная) ошибка выборки (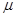) характеризует среднюю величину возможных расхождений средней выборочной величины (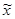) и генеральной средней (), т. е. справедливо соотношение .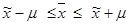

Предельная ошибка выборки ( 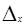) рассчитывается по формуле

,

где t – коэффициент доверия, зависящий от вероятности, с которой можно гарантировать, что предельная ошибка не превысит t -кратную среднюю ошибку, т. е. всегда будет выполняться неравенство

.

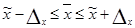Значения коэффициента доверия при соответствующей вероятности:

Вероятность, %	68,3	95,0	95,4	99,0	99,7	99,9
Коэффициент доверия, t	1,00	1,96	2,00	2,58	3,00	3,28

Виды методов отбора единиц в выборочную совокупность: повторный и бесповторный.

Виды способов организации отбора единиц в выборочную совокупность: собственно-случайный; механический; типический; серийный.

Формулы для расчета средней ошибки выборки:

Вид отбора	Метод отбора	Средняя ошибка выборки
для средней	для доли
Собственно-случайный	повторный
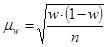
	бесповторный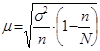

О к о н ч а н и е

Механический	повторный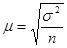
бесповторный
Типический	повторный
бесповторный
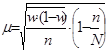
Серийный	повторный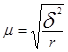
бесповторный

где – дисперсия выборочной совокупности;

N – число единиц генеральной совокупности;

n – число единиц выборочной совокупности;

w – доля единиц совокупности, обладающих данным альтернативным признаком в выборочной совокупности;

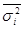– средняя из внутригрупповых дисперсий;

r – число отобранных серий;

R – число серий в генеральной совокупности;

– межгрупповая дисперсия;

– средняя из внутригрупповых дисперсий для доли;

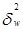– межсерийная дисперсия для доли.

Пример 1. В городе проживает 250 тыс. семей. Для определения среднего числа детей в семьях города была организована 2%-ная случайная бесповторная выборка семей. Получено распределение семей:

Число детей в семье, чел.	Количество семей, единиц
	2 500
	1 200
Итого	5 000

С вероятностью 99,9% определить пределы, в которых находится среднее число детей в семьях города.

Решение. Все предварительные расчеты представим в таблице:

Число детей,	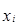Количество семей,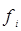
	2 500	2 500	2 500
	1 200	2 400	4 800
		1 200	3 600
			1 600
Итого	5 000	6 500	12 500

Рассчитаем среднюю величину и дисперсию выборочной совокупности

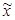
= 1,3 чел.

= 2,5.

= = 2,5 – (1,3)² = 0,81.

Вычислим предельную ошибку выборки

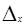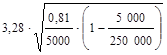= = = 0,0126 (чел.).

Находим пределы генеральной средней величины

1,3 – 0,0126 1,3 + 0,0126,

т. е. с вероятностью 99,9% можно утверждать, что в среднем на каждые три семьи в городе приходится 4 ребенка.

Пример 2. Проводился 10% бесповторный типический отбор работников предприятия с целью оценки потерь из-за временной нетрудоспособности. Получены следующие результаты обследования:

№ отдела	Численность работников, чел.	Обследовано, чел.	Число дней временной нетрудоспособности за год
средняя	дисперсия
	2 000
	3 000
	1 000

С вероятностью 95,4 определить предельную ошибку выборки.

Решение. Вычислим среднюю величину в выборочной совокупности

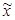
= 14,5 дней.

Определим среднюю из внутригрупповых дисперсий

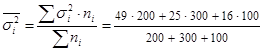= 31,5.

Предельная ошибка выборки рассчитывается следующим образом:

= 0,435 (дней),

т. е. с вероятностью 95,4% можно сделать вывод о том, что среднее число дней временной нетрудоспособности одного работника в целом по предприятию находится в пределах от 14,065 до 14,935 дней.

Необходимая численность единиц выборочной совокупности определяется из соответствующих соотношений, используемых при расчете предельных ошибок выборки.

Виды выборки	Повторный отбор	Бесповторный отбор
Собственно случайная Механическая	n =	n =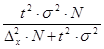
Типическая	n =	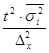n =
Серийная	n =	n =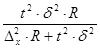

Пример 3. В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического бесповторного отбора.

Каков должен быть объем выборки, чтобы с вероятностью 68,3% предельная ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225?

Решение. Определим необходимую численность выборки

агентств.

Для проведения обследования должно быть отобрано не менее 20 агентств.

Задания для самостоятельного решения

1.При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 500 изделий. В результате был установлен средний вес изделия 45 кг при среднеквадратическом отклонении 2 кг.

С вероятностью 99,9% определите пределы, в которых находится средний вес изделия в генеральной совокупности.

2.Для определения средней величины расходов на полугодовую подписку вся совокупность семей города была разбита по уровню дохода на три группы. После проведения 5%-ного обследования получены следующие результаты:

№ группы	Число семей	Средние расходы на подписку, руб.	Групповые дисперсии
		1 200 2 000	16 000 40 000

С вероятностью 99,9% определите пределы, в которых находится средняя величина расходов на полугодовую подписку в семьях города.

3.На предприятии случайным бесповторным образом производилось обследование 300 работников из общей численности работающих (1500 чел.) с целью изучения средней месячной заработной платы. В результате обследования получены следующие данные:

Группы работников по размеру заработной платы, руб.	До 10	10–15	15–25	25 и более
Число работников, чел.

Определите:

а) с вероятностью 99,7% пределы, в которых находится средний размер месячной заработной платы одного работника предприятия;

б) с вероятностью 95,4% долю работников, имеющих размер месячной заработной платы не более 15 000 руб.

4.На городской телефонной станции из 20 000 абонентов в порядке собственно случайной повторной выборки проведено 100 наблюдений и установлено, что средняя продолжительность одного телефонного разговора составляет 18 мин. при среднеквадратическом отклонении 7 мин.

С вероятностью 99,9% определите пределы средней продолжительности разговора в генеральной совокупности.

5.На предприятии выборочно проверен трудовой стаж у работников. Результаты типического бесповторного обследования следующие:

Группы работников	Численность работников, чел.	Средний стаж работы, лет	Среднее квадратическое отклонение стажа, лет
Мужчины Женщины

С вероятностью 95,4% определите пределы среднего трудового стажа работников в генеральной совокупности, если обследовано 25% от общей численности работающих.

6.С целью прогнозирования урожайности риса в хозяйствах региона была проведена 20%-ная серийная выборка, в которую вошли пять хозяйств. Средняя урожайность риса в обследованных хозяйствах составила (ц/га): 26; 27; 22; 28; 25.

С вероятностью 99,9% определите пределы, в которых находится средняя урожайность риса в регионе.

7.Для определения среднего ежедневного времени занятости семейных женщин в домашнем хозяйстве проведена типическая 10%-ная бесповторная выборка, которая дала следующие результаты:

Возраст женщин, лет	Численность женщин в группе, чел.	Частные средние	Частные дисперсии
до 25 25–45 свыше 45		2,0 3,5 3,2	4,0 6,8 5,0

С вероятностью 95,4% определите средние затраты времени семейных женщин на работу по дому для всей совокупности семейных женщин.

8.В одном из институтов проводилось 10%-ное механическое бесповторное обследование абитуриентов по количеству баллов, полученных на вступительных экзаменах в 2006 г. (цифры условные). Результаты обследования следующие:

Количество баллов
Число абитуриентов, чел.

Определите:

1) с вероятностью 99,9% пределы, в которых находится среднее количество баллов, полученное абитуриентами при поступлении в учебное заведение;

2) с вероятностью 95,4% долю абитуриентов, получивших на вступительных экзаменах более 260 баллов.

9.Для определения скорости расчетов с кредиторами 500 организаций региона в коммерческом банке необходимо провести выборочное обследование методом механического бесповторного отбора. Определите необходимый объем выборки, чтобы с вероятностью 99,7% ошибка среднего значения выборки не превышала 3-х дней, если по данным пробного обследования среднее квадратическое отклонение составило 10 дней.

10.На хлебозаводе № 28 было проведено механическое повторное обследование партии поступившей муки. Из 5 000 мешков было обследовано 250 мешков, в 200 из которых оказалась мука высшего сорта. С вероятностью 99,9% определите возможный процент мешков с мукой высшего сорта во всей поступившей партии.

11.При обследовании 500 пар женской обуви, отобранных из партии готовой продукции магазина в случайном порядке, 40 пар оказались бракованными. С вероятностью 95,4% определите предел, в котором находится доля бракованной обуви, продаваемой магазином.

12.На предприятии с численностью работников 15 тыс. чел. в порядке механической бесповторной выборки предполагается определить долю работников со стажем работы 10 лет и более.

Определите необходимую численность выборки, чтобы с вероятностью 99,7% ошибка выборки не превышала 0,03, если на основе предыдущих обследований известно, что дисперсия равна 0,2?

Контрольные вопросы

1. Для чего проводится выборочное наблюдение и в чем оно заключается?

2. Перечислите виды и способы выборочного наблюдения. В чем они заключаются?

3. Что характеризует средняя и предельная ошибки выборки? Как они рассчитываются?

4. Как определяется необходимая численность единиц выборочной совокупности?

Дата добавления: 2014-11-25