Средства архивации информации

Иногда резервные копии информации приходится выполнять при общей ограниченности ресурсов размещения данных, например владельцам персональных компьютеров. В этих случаях используют программную архивацию. Архивация это слияние нескольких файлов и даже каталогов в единый файл — архив, одновременно с сокращением общего объема исходных файлов путем устранения избыточности, но без потерь информации, т. е. с возможностью точного восстановления исходных файлов. Действие большинства средств архивации основано на использовании алгоритмов сжатия, предложенных в 80-х гг. Абрахамом Лемпелем и Якобом Зивом. Наиболее известны и популярны следующие архивные форматы:

ZIP, ARJ для операционных систем DOS и Windows;

TAR для операционной системы Unix;

межплатформный формат JAR (Java ARchive);

RAR (все время растет популярность этого нового формата, так как разработаны программы позволяющие использовать его в операционных системах DOS, Windows и Unix).

Пользователю следует лишь выбрать для себя подходящую программу, обеспечивающую работу с выбранным форматом, путем оценки ее характеристик – быстродействия, степени сжатия, совместимости с большим количеством форматов, удобности интерфейса, выбора операционной системы и т.д. Список таких программ очень велик – PKZIP, PKUNZIP, ARJ, RAR, WinZip, WinArj, ZipMagic, WinRar и много других. Большинство из этих программ не надо специально покупать, так как они предлагаются как программы условно-бесплатные (Shareware) или свободного распространения (Freeware). Также очень важно установить постоянный график проведения таких работ по архивации данных или выполнять их после большого обновления данных.

Вопрос 35. Дать определение позиционным и непозиционным системам счисления. Дать определение понятию "система счисления".

Теоретической основой кодирования чисел является подробным образом развитая в математике теория систем счисления. Система счисления — это способ записи чисел с помощью фиксированного числа знаков. Последние имеют общепринятое название — цифры.

Системы счисления весьма разнообразны. Прежде всего, они делятся на позиционные и непозиционные. Позиционной называется система счисления, в которой количественный эквивалент цифры зависит от ее положения в записи числа; в противном случае система является непозиционной. Большинство используемых на практике систем позиционно, поскольку именно для них обеспечивается наиболее простая арифметика.

В частности, используемая в быту система представления чисел позиционная (сравните значение цифры 2 в записи чисел 132 и 123!). Что же касается непозиционных систем, то сюда относятся хорошо известный римский способ записи чисел, а также унарная система, с которой вы, вероятно, встречались в первом классе (вспомните счетные палочки!).

В основе большинства систем счисления лежит принцип разложения по степеням некоторого целого числа², которое называется основанием системы счисления. Для используемой в быту системы основанием служит число 10 и его степени (сотни, тысячи и т.д.); математики называют ее десятичной, или системой счисления с основанием 10. Попутно заметим, что для построенных рассматриваемым традиционным способом систем счисления основание равняется количеству различных цифр, требуемых для изображения произвольных чисел.

Важно понимать, что десятичная система счисления лишь одна из возможных и не имеет никаких принципиальных преимуществ перед системами с другими основаниями. Например, двенадцатеричная денежная система значительно удобнее десятичной: английский шиллинг удается поровну разделить между двумя, тремя, четырьмя, шестью и двенадцатью людьми, тогда как 10 рублей справедливо распределяется только на двоих, пятерых или десятерых.

Для производства электронной вычислительной техники значительное удобство представляет двоичная система. Для инженеров существенно проще создать электронные элементы с двумя устойчивыми состояниями, соответствующими базовым цифрам системы 0 и 1. Кроме того, все арифметические и логические (булевские) операции наиболее просто реализовываются именно на двоичной основе, а их теория разработана в мельчайших деталях. Заметим, что на преимущества двоичной системы при разработке ЭВМ Джон фон Нейман указывал в своей классической работе еще в 1946 году.

Кроме перечисленных достоинств, двоичная система имеет, конечно, и недостатки, среди которых в первую очередь необходимо назвать необходимость перевода данных из “человеческой” (десятичной) системы счисления в “машинную” (двоичную) и обратно, а также громоздкость записи двоичных чисел. Рассмотрим названные проблемы подробнее.

Поскольку с математической точки зрения системы счисления с любыми основаниями равноправны, существует единый алгоритм перевода чисел из одной системы счисления в другую. Он заключается в последовательном делении рассматриваемого числа на основание системы счисления. К сожалению, алгоритм требует проведения арифметических действий в той системе счисления, в которой представлено исходное число, поэтому удобен лишь для перевода из десятичной системы в произвольную, но не наоборот.

Частным случаем указанного выше способа является перевод из десятичной системы счисления в двоичную, который нужен, чтобы узнать представление в компьютере произвольного десятичного числа. Опуская подробности, напомним, как выглядит процесс перевода числа 20₁₀ в двоичный код:

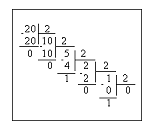
Остается “собрать” итоговое двоичное число из остатков от деления, не забывая при этом, что старшие разряды получаются всегда позднее, чем младшие. В итоге получим: (20)₁₀ = (10100)₂.

Что касается обратного перевода из двоичной системы в десятичную, то универсальный алгоритм деления на основание системы здесь также возможен, но, как уже говорилось, его непосредственная арифметическая реализация неудобна. Поэтому на практике используется иной алгоритм, базирующийся на другом универсальном свойстве, о котором уже упоминалось в связи с определением основания системы счисления. Речь идет о том, что запись произвольного числа в любой системе счисления суть его разложение по степеням основания. Для интересующего нас сейчас случая двоичной системы вычисления будут выглядеть, например, так:

(10100)₂ = 1 x 2⁴ + 0 x 2³ + 1 x 2² + 0 x 2¹ + 0 x 2⁰ = 16 + 4 = (20)₁₀.

Подчеркнем, что в приведенных выше примерах рассматривалась связь десятичной системы именно с двоичной только потому, что последняя применяется в компьютерах. С математической точки зрения, вместо двоичной можно взять систему с любым другим основанием.

Обратимся теперь к проблеме громоздкости двоичного кода. Если посмотреть на двоичное число, представляющее собой представление некоторого десятичного с весьма умеренным числом цифр (например, трех- или четырехзначного числа), то обнаружится, что выглядит это чрезмерно длинно. Более того, длинная “однообразная” цепочка из нулей и единиц очень плохо воспринимается глазами. Чтобы облегчить ситуацию, для более компактной записи используется восьмеричная или шестнадцатеричная система счисления. Особенностью данных оснований является тот факт, что и 8, и 16 есть степени двойки, а значит, перевод между ними и двоичной системой максимально прост. Учитывая, что 8 = 2³, а 16 = 2⁴, получаем, что каждая восьмеричная цифра объединяет ровно 3 двоичных разряда, а шестнадцатеричная — 4.

Отсюда немедленно следует алгоритм перевода из двоичной системы в восьмеричную (шестнадцатеричную):

сгруппировать двоичные разряды справа налево по три (четыре); если в старшей (т.е. самой левой) группе битов не хватает, их можно дополнить слева незначащими нулями;

заменить каждую из полученных групп соответствующей ей восьмеричной (шестнадцатеричной) цифрой.

Например:

11010₂ = 0001 1010 = 1A₁₆.

Обратный переход еще проще: достаточно каждую восьмеричную (шестнадцатеричную) цифру заменить ее двоичным представлением, дополняя его при необходимости до трех (четырех) двоичных цифр нулями слева.

Для облегчения процессов перевода удобно составить таблицу соответствия между восьмеричными или шестнадцатеричными цифрами и их двоичными кодами.

Остается обсудить вопросы, связанные с двоичной арифметикой. Отметим, что арифметические действия в системах счисления с любыми основаниями производятся по одинаковым правилам. Единственное отличие состоит в том значении, при превышении которого возникает перенос в следующий разряд. В общепринятой десятичной системе “критическое” значение равно 10 (вспомните: “8 + 7 = 15, 5 пишем, 1 в уме”).
В двоичной системе, где нет никаких цифр, кроме 0 и 1, перенос наступает, когда в разряде получается результат, равный 2 (или больше). Нетрудно сообразить, что минимальное значение, при котором возникает перенос, равно количеству цифр и, следовательно, основанию системы счисления.

В свете последнего вывода можно сформулировать правила арифметических операций, которые не зависят от применяемой системы счисления. Покажем, как это сделать на примере сложения.

Сложение двух чисел в системе счисления с основанием N осуществляется поразрядно от младших разрядов к старшим (“справа налево”, если смотреть на запись числа). Когда сумма данного разряда S не превышает значения N, результат сложения является окончательным. Если же S N, то происходит перенос в старший (“более левый”) разряд, причем каждая единица переноса уменьшает значение S на величину N.

Вопрос 36. Определение понятия "векторная графика". Определение понятия "растровая графика".

Существует три вида компьютерной графики:
Растровая графика
Векторная графика

Фрактальная графика
Растровое изображение, цифровое изображение - это файл данных или структура, представляющая прямоугольную сетку пикселей или точек цветов на компьютерном мониторе, бумаге и других отображающих устройствах и материалах. То есть, растровая графика - это формат изображения, который содержит информацию о расположении, количестве и цвете пикселей.
Главным достоинством растровой графики является создание (воспроизведение) практически любого рисунка, вне зависимости от сложности, в отличие, например, от векторной, где невозможно точно передать эффект перехода от одного цвета к другому (в теории, конечно, возможно, но файл размером 1 МБ в формате BMP будет иметь размер 200 МБ в векторном формате).
Векторная графика (другое название - геометрическое моделирование) - это использование геометрических примитивов, таких как точки, линии, сплайны и многоугольники, для представления изображений в компьютерной графике. Термин используется в противоположность к растровой графике, которая представляет изображения как матрицу пикселей (точек).
Изначально человеческий глаз воспринимает изображение подобно растровому образу. Картинка проецируется на сетчатку, состоящую из отдельных, реагирующих на свет клеток. Далее система глаз-мозг распознаёт в изображении отдельные объекты, геометрические фигуры, которые уже легче обрабатывать и запоминать.
Фрактальная графика основана на математических вычислениях. Базовым элементом фрактальной графики является сама математическая формула, то есть никаких объектов в памяти компьютера не хранится и изображение строится исключительно по уравнениям. Таким способом строят как простейшие регулярные структуры, так и сложные иллюстрации, имитирующие природные ландшафты и трехмерные объекты.

Вопрос 37. Понятие термина "текст", как информационный объект. Основные типа текстовых редакторов.

Текст (от лат. textus «ткань; сплетение, связь, сочетание») — в общем плане связная и полная последовательность знаков.

Существуют две основных трактовки понятия «текст»: «имманентная» (расширенная, философски нагруженная) и «репрезентативная» (более частная). Имманентный подход подразумевает отношение к тексту как к автономной реальности, нацеленность на выявление его внутренней структуры. Репрезентативный — рассмотрение текста как особой формы представления знаний о внешней тексту действительности.

Работа с текстом осуществляется с помощью так называемых текстовых редакторов -компьютерных программ, предназначенных для создания и изменения текстовых файлов, а также их просмотра на экране, вывода на печать, поиска фрагментов текста и т. п.

Дата добавления: 2014-11-25