
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение типовых примеров для контрольной работы № 1 1 страница
|
|
|
|
ВВЕДЕНИЕ
Настоящее пособие предназначено для студентов заочного отделения. Пособие содержит образцы решения задач, задания для контрольных работ, вопросы к экзамену и список литературы.
При выполнении контрольных работ следует руководствоваться следующими указаниями.
1. Каждую работу следует выполнять в отдельной тетради, на обложке которой должны быть указаны фамилия и инициалы студентов, полный шифр, номер контрольной работы. Решения всех задач и пояснения к ним должны быть достаточно подробными. Все вычисления (в том числе и вспомогательные) необходимо делать полностью. Чертежи и графики должны быть выполнены аккуратно и четко с указанием масштаба, координатных осей и других элементов чертежа. Объяснения к задачам должны соответствовать тем обозначениям, которые даны на чертеже.
2. После получения работы (как зачтенной, так и незачтенной) студент должен исправить в ней все отмеченные рецензентом недостатки. В случае незачета студент обязан в кратчайший срок выполнить все требования рецензента и представить работу на повторное рецензирование, приложив при этом первоначально выполненную работу.
4. Студент выполняет тот вариант контрольных работ, который совпадает с двумя последними цифрами его учебного шифра.
Задание № 1 Вычислить пределы
1) 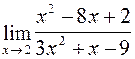 ; 2)
; 2) 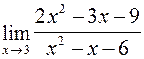 ,
,
3)  , 4)
, 4)  .
.
Решение.
1)  .
.
2) 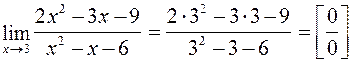 , при подстановке вместо переменной х ее предельного значения 3 получается неопределенность вида
, при подстановке вместо переменной х ее предельного значения 3 получается неопределенность вида  . Для избавления от этого типа неопределенности в нашем случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой
. Для избавления от этого типа неопределенности в нашем случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой
ax 2 + bx + c = a (x – x 1)∙(x – x 1),
где х 1, х 2 – корни квадратного трехчлена ax 2 + bx + c.
У нас  , так как дискриминант квадратного трехчлена
, так как дискриминант квадратного трехчлена  а следовательно, х 1 = 3,
а следовательно, х 1 = 3,  . Аналогично x 2 – x – 6 = (x - 3)∙(x + 2).
. Аналогично x 2 – x – 6 = (x - 3)∙(x + 2).
Теперь условие примера можно переписать в другом виде и продолжить решение:
 ;
;
3) 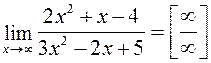 .
.
Здесь сталкиваемся с неопределенностью  , избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби старшей степени переменной:
, избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби старшей степени переменной:
 ;
;
4) 
В данном случае для освобождения от неопределенности будем использовать первый замечательный предел и одно из его очевидных следствий:
 ;
;  .
.
Решение примера будет выглядеть следующим образом:
 Задание № 2 Найти производные функций
Задание № 2 Найти производные функций
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
При решении всех последующих примеров на нахождение производных будут использованы известные правила дифференцирования суммы, разности, произведения, дроби и теорема о производной сложной функции:
а)  ;
;
б)  ;
;
в) 
г) если задана сложная функция y = f (u), где u = j (x), то есть y = f (j (х)); если каждая из функций y = f (u) и u = j (x) дифференцируема по своему аргументу, то

Решение.
1)  ,
, 


2) 


 ;
;
3) 

 ;
;
4) 

 .
.
Задание № 3
Исследовать функцию и построить график
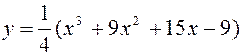 .
.
Решение.
1) Областью определения данной функции являются все действительные значения аргумента х,то есть
D (y):  а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.
а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.
2) Исследуем функцию на интервалы монотонности и экстремумы. С этой целью найдем ее производную и приравняем нулю:
 .
.
Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки 1 рода х 1 = - 5, х 2 = - 1. Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:
| х | 
| -5 | (-5, -1) | -1 | 
|

| + | — | + | ||
| f (x) | 
| max | 
| min | 
|
 .
.
3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:
 .
.
Итак, функция имеет одну критическую точку 2 рода
х = -3;. разобьем область определения полученной точкой на части, в каждой из которых установим знак второй производной:
| x | 
| -3 |  
|

| — | + | |
| f (x) | 
| т.п. | |
Значение х = - 3 является абсциссой точки перегиба графика функции, а ордината этой точки
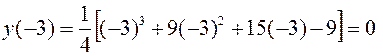 .
.
4) Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты
y = kx+b воспользуемся формулами
 .
.
 .
.
Таким образом, у графика заданной функции наклонных асимптот нет.
5) Для построения графика изобразим точки максимума
А 1(- 5; 4), минимума А 2(- 1 - 4), перегиба А 3(-3; 0) и точку
А 4(0;  ). пересечения графика с осью Оу.
). пересечения графика с осью Оу.

|
С учетом результатов предыдущих исследований построим кривую (см. рис. 2).
Рисунок2
Задания к контрольной работе № 1
Задание 1
Найти указанные пределы:

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |
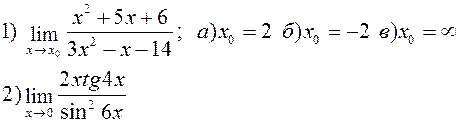
| |

| |

| |

| |

| |

| |

| |

| |
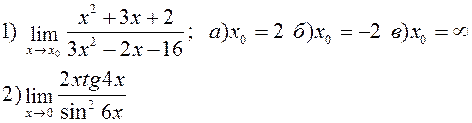
| |

| |

| |

| |

| |

|
Задание № 2
Найти производные, пользуясь правилами и формулами дифференцирования:
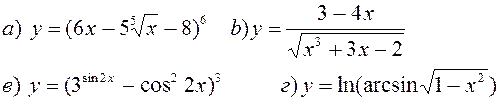
| |

| |

| |

| |

| |

| |

| |

| |
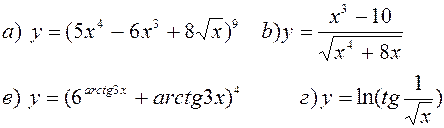
| |

| |
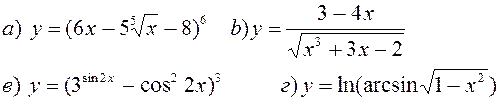
| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

|
Задание № 3
Исследовать заданные функции методами дифференциального исчисления, начертить их графики.
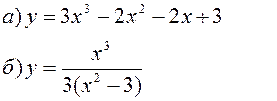
| |

| |

| |

| |

| |

| |
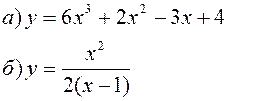
| |

| |

| |

| |
 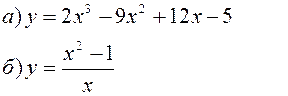
| |
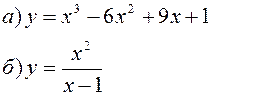
| |

| |

| |
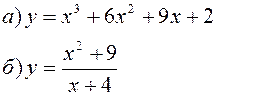
| |

| |

| |

| |

| |
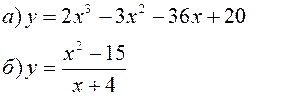
| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

|
Решение типовых примеров для контрольной работы № 2.
Задание № 1
1. Найти неопределенный интеграл 
Решение. Применим подстановку  , тогда
, тогда  и
и
 ;
;
2. Найти интеграл  .
.
Решение. Применим подставку t =3 x 3 – 5.
Тогда 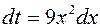 ;
;  , откуда
, откуда
 .
.
Задание № 2
Найти интеграл 
Решение. Преобразуем знаменатель дроби, стоящей под знаком интеграла следующим образом:
x 2 – 6 x +13 = x 2 – 6 x + 9 + 4 = (x - 3)2 + 22. Тогда после подстановки t = x - 3 получаем
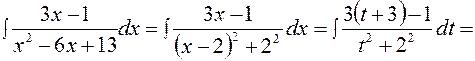

 причем, при вычислении интеграла
причем, при вычислении интеграла  воспользуемся заменой переменной z = t 2+4, тогда dz = 2 tdt, откуда
воспользуемся заменой переменной z = t 2+4, тогда dz = 2 tdt, откуда
 .
.
Итак, учитывая, что t = x – 3, имеем

 .
.
Задание № 3
1. Найти интеграл 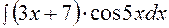 .
.
Решение. Применим формулу интегрирования по частям

Положим
u = 3 x +7, dv = cos5 xdx,
тогда
du = 3 dx,  .
.
Следовательно,

 .
.
2. Найти интеграл  .
.
Решение.
Положим
u = arctg 4 x, dv = dx,
тогда
 v = x.
v = x.
Отсюда
 .
.
Применяя в последнем интеграле подстановку t = 1+16 x 2,
получаем,  , следовательно,
, следовательно,
 .
.
Отсюда  .
.
Задание № 4
Вычислить площадь, ограниченную параболами
y = 2 x 2 – x – 2,
y = - x 2 + x – 1.
Решение.
Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:
2 x 2 – x – 2 = - x 2 + x – 1. Отсюда 3 x 2 – 2 x – 1 = 0, D = 4 + 4∙3 = 16,

|
Рисунок 3
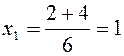 ,
, 
Вычисление площади осуществляем по формуле:
 ,
,
где f 1(x), f 2(x) – кривые, ограничивающие фигуру (f 2(x) ³ f 1(x)).
В нашем случае


Задания к контрольной работе № 2
Задание №1
Найти неопределенные интегралы способом подстановки (методом замены переменной)

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Задание №2
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 1281; Нарушение авторских прав?; Мы поможем в написании вашей работы!