Краткое теоретическое введение

Аппаратура

Цель и содержание работы

МОЛЕКУЛЫ CN

ИЗУЧЕНИЕ СТРУКТУРЫ МОЛЕКУЛЯРНОГО СПЕКТРА И ОПРЕДЕЛЕНИЕ МЕЖАТОМНОГО РАССТОЯНИЯ

Ознакомление с электронно – колебательно – вращательными спектрами (полосатые спектры) двухатомных молекул и методикой расшифровки их колебательно – вращательной структуры на примере спектра испускания молекулы CN, возбуждаемого в электрической дуге. Ознакомление с системой энергетических состояний, связанных с электронным движением, колебанием и вращением двухатомной молекулы. Определение молекулярных постоянных 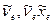и оценка энергии диссоциации. Измерение вращательной структуры колебательной полосы с целью определения межъядерного расстояния.

Освоение методики работы на спектрографе ДФС – 8 и измерения спектральных линий и кантов в спектре.

Спектрограф ДФС – 8, электрическая дуга переменного тока (генератор УГЭ – 4), измерительный микроскоп МИР – 12, спектропроектор ПС – 18, атлас спектральных линий.

Молекулярные спектры значительно сложнее и разнообразные атомных. Это связано с тем, что в случае молекулы существенно увеличивается число факторов, от которых зависит ее энергия в том или ином квантовом состоянии. Энергия простейшей двухатомной молекулы Е_мол складывается из трех компонентов: 1) энергии Е_е электронной оболочки молекулы; 2) энергии 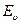колебаний ядер атомов вдоль соединяющей их прямой; 3) энергии E _r вращения ядер вокруг общего центра масс. Все эти компоненты энергии дискретны, квантованы. Таким образом,

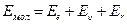(9.1)

при этом Е_е » 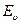»E _r

Наибольшие изменения энергии молекулы происходят при изменении состояния ее электронной оболочки. Электронная оболочка молекулы образуется в результате объединения оболочек атомов и электронные состояния молекулы аналогичны электронным состояниям атомов, (но не тождественны, т.к. межатомные взаимодействия оказывают сильное влияние на энергию системы). Естественно, что символика электронных состояний молекул во многом сходна с символикой атомных состояний. Аналогична орбитальному квантовому числу электрона l или орбитальному квантовому числу многоэлектронного атома L для молекулы вводится квантовое число Л, определяющее (в единицах h) абсолютное значение проекции результирующего орбитального момента «электронного облака» на преимущественное направление. Преимущественным направлением для молекулы является направление ее оси, т.е. прямая, соединяющая центры ядер. Далее, аналогично обозначению символами S, P, D энергетических состояний атома, соответствующих значениям L=0, 1, 2…, для энергетических состояний молекулы с Л=0, 1,2… используют символы S, P, D и т.д.

Вместе с тем S (как и S при описании энергетических состояний атома) служит для обозначения молекулярного спинового квантового числа, характеризующего абсолютное значение проекции результирующего спина электронов на ось молекулы. Подобным внутреннему квантовому числу атома в символике энергетических состояний молекулы является квантовое число W, определяющее проекцию на ось молекулы полного момента ее электронной оболочки. Таким образом,

W=Л±S.

Так же как у атомов, у молекул наблюдается расщепление энергетических уровней, связанное с различным значением и различной ориентацией результирующего спина относительно результирующего орбитального момента и определяемое выражением 2 S+1.

Используя эти обозначения, электронное состояния молекулы характеризует символом: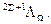

Здесь Л показывает, что в символе представляется одно из обозначений: S, P или D, характеризующих величину квантового числа Л.

Как и для атомов, для молекул существуют правила отбора, ограничивающие возможности переходов из одних электронных состояний в другие. Разрешенными являются переходы с _D Л=0,±1,_D S=0 и _D W=0,±1.

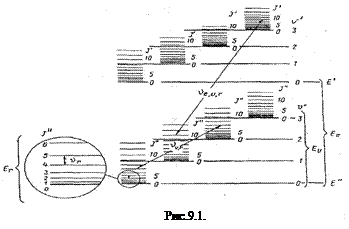
В формуле (9.1) каждый член принимает определенные значения. При заданных Е_е, 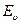,E _r полная энергия Е молекулы имеет значение, соответствующее определенному электронно – колебательно – вращательному состоянию. Получается совокупность далеко раздвинутых электронных уровней, более тесно расположенных колебательных уровней и еще более близко расположенных вращательных уровней (рис. 9.1).

При переходе молекулы из одного состояния в другое могут одновременно изменяться все три части полной энергии – электронная, колебательная и вращательная. Спектры излучения и поглощения молекул в своем составе содержит три выраженные структуры – электронную, колебательную и вращательную. Для переходов с излучением и поглощением, согласно условию частот, имеем

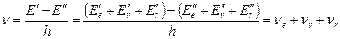, (9.2)

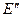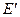где и – энергии нижнего и верхнего электронно – вращательного уровней соответственно, причем

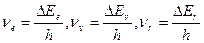(9.3)

характеризует колебательную (полосатую) структуру спектра; 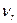вращательную (тонкую) структуру.

Изменение электронной энергии сопровождается одновременным изменением колебательной и вращательной энергий. При этом получаются электронно – колебательно – вращательные спектры, которые сокращенно называется электронными спектрами. Отдельные полосы в этих спектрах соответствуют различным значениям 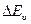при заданном 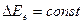, а отдельные линии тонкой структуры в полосах – различным значениям 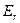при заданных 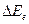и .

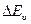Разность между электронными уровнями 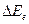порядка 1-10 эВ. Переходы между ними дают излучение с частотами порядка 10¹⁴ -10¹⁵ Гц, т.е. подобные спектры расположены в видимой и ультрафиолетовой областях спектра.

Если 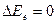, т.е. электронное состояние постоянно, то при изменении колебательной энергии возникают колебательные спектры. Изменение колебательной энергии в этом случае сопровождается изменением вращательной энергии, т.е.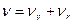

Для колебательных уровней ~10^-1 – 1 эВ и получаемые при переходах частоты излучения составляют ~10¹² – 10¹⁴ Гц. Спектры излучения и поглощения расположены в ближней и дальней ИК области.

Есл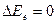и и 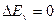изменяется только вращательная энергия, то возникают чисто вращательные спектры. 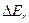~10^-3 – 10^-2 эВ и соответствует частоте излучения 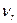~10¹¹ – 10¹² Гц. Чисто вращательные спектры расположены в далекой ИК и субмиллиметровой областях спектра.

9.3.1.Вращательные спектры. В первом приближении двухатомную молекулу будем рассматривать как жесткий ротатор с массами m₁ и m₂ и расстоянием между центрами тяжести атомов r (рис.9.2.). Для модели жесткого ротатора энергетические состояния молекулы описываются формулой

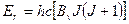(9.4)

терм вращательной энергии

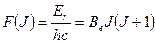(9.5)

где

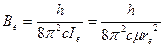(9.6)

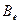– вращательная постоянная, в м^-1, относящаяся к минимуму кривой потенциальной энергии; 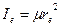момент инерции в кгм², 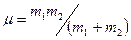– приведенная масса в кг; (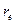) – межъядерное расстояние в м; J=0, 1. 2… вращательное квантовое число.

Таким образом, энергетические состояния молекулы зависят от ее приведенной массы и межъядерного расстояния. Из уравнений (9.4),(9.2) с учетом правила отбора следует

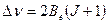(9.7)

Разность волновых чисел двух соседних линий во вращательном спектре равна

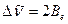(9.8)

Отсюда экспериментально может быть найдена молекулярная константа – момент инерции. Зная массу атомов, по уравнению 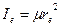можно рассчитать другую молекулярную константу – межъядерное расстояние.

9.3.2.Колебательно–вращательные спектры. Термы колебательно – вращательных состояний являются суммой термов колебательных и вращательных состояний

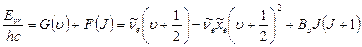(9.9)

где 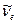– волновое число колебаний см^-1; 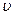– колебательное квантовое число, принимающее значение 0,1,2,…;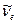 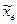– коэффициент ангармоничности колебаний см^-1.

1) для упрощения рассмотрения пренебрегаем пока вращательной структурой и рассматриваем только колебательные переходы. Основной тон (основная полоса) соответствует переходу 1-0 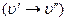. Переходы 2-0, 3-0 и т.д. называются обертонами. Частоты колебаний см^-1 обертонов легко получить из разности термов

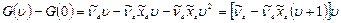(9.10)

Из значений частот обертонов и основной частоты можно вычислять колебательные частоты 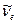и ангармоничности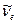 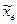. Для этого сначала вычисляются первые разности между первым обертоном и основной частотой, вторым обертоном и первым обертоном и т.д.

В общем виде первые разности равны

(9.11)

и по своему физическому смыслу представляют собой расстояние между соседними термами колебательных состояний.

Если по первым разностям 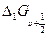определить вторые разности

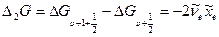(9.12)

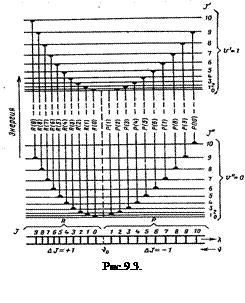то тогда можно вычислить постоянную ангармоничности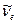 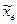, а, зная ее, по формуле (9.11) определить колебательную частоту 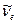см^-1.

2) рассмотрим вращательную структуру колебательно–вращательных спектров (рис.9.3.). По правилам отбора , и поэтому осуществляются две серии переходов между вращательными состояниями разных колебательных уровней. Соответственно и в спектре наблюдаются две серии линий, которые называются ветвями полос: R – ветвями, если 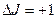, и Р – ветвями, если 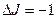. Между сериями Р и R – ветвей находится так называемый нулевой промежуток (начало полосы) 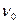. Он соответствует число колебательному переходу 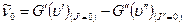, который запрещен правилами отбора, т.к. для него 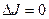. Поэтому отсчет Р – линий начинается с 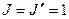. Ветвь R всегда расположена со стороны больших частот от 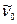, а первая наблюдаемая линия соответствует J=0.

Линии R – ветви, для которой 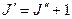, можно представить уравнением

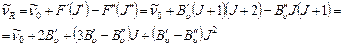(9.13)

где 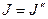=0,1,2,…. Соответственно для Р – ветви, для которой ,

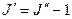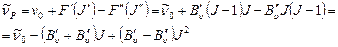, (9.14)

где 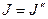=1, 2, 3, ….

3) 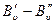мала, и приняв 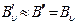имеем

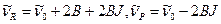
В этом приближении расстояние между двумя соседними линиями вращательной структуры равно 2В, как и в чисто вращательных спектрах.

9.3.3. Электронно–колебательно–вращательные спектры. В общем виде систему всех возможных энергетических состояний двухатомной молекулы можно представить уравнением

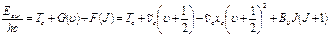(9.15)

где T_e – терм чисто электронного возбуждения, который для основного электронного состояния равен нулю.

Остановимся только на колебательной структуре электронных спектров. В этом случае положение колебательных полос описывается следующим уравнением:

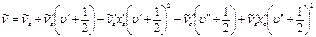, (9.16)

где 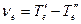– чисто электронный переход.

Никаких правил отбора на переходы с разными значениями 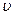не накладывается.

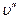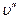Серии полос с постоянными значением называются прогрессиями по , а с постоянными – прогрессиями по . Серии полос с постоянными значением 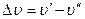называются диагональными сериями.

Все наблюдаемые в спектре полосы, принадлежащие одному электронному переходу, можно представить в виде так называемой таблицы Деландра.

По таблице Деландра можно довольно просто произвести расчет значени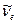й и 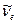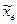для основного и возбужденного электронного состояний и величину электронного возбуждения .

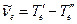Чтобы рассмотреть тонкую (вращательную) структуру полос, связанную с изменением вращательных состояний молекул, следует принять постоянной величину

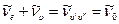
Тогда вращательная структура электронно – колебательно – вращательной полосы опишется уравнением

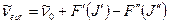, (9.17)

которое подобно уравнениям (9.13,9.14) в случае колебательно – вращательных спектров.

При расшифровке тонкой вращательной структуры электронно – колебательно – вращательных спектров можно определить вращательные постоянные 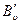и 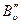, а из них и межъядерные расстояния молекул в основном и возбужденных электронных состояниях.

Энергия диссоциации двухатомных молекул. Энергия диссоциации – очень важная характеристика молекулы, особенно при определении частот реакций различных химических процессов. Энергию диссоциации двухатомных молекул можно определить по приближенной формуле линейной экстраполяции

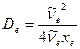(9.18)

Это выражение можно получить исходя из того, что колебательные интервалы 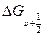(9.11) линейно зависят от 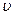и стремятся к нулю при приближении 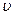к своему максимальному значению . Поэтому можно принять, что

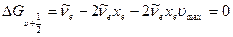
откуда

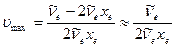(9.19)

т.к. 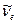x_e «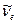

Подставляя в выражение для энергии термов (9.9), можно определить энергию, при которой происходит диссоциация молекулы

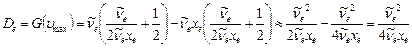
Следует заметить, что формула (9.18) довольно приближенная и дает точность ~20%.

При переходе молекул из возбужденного вращательно – колебательно – электронного состояния на различные вращательно – колебательные подуровни нулевого электронного уровня происходит излучение кванта света с энергиями, равными разности энергий более высокого и более низкого энергетических уровней.

На рис. 9.4. показаны возможные переходы и линии в спектре излучения двухатомной молекулы. Вращательные уровни не показаны.

Рис. 9.4. схема электронно–колебательных энергетических уровней и переходов молекул.

Вращательно–колебательно–электронные спектры излучения дают возможность рассчитать частоты колебания и коэффициенты ангармоничности в невозбужденном и электронно–возбужденном состоянии. Из рис. 9.4. видно, что разность энергий переходов 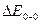и 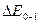равна разности энергии колебательных квантовых уровней с колебательными квантовыми числами 1 и 0, т.е.

.

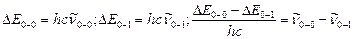Разность волновых чисел спектральных линий в спектре излучения равна волновому числу, соответствующему переходу молекулы с уровня 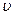=0 на уровень 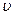=1, т.е. волновому числу основной полосы в колебательном спектре.

Разность энергий переходов и 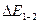соответствует энергии перехода с колебательного квантового уровня 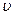=1 на колебательный квантовый уровень 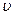=2.

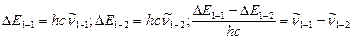
Сумма разностей волновых чисел линий излучения

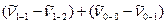
равна волновому числу первого обертона. На основании этих данных, используя уравнения (9.11), (9.12), можно вычислять частоту колебания 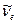и коэффициент ангармоничности 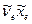. Аналогичный расчет дает возможность определить частоту колебания и коэффициент ангармоничности в электронно – возбужденном состоянии. Разность (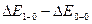) равна разности энергий на первом колебательном квантовом уровне и на нулевом колебательном квантовом уровне электронно – возбужденного состояния, т.е. позволяет определить волновое число основной полосы в электронно – возбужденном состоянии молекулы.

Разность 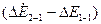сложенная с разностью (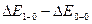) равна разности энергий уровней =2 и =0 в электронно–возбужденном состоянии. Это дает возможность определять 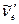и 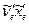. По частоте колебания и коэффициенту ангармоничности можно рассчитать энергию химической связи.

Если измерить среднее значение разности волновых чисел линий излучения, соответствующих переходам между вращательными уровнями, то возможно по уравнениям (9.6) и (9.8) определить момент инерции и межатомное расстояние.

Дата добавления: 2014-11-08