Основной закон динамики вращательного движения твердого тела относительно неподвижной оси

Момент инерции относительно оси вращения

Момент инерции материальной точки 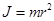, (1.8) где 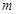– масса точки, 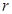– расстояние её от оси вращения.

1. Момент инерции дискретного твердого тела 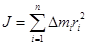, (1.9) где 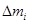– элемент массы твердого тела; 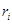– расстояние этого элемента от оси вращения; 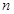– число элементов тела.

2. Момент инерции в случае непрерывного распределения массы (сплошного твердого тела) 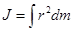. (1.10) Если тело однородно, т.е. его плотность 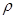одинакова по всему объему, то используется выражение 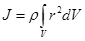(1.11), где 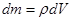и 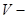объем тела.

3. Теорема Штейнера. Момент инерции тела 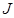любой оси вращения равен моменту его инерции 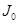относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы 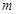тела на квадрат расстояния 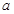между ними 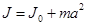. (1.12)

1. 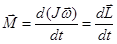, (1.13) где 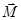– момент силы, 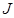– момент инерции тела, 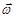– угловая скорость, 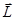– момент импульса.

2. В случае постоянного момента инерции тела – 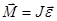, (1.14) где 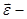угловое ускорение.

3. В случае постоянных момента силы 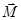и момента инерции изменение момента импульса 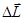вращающегося тела, равно произведению среднего момента сил, действующего на тело на время действия этого момента 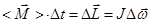. (1.15)

Если ось вращения не проходит через центр масс тела, то момент инерции тела относительно этой оси можно определить по теореме Штейнера: момент инерции тела 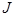относительно произвольной оси 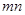равен сумме моментов инерции этого тела 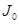относительно оси вращения О₁О_2, проходящей через центр масс тела С параллельно оси 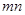, и произведения массы тела на квадрат расстояния между этими осями (см. Рис. 1), т.е. .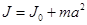

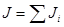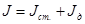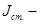Момент инерции системы отдельных тел равен (например, момент инерции физического маятника равен , где момент инерции стержня, на котором крепится диск с моментом инерции ).

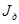Таблица аналогий

Поступательное движение	Вращательное движение
элементарное перемещение	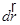элементарный заметённый угол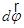
линейная скорость	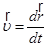угловая скорость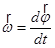
ускорение	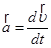угловое ускорение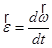
масса т	момент инерции J
сила	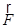момент силы
основное уравнение динамики поступательного движения	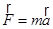основное уравнение динамики вращательного движения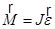
импульс	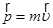момент импульса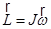
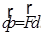
закон изменения импульса	закон изменения момента импульса
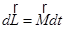
работа	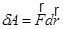работа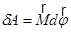
кинетическая энергия	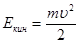кинетическая энергия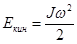

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения, момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.

Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю.

1)Еще линейными характеристиками: путь S, скорость,тангенциальноеи нормальное ускорения.

2)При вращении тела вокруг неподвижной оси вектор углового ускорения ε направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору ω (рис. 3), при замедленном - противонаправлен ему.

4) Момент инерции — скалярная величина, характеризующая распределение масс в теле. Момент инерции является мерой инертности тела при вращении (физический смысл).

Ускорение характеризует быстроту изменения скорости.

5) Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

6) Если груз подвешан и находится в покое,то сила упругости \натяжения\ нити по модулю равна силе тяжести.

Дата добавления: 2014-11-25