
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доведення
|
|
|
|
Дійсно,
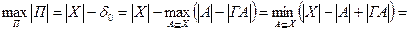
 .
.
5. Угорський алгоритм
З доказу теореми 1 безпосередньо випливає, що для побудови максимального паросполучення можна застосовувати алгоритм Форда - Фалкерсона. Розглянемо нижче інший шлях рішення цієї задачі, відомий за назвою угорського алгоритму. (Егевари, 1931 р.).
Визначення. Нехай 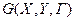 - простий граф і
- простий граф і 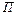 деяке його паросполучення. Дуги
деяке його паросполучення. Дуги 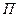 назвемо «жирними», інші дуги, «тонкими».
назвемо «жирними», інші дуги, «тонкими».
Визначення. Вершину графа назвемо насиченою, якщо вона інцидентна жирній дузі, у противному випадку - ненасиченою.
Визначення. Паросполучення назвемо повною, якщо кожна тонка дуга інцидентна хоча б одній насиченій вершині.
Визначення. Ланцюг, що з'єднує дві ненасичені вершини й складається з тонких і жирних дуг, що йдуть по черзі, назвемо ланцюгом, що чергується.

Рис. 11.3
На мал. 11.3 ланцюгом, що чергується, є, наприклад, 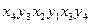 ланцюг, якщо
ланцюг, якщо  - жирні дуги.
- жирні дуги.
Угорський алгоритм полягає в наступному.
Крок 1. Побудувати довільне повне паросполучення 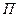 .
.
Крок 2. Якщо 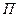 відображає всю множину
відображає всю множину 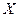 в
в 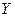 , то воно максимальне, алгоритм закінчений. Якщо ні, то перейти до кроку 3.
, то воно максимальне, алгоритм закінчений. Якщо ні, то перейти до кроку 3.
Крок 3. Знайти в графі 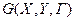 із установленим у ньому паросполучення
із установленим у ньому паросполучення 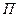 довільний ланцюг, що чергується,
довільний ланцюг, що чергується, 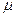 . Якщо такого ланцюга немає, то
. Якщо такого ланцюга немає, то 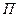 максимально, алгоритм закінчений. Якщо такий ланцюг є, то побудувати паросполучення
максимально, алгоритм закінчений. Якщо такий ланцюг є, то побудувати паросполучення 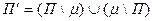 - паросполучення
- паросполучення 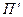 містить всі жирні дуги паросполучення
містить всі жирні дуги паросполучення 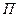 , що не входять у ланцюг
, що не входять у ланцюг 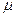 і всі тонкі дуги ланцюга
і всі тонкі дуги ланцюга 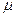 (див мал. 11.3 й 11.4). Перейти до кроку 2, поклавши
(див мал. 11.3 й 11.4). Перейти до кроку 2, поклавши 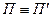 .
.

Рис. 11.4
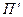 є паросполученням - це випливає з того, що включені в нього дуги ланцюга, що чергується,
є паросполученням - це випливає з того, що включені в нього дуги ланцюга, що чергується, 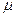 попарно несуміжні між собою й несуміжні з жирними дугами
попарно несуміжні між собою й несуміжні з жирними дугами 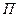 , що не належать
, що не належать 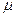 .
.
Так як число тонких дуг з ланцюга, що чергується, на 1 більше числа жирних, то  . Таким чином, кожен перехід від паросполучення
. Таким чином, кожен перехід від паросполучення 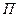 до паросполучення
до паросполучення 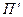 на кроці 3 збільшує кількість дуг. Залишається показати, що відсутність ланцюгів, що чергуються, означає максимальність паросполучення. Це буде зроблено пізніше в теоремі 6.
на кроці 3 збільшує кількість дуг. Залишається показати, що відсутність ланцюгів, що чергуються, означає максимальність паросполучення. Це буде зроблено пізніше в теоремі 6.
Для пошуку ланцюгів, що чергуються, на кроці 3 побудуємо допоміжний  граф. Його вершини відповідають дугам паросполучення
граф. Його вершини відповідають дугам паросполучення 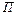 й однаково з ними позначаються. З вершини
й однаково з ними позначаються. З вершини 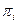 графа
графа  у вершину
у вершину 
 йде дуга, якщо в графі
йде дуга, якщо в графі 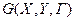 початок дуги
початок дуги 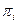 суміжний з кінцем дуги
суміжний з кінцем дуги  .(зокрема, у кожній вершині
.(зокрема, у кожній вершині 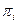 є петля). Для мал. 11.3 граф
є петля). Для мал. 11.3 граф  зображений на мал. 11.5.
зображений на мал. 11.5.

Рис. 11.5
Позначимо через 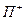 множину тих жирних дуг графа
множину тих жирних дуг графа 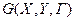 , кінці яких суміжні хоча б з однією його ненасиченою вершиною, а через
, кінці яких суміжні хоча б з однією його ненасиченою вершиною, а через  - множина жирних дуг, початок яких суміжний хоча б з однією ненасиченою вершиною. Наприклад, для графа на мал. 11.3 маємо
- множина жирних дуг, початок яких суміжний хоча б з однією ненасиченою вершиною. Наприклад, для графа на мал. 11.3 маємо  . У загальному випадку
. У загальному випадку  .
.
Кожному шляху на графі  від вершини, що належить множині
від вершини, що належить множині 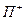 , до вершини, що належить множині
, до вершини, що належить множині 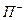 , відповідає ланцюг, що чергується, у вихідному графі. Дійсно, нехай у графі
, відповідає ланцюг, що чергується, у вихідному графі. Дійсно, нехай у графі  є шлях
є шлях  , у якому
, у якому  , а
, а 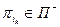 . Тоді в графі
. Тоді в графі 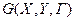 кінець жирної дуги
кінець жирної дуги 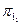 суміжний з деякою ненасиченою вершиною
суміжний з деякою ненасиченою вершиною  , її початок з кінцем жирної дуги
, її початок з кінцем жирної дуги  й т.д., початок жирної дуги
й т.д., початок жирної дуги 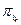 суміжно з деякою ненасиченою вершиною
суміжно з деякою ненасиченою вершиною  . Таким чином, вершини
. Таким чином, вершини 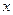 й
й  з'єднані ланцюгом, що чергується. Наприклад, шляхи
з'єднані ланцюгом, що чергується. Наприклад, шляхи  на мал. 11.5 відповідає ланцюг, що
на мал. 11.5 відповідає ланцюг, що 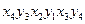 чергується, на мал. 11.1.
чергується, на мал. 11.1.
6. Обгрунтування угорського алгоритму
Метод ланцюгів, що чергуються, заснований на наступній теоремі.
Теорема 6. Наступні 4 умови еквівалентні:
1) у простому графі 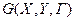 паросполучення
паросполучення 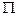 максимальне;
максимальне;
2) у простому графі 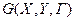 не існує ланцюгів, що чергуються;
не існує ланцюгів, що чергуються;
3) у графі 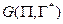 не існує шляху, що йде із вершини множини
не існує шляху, що йде із вершини множини 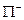 в вершину
в вершину
множини 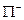 ;
;
4) у графі 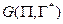 кожну вершину можна позначити знаком «+» або «-» так, щоб всі вершини множини
кожну вершину можна позначити знаком «+» або «-» так, щоб всі вершини множини 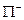 одержали знак «+», а всі вершини множини
одержали знак «+», а всі вершини множини  - знак «-» і щоб ніяка дуга не йшла з «+» в «-».
- знак «-» і щоб ніяка дуга не йшла з «+» в «-».
Доведення. Покажемо, що має місце наступний ланцюжок імплікацій  .
.
 . Справді, якби існував ланцюг, що чергується,
. Справді, якби існував ланцюг, що чергується, 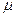 з'єднуючий дві різні ненасичені вершини, то по доведеному в попередньому пункті можна було б побудувати
з'єднуючий дві різні ненасичені вершини, то по доведеному в попередньому пункті можна було б побудувати  паросполучення, що має на одну дугу більше ніж,
паросполучення, що має на одну дугу більше ніж, 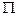 .
.
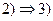 . Тому що по доведеному в попередньому пункті кожному шляху з
. Тому що по доведеному в попередньому пункті кожному шляху з 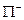 у
у 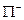 відповідає ланцюг, що чергується.
відповідає ланцюг, що чергується.
 . Позначимо знаком «+» всі вершини графа
. Позначимо знаком «+» всі вершини графа 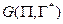 , що належать множині
, що належать множині  , тобто, які є кінцями шляхів, що виходять із вершин
, тобто, які є кінцями шляхів, що виходять із вершин 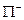 , і знаком «-» всі вершини множини
, і знаком «-» всі вершини множини  . При цьому умова 4 буде виконаною. Дійсно, кожна вершина графа
. При цьому умова 4 буде виконаною. Дійсно, кожна вершина графа 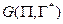 позначена. Вершини
позначена. Вершини 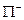 одержали знак «+», тому що
одержали знак «+», тому що  (у кожній вершині є петля). Вершини
(у кожній вершині є петля). Вершини 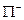 одержали знак «–», тому що за умовою 3
одержали знак «–», тому що за умовою 3 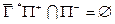 й, виходить,
й, виходить,  . При цьому по визначенню множин
. При цьому по визначенню множин  і
і  ніяка дуга не йде з «+» в «-».
ніяка дуга не йде з «+» в «-».
 . У графі
. У графі 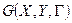 з паросполученням
з паросполученням 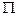 позначимо жирні дуги знаком «+» або «-» відповідно до умови 4 і позначимо через
позначимо жирні дуги знаком «+» або «-» відповідно до умови 4 і позначимо через  множину початкових вершин жирних дуг, позначених знайомий «-», а через
множину початкових вершин жирних дуг, позначених знайомий «-», а через 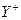 множину кінців жирних дуг, позначених знайомий «+».
множину кінців жирних дуг, позначених знайомий «+».
Для дуги  , що задовольняє умові
, що задовольняє умові 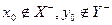 , розглянемо чотири випадки розташування (див. мал. 11.6).
, розглянемо чотири випадки розташування (див. мал. 11.6).
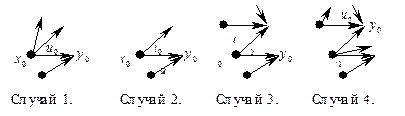
Рис. 11.6
Випадок 1. Вершини  й
й  ненасичені. Цей випадок неможливий, тому що
ненасичені. Цей випадок неможливий, тому що 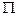 - повне паросполучення.
- повне паросполучення.
Випадок 2. Вершина  не насичена, вершина
не насичена, вершина  насичена. Тоді існує дуга
насичена. Тоді існує дуга  , інцидентна
, інцидентна  . Оскільки
. Оскільки 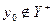 , дуга
, дуга 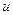 повинна бути позначена знайомий «-». Далі, вершина
повинна бути позначена знайомий «-». Далі, вершина  - кінець дуги
- кінець дуги 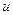 - суміжна з ненасиченою вершиною
- суміжна з ненасиченою вершиною  , тому
, тому 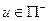 й
й 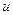 повинна бути позначена знайомий «+». Таким чином, і цей випадок неможливий.
повинна бути позначена знайомий «+». Таким чином, і цей випадок неможливий.
Випадок 3. Вершина  насичена, вершина
насичена, вершина  не насичена. Цей випадок розглядається також, як і попередній, і так само неможливий.
не насичена. Цей випадок розглядається також, як і попередній, і так само неможливий.
Випадок 4. Вершини  й
й  насичені. Розглянемо дуги
насичені. Розглянемо дуги 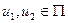 , перша з яких інцидентна
, перша з яких інцидентна  , друга
, друга  . Дуга
. Дуга  повинна бути позначена знайомий «+», дуга
повинна бути позначена знайомий «+», дуга 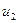 - знаком «-». Звідси, насамперед, треба, що
- знаком «-». Звідси, насамперед, треба, що  . Далі, тому що вершина
. Далі, тому що вершина  - кінець дуги
- кінець дуги 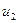 - суміжна з початком
- суміжна з початком  дуги
дуги  , позначеної знайомий «+», то
, позначеної знайомий «+», то  . Останнє суперечить умові 4, відповідно до якого жодна дуга не повинна йти з «+» в «-». Таким чином, і цей випадок неможливий.
. Останнє суперечить умові 4, відповідно до якого жодна дуга не повинна йти з «+» в «-». Таким чином, і цей випадок неможливий.
Тому що випадки 1 - 4 неможливі, то в кожної дуги  або
або  , тобто множина
, тобто множина 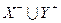 є опорою.
є опорою.
У силу теореми 5 для будь-якого паросполучення  й будь-якої опори
й будь-якої опори 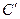 маємо
маємо  . У нашому випадку будь-яка дуга паросполучення
. У нашому випадку будь-яка дуга паросполучення 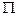 має тільки одну загальну вершину з опорою
має тільки одну загальну вершину з опорою  . Отже,
. Отже, 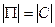 і паросполучення
і паросполучення 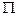 є найбільшим (а опора
є найбільшим (а опора 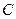 - найменшою).
- найменшою).
7. Внутрішньо стійкі множини простого графа
З визначення внутрішньо стійкої множини й угорського алгоритму випливає Т.7.
Теорема 7. Множина 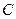 вершин простого графа
вершин простого графа 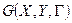 тоді й тільки тоді є його опорою, коли множина
тоді й тільки тоді є його опорою, коли множина 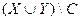 внутрішньо стійка.
внутрішньо стійка.
Для числа внутрішньої стійкості 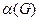 з Т. 7 слідує
з Т. 7 слідує
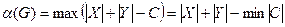 .
.
Звідси й з Т.5 випливає Т.8.
Теорема 8. Число внутрішньої стійкості простого графа 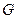
 дорівнює
дорівнює 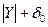 .
.
Для побудови найбільшого внутрішньо стійкої множини простого графа 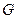 в силу Т. 7 можна скористатися одним з наведених алгоритмів побудови найбільшого паросполучення в графі
в силу Т. 7 можна скористатися одним з наведених алгоритмів побудови найбільшого паросполучення в графі 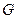 .
.
Відзначимо, що для довільного (не обов'язково простого) графа 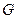 можна ввести паро сполуки, й з їхньою допомогою будувати його внутрішньо стійкі множини.
можна ввести паро сполуки, й з їхньою допомогою будувати його внутрішньо стійкі множини.
8. Питання для самоконтролю
1. Дати визначення дводольного графу.
2. Дати визначення паросполученню.
3. В чому полягає суть задачі про призначення.
4. Довести необхідність теореми про весілля.
5. Дати визначення трансверсалі.
6. Що називають дефіцитом простого графа.
7. Дати визначення опори простого графа. Яка опора називається найменшою?
8. В чому полягає суть Угорського алгоритму?
9. Які вершині називаються насиченими/ненасиченими?
10. Яке паросполучення називається повним?
11. На якій теоремі заснований метод ланцюгів? Сформулювати дану теорему.
12. Число внутрішньої стійкості простого графу. Дати визначення. Чому воно дорівнює?
13. Як побудувати найбільш внутрішньо стійку множину простого графа G?
Відповіді на запитання
1. Орієнтований граф 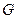 без кратних дуг називається простим або дводольним(двочастковим), якщо множина всіх його вершин можна представити у вигляді об'єднання двох множин (часток)
без кратних дуг називається простим або дводольним(двочастковим), якщо множина всіх його вершин можна представити у вигляді об'єднання двох множин (часток) 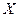 і
і 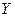 так, щоб дуги виходили тільки з вершин множини
так, щоб дуги виходили тільки з вершин множини 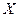 й заходили тільки у вершини множини
й заходили тільки у вершини множини 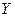 .
.
2. Паросполученням простого графа називається така підмножина 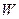 множини
множини  його дуг, у якому ніякі дві дуги з
його дуг, у якому ніякі дві дуги з 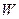 несуміжні (тобто не мають загальної вершини).
несуміжні (тобто не мають загальної вершини).
3. До цього зводиться, наприклад, що випливає задача про призначення. В керуванні трудових резервів є 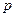 працівників
працівників  , що мають різні спеціальності. Потрібно їх призначити на
, що мають різні спеціальності. Потрібно їх призначити на  робочих місць
робочих місць 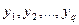 . Деякі із працівників мають (або можуть досить швидко придбати) не одну спеціальність. Чи можна їх розподілити так, щоб кожен працівник зайняв робоче місце у відповідності зі своєю спеціальністю? Цій задачі відповідає двочастковий граф, у якого з вершини
. Деякі із працівників мають (або можуть досить швидко придбати) не одну спеціальність. Чи можна їх розподілити так, щоб кожен працівник зайняв робоче місце у відповідності зі своєю спеціальністю? Цій задачі відповідає двочастковий граф, у якого з вершини 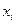 у вершину
у вершину 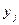 йде дуга, якщо працівник
йде дуга, якщо працівник 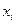 має спеціальність
має спеціальність 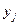 .
.
4. Теорема 1. Паросполучення простого графа 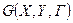 , що відображає все
, що відображає все 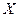 в
в 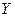 , існує тоді й тільки тоді, коли
, існує тоді й тільки тоді, коли  для будь-якої підмножини
для будь-якої підмножини 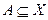 (нагадаємо, що
(нагадаємо, що 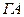 позначає множину всіх вершин графа
позначає множину всіх вершин графа 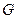 , у які заходять дуги, що виходять із вершин множини
, у які заходять дуги, що виходять із вершин множини  ,
, 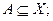
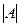 - позначає кількість вершин множини
- позначає кількість вершин множини  ).
).
|
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 663; Нарушение авторских прав?; Мы поможем в написании вашей работы!