
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коэффициент линейной корреляции
|
|
|
|
Тема 6 Линейная корреляция
Определение значимости корреляции
После вычисления коэффициента корреляции необходимо выдвинуть статистические гипотезы:
Н0: показатель корреляции значимо не отличается от нуля (является случайным).
Н1: показатель корреляции значимо отличается от нуля (является неслучайным).
Проверка гипотез осуществляется сравнением полученных эмпирических коэффициентов с табличными критическими значениями. Если эмпирическое значение достигает критического или превышает его, то нулевая гипотеза отвергается: rэмп ≥ rкр  Но, Þ Н1 . В таких случаях делают вывод, что обнаружена достоверность различий.
Но, Þ Н1 . В таких случаях делают вывод, что обнаружена достоверность различий.
Если эмпирическое значение не превышает критического, то нулевая гипотеза не отвергается: rэмп < rкр Þ Н0 . В таких случаях делают вывод, что достоверность различий не установлена.
Задания для самостоятельной работы.
1. Составить диаграмму корреляционной зависимости показателей субтестов «осведомленность» и «скрытые фигуры» (Таблица I) для первых 12 человек.
Коэффициент корреляции Пирсона называется также коэффициентом линейной корреляции или произведением моментов Пирсона. Он позволяет определить силу связи между двумя признаками, измеренными в метрических шкалах.
Его формула выглядит следующим образом:


У разных авторов эта формула может выглядеть по-разному. В данном пособии формула приводится в том виде, как она дана в кн. Наследов А.Д., Тарасов С. Г. «Применение математических методов в психологии».
Последовательность расчетов можно продемонстрировать на следующем примере. Итак, необходимо:
1. Вычислить значение корреляции между показателями роста в сантиметрах и веса в килограммах у представителей группы студентов.
2. Поставить вопрос о достоверности этого коэффициента. Для решения второй задачи необходимо предварительно сформулировать нулевую и альтернативную гипотезы:
Н0: корреляция между показателями роста и веса значимо не отличается от нуля (является случайной).
Н1: корреляция между показателями роста и веса значимо отличается от нуля (является неслучайной).
3. Данные заносятся в таблицу, при этом желательно, чтобы один из столбцов значений признака (показатели роста или веса) был упорядочен. 
| № | X (рост) | Y (вес) | xi-Мх | (xi-Мх)2 | yi-Му | (yi-Му)2 | (xi-Mx)*(yi-My) |
| -7,6 | 57,76 | -11,3 | 127,69 | 85,88 | |||
| -6,6 | 43,56 | -9,3 | 86,49 | 61,38 | |||
| 5,4 | 29,16 | 6,7 | 44,89 | 36,18 | |||
| -6,6 | 43,56 | -1,3 | 1,69 | 8,58 | |||
| 10,4 | 108,16 | 12,7 | 161,29 | 132,08 | |||
| -3,6 | 12,96 | -8,3 | 68,89 | 29,88 | |||
| -2,6 | 6,76 | 0,7 | 0,49 | -1,82 | |||
| -0,6 | 0,36 | 9,7 | 94,09 | -5,82 | |||
| 8,4 | 70,56 | 4,7 | 22,09 | 39,48 | |||
| 3,4 | 11,56 | -4,3 | 18,49 | -14,62 | |||
| n=10 | Мх=166,6 | Мy=58,3 | Σ=384,4 | Σ=626,1 | Σ=371,2 |
σх =  ≈ 6,53 σу =
≈ 6,53 σу = 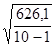 ≈ 8,34
≈ 8,34
Rxy =  ≈ 0,758
≈ 0,758
|
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 288; Нарушение авторских прав?; Мы поможем в написании вашей работы!