
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вектор-электрокардиография
|
|
|
|
Метод отведений Эйнтховена
Эйнтховен предложил при проведении электрокардиографии измерять разность потенциалов между каждыми двумя вершинами равностороннего треугольника, построенного симметрично относительно тела человека, а центр теугольника совпадает с точкой интегрального электрического вектора сердца. Вершины этого треугольника лежат на левом предплечье (ЛР), правом предплечье (ПР) и левой ноге (ЛН). На каждые две точки накладываются по электроду, и между ними измеряется разность потенциалов. Каждые две точки наложения электродов называются стандартными отведениями. 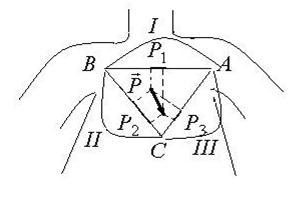
Отведения:
I – ЛР-ПР;
II – ЛН-ПР;
III- ЛН-ЛР.
Разности потенциалов между каждыми двумя точками пропорциональны проекциям дипольного момента на линию, соединяющую соответствующие точки:
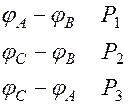
Точку приложения вектора 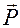 можно считать постоянной (точка, совпадающая с нервным узлом межпредсердной перегородки), а конец вектора
можно считать постоянной (точка, совпадающая с нервным узлом межпредсердной перегородки), а конец вектора 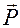 за цикл работы описывает сложную пространственную кривую. С помощью осциллографа, используя его усилители, можно наблюдать проекции этой пространственной кривой на фронтальную, горизонтальную и сагиттальную плоскости, совмещенные с телом обследуемого.
за цикл работы описывает сложную пространственную кривую. С помощью осциллографа, используя его усилители, можно наблюдать проекции этой пространственной кривой на фронтальную, горизонтальную и сагиттальную плоскости, совмещенные с телом обследуемого.
В плоскости при этом наблюдаются петли  , образованные сложением взаимноперпендикулярных колебаний мгновенных значений ЭКГ в двух каких-либо отведениях (фигуры Лиссажу)
, образованные сложением взаимноперпендикулярных колебаний мгновенных значений ЭКГ в двух каких-либо отведениях (фигуры Лиссажу) 
Этот метод называется вектор-электрокардтографией, а полученная кривая вектор- электрокардиограммой (ВЭКГ). Вектор-электрокардиограмма - кривая, показывающая геометрическое место точек, соответствующих положению конца вектора 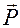 за время одного цикла.
за время одного цикла.
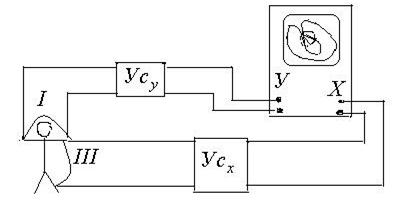
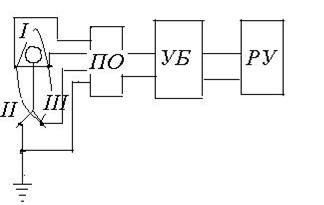
Блок-схема осциллографа.
Электрокардиограмма регистрируется на приборе, называемом электрокардиографом. Он содержит следующие основные блоки:
Лекция 10
ЭЛЕКТРОДИНАМИКА
Электрические колебания.
1. Процессы, происходящие в идеальном
колебательном контуре.
Электромагнитные колебания – колебания величин заряда, силы тока, напряжения, эдс индукции.
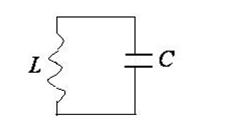
Электромагнитные колебания создаются в закрытом колебательном контуре, который представляет собой электрическую цепь, содержащую катушку индуктивности и конденсатор.
 Мы начнем с изучения свободных (собственных) колебаний, т.е. колебаний, которые совершаются без внешнего воздействия за счет первоначально накопленной энергии.
Мы начнем с изучения свободных (собственных) колебаний, т.е. колебаний, которые совершаются без внешнего воздействия за счет первоначально накопленной энергии.
Рассмотрим идеальный колебательный контур, т.е. контур, в котором активное сопротивление 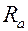 (сопротивление проводов катушки) равно нулю.
(сопротивление проводов катушки) равно нулю.
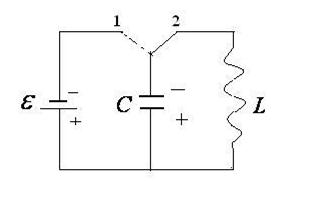
Если переведем ключ в положение 1, то конденсатор зарядится от источника тока так, что на его пластинах накопится максимальный заряд 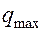 (на одной пластине +, на другой -). Перебросим ключ в положение 2 и? будем считать, что с этого момента времени
(на одной пластине +, на другой -). Перебросим ключ в положение 2 и? будем считать, что с этого момента времени  рассматриваем процессы, происходящие в контуре.
рассматриваем процессы, происходящие в контуре.
1. 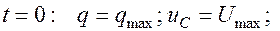 мгновенное значение тока
мгновенное значение тока 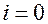 .
.
Будем рассматривать процесс в течение времени 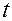 , равном одному периоду
, равном одному периоду 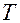 колебаний заряда на конденсаторе.
колебаний заряда на конденсаторе.
2. От 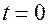 до
до 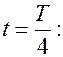 Конденсатор начинает разряжаться, заряд будет уменьшаться, стремясь к нулю. Напряжение на обкладках конденсатора
Конденсатор начинает разряжаться, заряд будет уменьшаться, стремясь к нулю. Напряжение на обкладках конденсатора 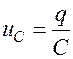 также будет уменьшаться. В контуре появится электрический ток
также будет уменьшаться. В контуре появится электрический ток 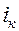 , который будет возрастать в этот промежуток времени. Проходя по катушке, возрастающий ток образует вокруг нее магнитное поле, которое будет возбуждать в катушке эдс самоиндукции. Эдс самоиндукции замедляет нарастание тока. Величина эдс определяется, как
, который будет возрастать в этот промежуток времени. Проходя по катушке, возрастающий ток образует вокруг нее магнитное поле, которое будет возбуждать в катушке эдс самоиндукции. Эдс самоиндукции замедляет нарастание тока. Величина эдс определяется, как 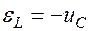 .
.
В момент времени 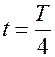 параметры контура:
параметры контура: 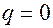 (конденсатор разрядился),
(конденсатор разрядился), 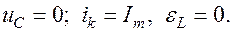
3. В промежуток времени от 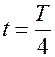 до
до 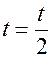 ток
ток 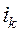 начинает убывать, в катушке возникает эдс индукции, замедляющая убывание тока. Под действием индукционного тока конденсатор перезаряжается – на пластинах появляется заряд противоположного знака. В момент времени
начинает убывать, в катушке возникает эдс индукции, замедляющая убывание тока. Под действием индукционного тока конденсатор перезаряжается – на пластинах появляется заряд противоположного знака. В момент времени 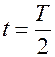 параметры контура:
параметры контура: 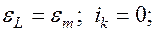
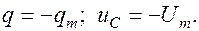
В промежутки времени от 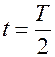 до
до 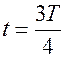 и от
и от 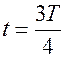 до
до 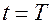
процесс повторяется в обратном направлении.
Таким образом, в колебательном контуре возникают электромагтиные колебания – колебания заряда, тока, напряжения и эдс индукции.
Рассмотрим теперь эти процессы строго, чтобы выяснить законы, по которым изменяются перечисленные величины.
Незатухающие электромагнитные колебания.
Такие колебания происходят в идеальном колебательном контуре, в котором 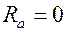 и не происходит потерь первоначально накопленной энергии на нагревание проводов. Эти колебания являются свободными.
и не происходит потерь первоначально накопленной энергии на нагревание проводов. Эти колебания являются свободными.
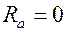
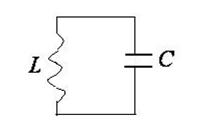
Согласно закону сохранения энергии для этой цепи следует записать
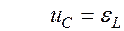
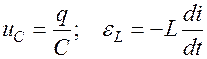 . Следовательно,
. Следовательно,
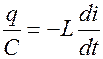 , перенесем
, перенесем 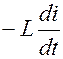 влево
влево 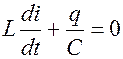 .
.
Т.к. 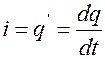 , то
, то 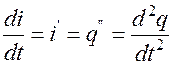 и уравнение запишется как
и уравнение запишется как
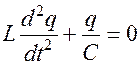 . Разделим обе части уравнения на
. Разделим обе части уравнения на 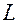 , получим
, получим
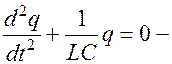 дифференциальное уравнение 2-го порядка для незатухающих электрических колебаний. Его решением является функция
дифференциальное уравнение 2-го порядка для незатухающих электрических колебаний. Его решением является функция
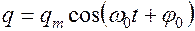
или 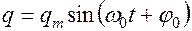 .
.
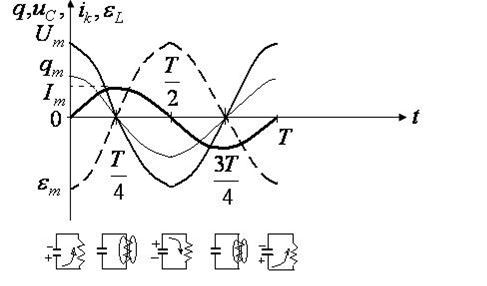
График этой функции:
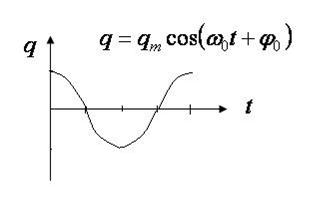
ННапряжение на конденсаторе рассчитаем по формуле 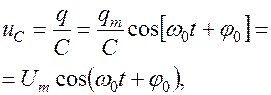 т.е. напряжение совпадает по фазе с зарядом.
т.е. напряжение совпадает по фазе с зарядом.
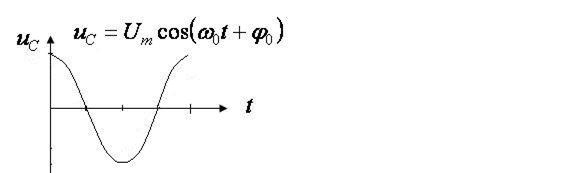
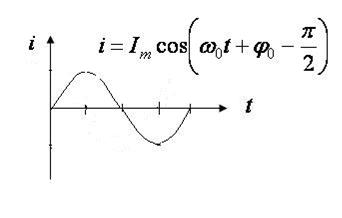 Ток в контуре
Ток в контуре
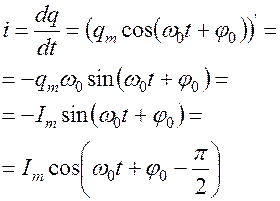
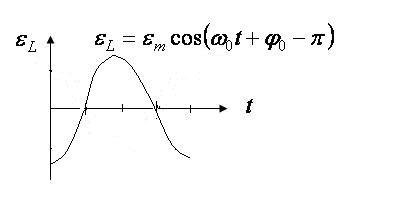 Эдс индукции
Эдс индукции 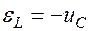 .
. 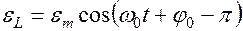 Находится в противофазе с зарядом и с напряжением на конденсаторе.
Находится в противофазе с зарядом и с напряжением на конденсаторе.
Период колебаний незатухающих колебаний определяется по формуле Томпсона: 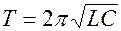 .
.
Затухающие колебания
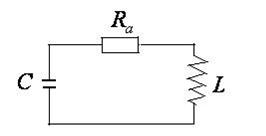 Рассмотрим свободные колебания в реальном колебательном контуре. В нём
Рассмотрим свободные колебания в реальном колебательном контуре. В нём 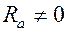 , следовательно, провода катушки будут нагреваться, энергия, первоначально накопленная энергия будет теряться. Такие колебания называются затухающими.
, следовательно, провода катушки будут нагреваться, энергия, первоначально накопленная энергия будет теряться. Такие колебания называются затухающими.
Согласно 2-ому правилу Кирхгофа сумма напряжений на элементах замкнутого контура равна сумме эдс, заключенных в этом контуре (следует из закона сохранения энергии): 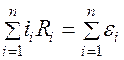 . Следовательно, для данного контура запишем:
. Следовательно, для данного контура запишем:
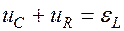 .
.
Т.к. 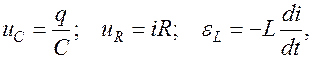 то это уравнение запишется как
то это уравнение запишется как
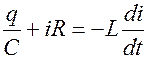 или
или
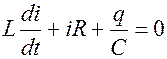 .
.
Разделим на 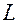 и, отметив, что
и, отметив, что 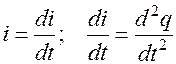 , получим
, получим
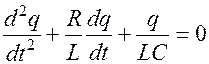 .
.
Введя обозначения: 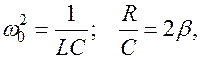 где
где 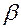 - коэффициент затухания, получим
- коэффициент затухания, получим
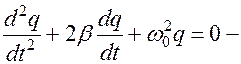
ДУ 2-го порядка для затухающих колебаний. Его решением является функция
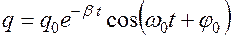 или
или
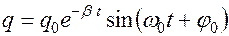 .
.
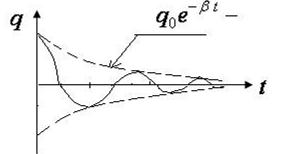
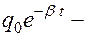 амплитуда затухающего колебания, убывает с течением времени по экспоненте. Само же колебание остаётся гармоническим. График затухающего колебания
амплитуда затухающего колебания, убывает с течением времени по экспоненте. Само же колебание остаётся гармоническим. График затухающего колебания
Напряжение на обкладках конденсатора изменяется по такому же закону, как и заряд, 
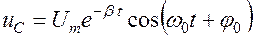 .
.
Сила тока в контуре
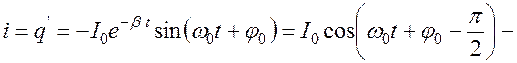 ток в контуре отстает от напряжения по фазе на
ток в контуре отстает от напряжения по фазе на 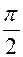 .
.
Быстрота затухания колебаний характеризуется логарифмически декрементом затухания
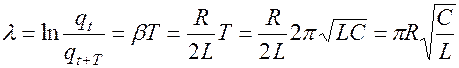 .
.
На практике удобнее использовать величину, называемую добротностью 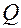 .
.
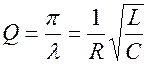 ,
,
т.е. быстрота затухания определяется параметрами контура.
Вынужденные колебания.
Чтобы колебания в контуре были не затухающими, к нему необходимо подать внешнюю эдс, которая должна быть периодической (изменяться по синусу или косинусу) и должна иметь частоту колебаний 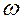 , отличную от частоты собственных колебаний:
, отличную от частоты собственных колебаний:
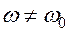 . Источник внешней эдс можно включать как параллельно, так и последовательно.
. Источник внешней эдс можно включать как параллельно, так и последовательно.
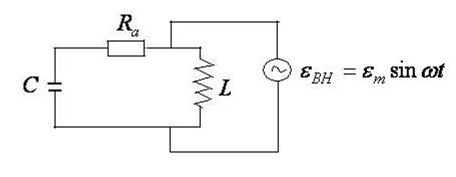
Тогда 2-ое правило Кирхгофа 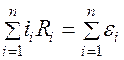 для такого контура
для такого контура
запишется в виде
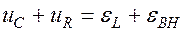 или
или
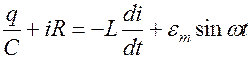
Производя замену 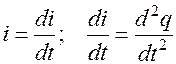 , деля на
, деля на 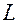 и введя обозначения
и введя обозначения 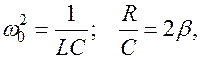 получим
получим
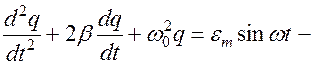
ДУ 2-го порядка для вынужденных колебаний. Решением этого уравнения является функция
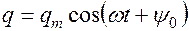 или
или
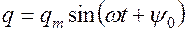 .
.
Анализируя это решение, находим, что колебания происходят с частотой внешней (вынуждающей) эдс. Начальная фаза колеба-
ний меняется на новую фазу 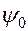 , Само же колебание остается гармоническим. И еще одна особенность: амплитуда вынужденных колебаний зависит от параметров источника внешней эдс
, Само же колебание остается гармоническим. И еще одна особенность: амплитуда вынужденных колебаний зависит от параметров источника внешней эдс
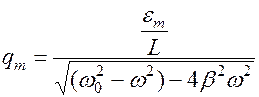 .
.
При малых затуханиях, т.е. при 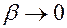
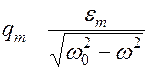 .
.
Если 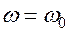 , то происходит резкое возрастание амплитуды заряда на пластинах конденсатора и напряжения. Это явление называется резонансом.
, то происходит резкое возрастание амплитуды заряда на пластинах конденсатора и напряжения. Это явление называется резонансом.
В практической медицине, например в аппарате для УВЧ - терапии вынужденные в контуре, содержащем основную нагрузку, поддерживаются с помощью эдс, возбуждаемой со стороны контура, составляющего часть генератора колебаний.
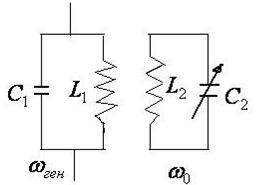
Эти два контура связаны индуктивной связью, а контур основной нагрузки имеет переменную ёмкость для настройки контуров в резонанс. Частота 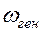 обычно задана, а
обычно задана, а 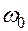 подбирается с помощью конденсатора
подбирается с помощью конденсатора 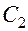 так, чтобы настроить эти контуры в резонанс. Поэтому в контуре
так, чтобы настроить эти контуры в резонанс. Поэтому в контуре 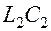 возникают колебания, резонансная кривая которых показана на рисунке
возникают колебания, резонансная кривая которых показана на рисунке
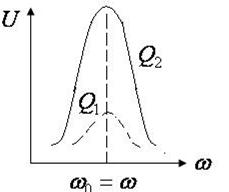 Острота кривой пропорциональна добротности контура.
Острота кривой пропорциональна добротности контура.
Автоколебания
см. лекцию “Механические колебания”.
Импульсные токи
Апериодический разряд конденсатора
Конденсатор – два проводника, разделенных диэлектриком, имеет ёмкость, имеет ёмкость, зависящую от размеров проводника и расстояния между ними.
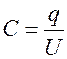
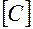 = 1 Ф (дольные единицы: 1 мкФ = 10-6 Ф, 1 пФ = 10-12 Ф)
= 1 Ф (дольные единицы: 1 мкФ = 10-6 Ф, 1 пФ = 10-12 Ф)
Ёмкость плоского конденсатора определяется по формуле 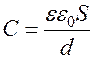 , где
, где 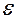 - диэлектрическая проницаемость диэлектрика,
- диэлектрическая проницаемость диэлектрика, 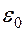 - электрическая постоянная,
- электрическая постоянная, 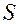 - площадь пластин,
- площадь пластин, 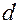 - расстояние между пластинами.
- расстояние между пластинами.
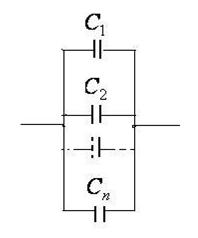
Конденсаторы включаются между собой последовательно
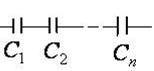 Общая емкость рассчитывается по формуле
Общая емкость рассчитывается по формуле 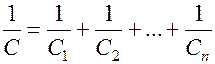
или параллельно:
Общая ёмкость: 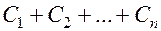
Апериодический разряд конденсатора
Если конденсатор подключить к генератору постоянного
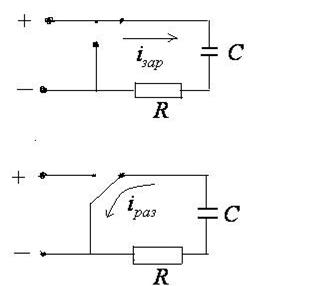 тока, электроны от отрицательного полюса генератора переходят на соединенную с ним пластину конденсатора, которая заряжается отрицательно. С другой пластины электроны переходят к положительному полюсу генератора, и она заряжается положительно. В диэлектрике между пластинами возникает электрическое поле. Этот процесс называется зарядкой конденсатора. Во внешней цепи появляется кратковременный импульс тока – ток зарядки конденсатора.
тока, электроны от отрицательного полюса генератора переходят на соединенную с ним пластину конденсатора, которая заряжается отрицательно. С другой пластины электроны переходят к положительному полюсу генератора, и она заряжается положительно. В диэлектрике между пластинами возникает электрическое поле. Этот процесс называется зарядкой конденсатора. Во внешней цепи появляется кратковременный импульс тока – ток зарядки конденсатора.
Если заряженный конденсатор отключить от источника напряжения и замкнуть его на сопротивление 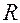 , то разность потенциалов
, то разность потенциалов 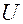 на его пластинах вызовет движение электронов во внешней цепи в направлении обратном первоначальному. В цепи образуется кратковременный импульс тока – ток разрядки конденсатора.
на его пластинах вызовет движение электронов во внешней цепи в направлении обратном первоначальному. В цепи образуется кратковременный импульс тока – ток разрядки конденсатора.
Чтобы выяснить форму и длительность импульсов тока при зарядке и разрядке конденсатора, рассмотрим простейший процесс – разрядки конденсатора.
Мгновенные значения тока разрядки по закону Ома
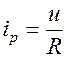 .
.
Т.к. 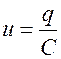 , то
, то

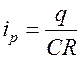 .
.
При 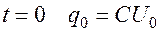 .
.
В этих формулах: 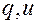 - мгновенные значения заряда и напряжения.
- мгновенные значения заряда и напряжения.
По определению
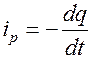 .
.
Знак “-“ означает, что ток возникает за счет убыли заряда. Очевидно, что можно записать
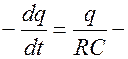 дифференциальное уравнение
дифференциальное уравнение
с разделяющимися переменными. Откуда
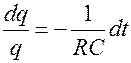 .
.
Интегрируя при условии, что при 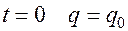 при
при 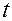 заряд равен
заряд равен 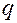 , получаем
, получаем
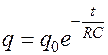
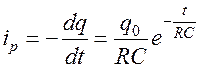
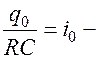 сила тока при
сила тока при 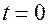 . Поэтому
. Поэтому
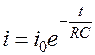 .
.
Аналогично изменяется и напряжение на обкладках конденсатора.
Графики тока разрядки и напряжения.
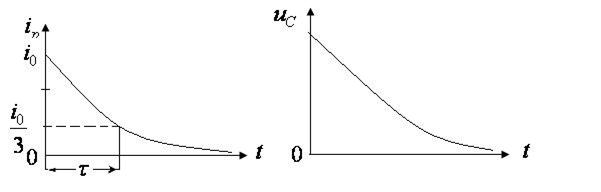
Экспоненциальная зависимость и форма импульса тока делает неопределенной его длительность. При физиологических исследованиях и в практической медицине на объект оказывает влияние только начальная часть импульса с относительно высокими значениями тока. За длительность импульса условно принимается время 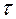 , такое, что ток уменьшается за это время до
, такое, что ток уменьшается за это время до 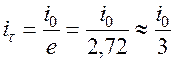 . Время
. Время 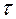 называется постоянной времени разрядки конденсатора.
называется постоянной времени разрядки конденсатора.
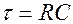
Ток зарядки имеет такую же форму, но течет в противоположном направлении.
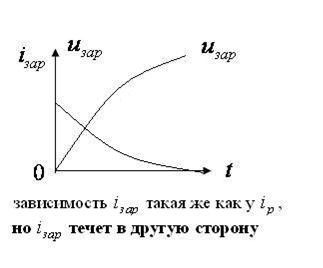
Таким образом, импульсы – это кратковременные изменения силы тока и напряжения.
Импульсный ток – это повторяющиеся во времени импульсы. Они могут быть самой различной формы:
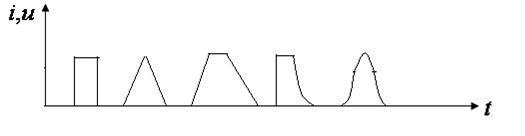
Характеристики импульсных токов.
1. Длительность импульса.
У реальных импульсов время начала, вершины и конца импульса размыты, поэтому экспериментальное определение этих величин может внести существенную ошибку. Для уменьшения возможной погрешности условились выделять моменты времени, при которых напряжение имеют значения 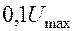 - начало и конец импульса и
- начало и конец импульса и 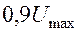 , где
, где 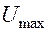 - амплитуда, т.е. наибольшее значение напряжения.
- амплитуда, т.е. наибольшее значение напряжения.
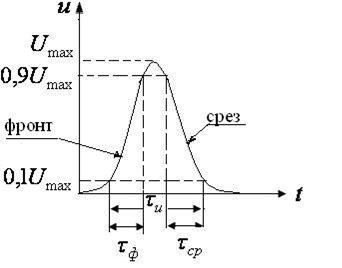
Таким образом, за длительность импульса принимается время, при котором напряжение (или сила тока) не меньше 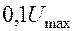 .
.
2. Крутизна фронта характеризует скорость нарастания напряжения или силы тока
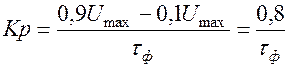 .
.
3. Период Т характеризует период повторения импульсов – это среднее время между началами двух соседних импульсов.
4. Частота повторения импульсов
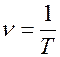
5. Скважность следования импульсов
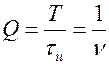
6. Коэффициент заполнения
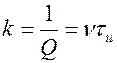
Генераторы импульсных токов.
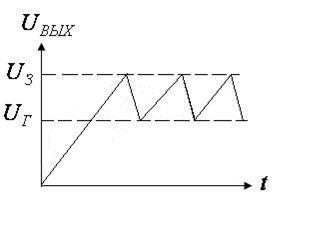
1. Генератор на неоновой лампе
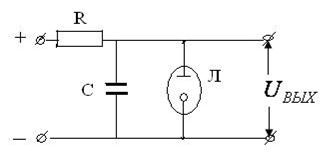
Неоновая лампа зажигается при строго определенном напряжении 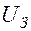 , а гаснет при меньшем напряжении
, а гаснет при меньшем напряжении 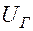 .
.
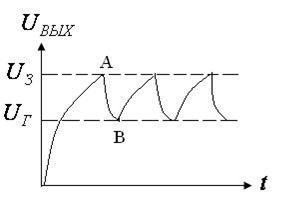
При включении генератора конденсатор заряжается до напряжения 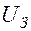 (на графике напряжений т.А). Газ в лампе ионизируется, лампа зажигается, и конденсатор разряжается через неё до напряжения
(на графике напряжений т.А). Газ в лампе ионизируется, лампа зажигается, и конденсатор разряжается через неё до напряжения 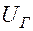 (т.В). Конденсатор опять подзаряжается, и процесс повторяется.
(т.В). Конденсатор опять подзаряжается, и процесс повторяется.
Т.к. 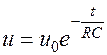 , то скорость нарастания напряжения можно изменять, меняя
, то скорость нарастания напряжения можно изменять, меняя 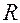 и
и 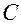 , можно так подобрать эти параметры, что напряжение будет пилообразным:
, можно так подобрать эти параметры, что напряжение будет пилообразным:
2. Блокинг-генератор
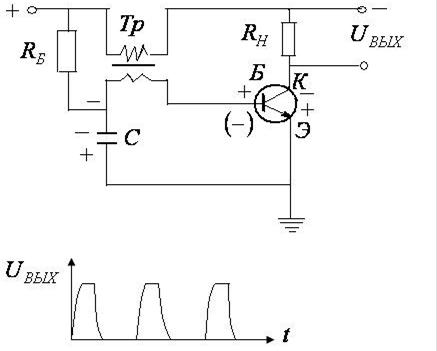
В начальный момент положительное напряжение на базе транзистора создается за счет базового тока от источника питания через резистор 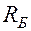 . В последующий момент через транзистор проходит импульс коллекторного тока, который поддерживается эдс индукции в трансформаторе. При этом конденсатор
. В последующий момент через транзистор проходит импульс коллекторного тока, который поддерживается эдс индукции в трансформаторе. При этом конденсатор 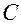 заряжается. Пока конденсатор заряжается, на базе создается отрицательный потенциал, и ток через транзистор не идет (транзистор заперт). Наступает пауза, в течение которой конденсатор разряжается через резистор
заряжается. Пока конденсатор заряжается, на базе создается отрицательный потенциал, и ток через транзистор не идет (транзистор заперт). Наступает пауза, в течение которой конденсатор разряжается через резистор 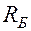 и источник тока. В результате разряда конденсатора база транзистора снова получает положительный потенциал через
и источник тока. В результате разряда конденсатора база транзистора снова получает положительный потенциал через 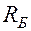 от источника тока, и процесс повторяется.
от источника тока, и процесс повторяется.
3. Мультивибратор
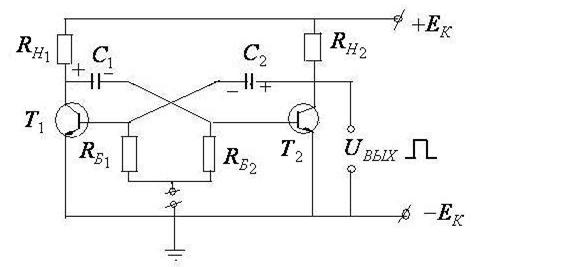
Мультивибратор содержит два конденсатора, два транзистора, два конденсатора и по паре сопротивлений  и
и  .
.
Конденсаторы служат для генерации импульсов (заряжаются от источника постоянного тока  и сопротивления
и сопротивления 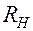 , а разряжаются через сопротивления
, а разряжаются через сопротивления 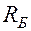 ). Транзисторы играют роль “включателей”. Симметричное их расположение в схеме обеспечивает поочередную зарядку конденсаторов: если открыт транзистор
). Транзисторы играют роль “включателей”. Симметричное их расположение в схеме обеспечивает поочередную зарядку конденсаторов: если открыт транзистор 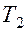 , то заряжается конденсатор
, то заряжается конденсатор 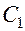 , если открыт транзистор
, если открыт транзистор 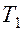 , то заряжается конденсатор
, то заряжается конденсатор 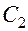 . Выходное напряжение
. Выходное напряжение 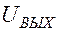
имеет прямоугольную форму.
Изменение формы импульса.
После мультивибратора получаются импульсы прямоугольной формы. Но для лечения различных заболеваний используют импульсы различной формы. Чтобы изменить форму импульса, на выходе мультивибратора собирают дифференцирующую или интегрирующую цепь:
1. Дифференцирующая цепь
Её применяют в том случае, если 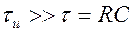 .
. 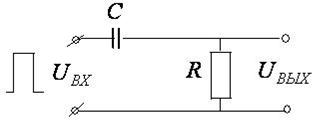
На вход цепочки подается входное напряжение прямоугольной формы.
Очевидно,
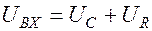 .
.
Выходное напряжение включено параллельно резистору 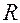 . Поэтому
. Поэтому
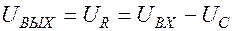 .
.
Форму выходного напряжения можно получить при графическом вычитании.
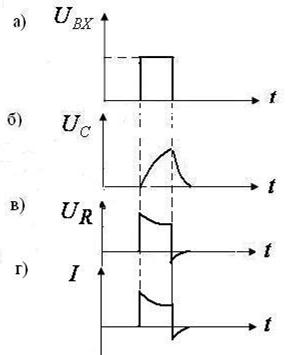
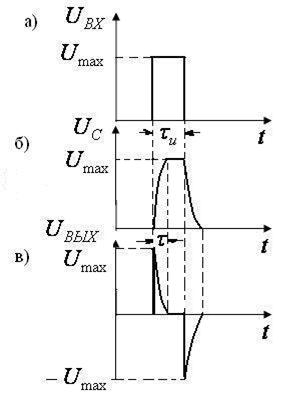 На рис. а) показан импульс входного напряжения. При вклю-чении цепочки конденсатор заряжается в течение времени
На рис. а) показан импульс входного напряжения. При вклю-чении цепочки конденсатор заряжается в течение времени 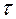 . В течение времени
. В течение времени 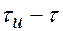 напряжение на конденсаторе остается постоянным. Затем импульс прекращается, конденсатор разряжается (рис. б). Вычитая значения функции, представленной на рис.б из значений функции, представленной на рис.а, получаем вид функции выходного напряжения (рис. в). Т.о. на выходе из цепочки получаются два кратковременных остроконечных импульса противоположного знака.
напряжение на конденсаторе остается постоянным. Затем импульс прекращается, конденсатор разряжается (рис. б). Вычитая значения функции, представленной на рис.б из значений функции, представленной на рис.а, получаем вид функции выходного напряжения (рис. в). Т.о. на выходе из цепочки получаются два кратковременных остроконечных импульса противоположного знака.
Рассмотренная цепочка называется дифференцирующей по-
тому, что выходное напряжение пропорционально производной от входного напряжения 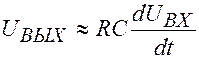 .
.
2. Интегрирующая цепь.
Применяется в том случае, если 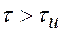 .
.
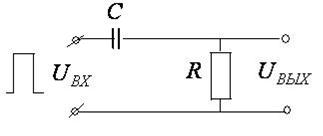 Выходное напряжение включено параллельно конденсатору
Выходное напряжение включено параллельно конденсатору 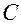 . Поэтому
. Поэтому
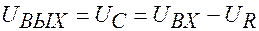 .
.
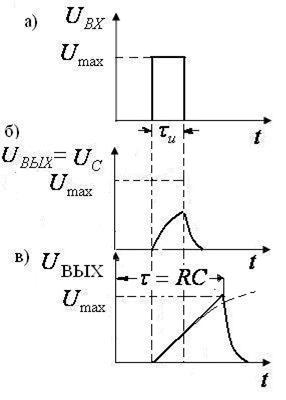 Если на вход цепи подан прямоугольный импульс (рис. а), то напряжением на выходе является напряжение на пластинах конденсатора, которое при зарядке имеет экспоненциально нарастающую и при зарядке экспоненциально спадающую форму (рис.б). Конденсатор не успевает зарядиться до
Если на вход цепи подан прямоугольный импульс (рис. а), то напряжением на выходе является напряжение на пластинах конденсатора, которое при зарядке имеет экспоненциально нарастающую и при зарядке экспоненциально спадающую форму (рис.б). Конденсатор не успевает зарядиться до 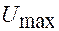 , т.к. на резисторе
, т.к. на резисторе 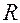 происходит падение напряжения, во-первых, и, во-вторых,
происходит падение напряжения, во-первых, и, во-вторых, 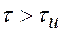 . Такие импульсы применяются при электростимуляции. При достаточно большой постоянной времени нарастание выходного импульса происходит по начальной части экспоненты (пунктирная линия), которая приближается к прямой линии - касательной к кривой в начальной точке. Этот случай называется идеальным интегрированием.
. Такие импульсы применяются при электростимуляции. При достаточно большой постоянной времени нарастание выходного импульса происходит по начальной части экспоненты (пунктирная линия), которая приближается к прямой линии - касательной к кривой в начальной точке. Этот случай называется идеальным интегрированием.
Рассмотренная цепочка называется интегрирующей потому, что выходное напряжение пропорционально интегралу 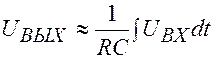 .
.
Действие импульсного тока на ткани организма
В основе действия электрического тока на ткани организма лежит движение электрически заряженных частиц, преимущественно ионов тканевых электролитов, в результате чего изменяется обычный состав ионов по обе стороны мембраны, в связи, с чем в клетке происходит ряд биофизических и физиологических процессов, вызывающих её возбуждение.
Постоянный ток почти не оказывает раздражающего действия на ткани организма. Раздражение вызывается при изменении силы тока и зависит от скорости, с которой это изменение происходит. Это положение известно как закон Дюбуа-Реймона. Сила тока 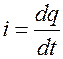 в растворе электролита зависит как от числа движущихся ионов, так и от скорости их перемещения. Скорость изменения силы тока
в растворе электролита зависит как от числа движущихся ионов, так и от скорости их перемещения. Скорость изменения силы тока 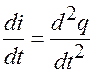 соответствует ускорению движения ионов. Поэтому можно считать, что раздражающее действие импульсного тока обусловлено ускорением при перемещении ионов тканевых электролитов.
соответствует ускорению движения ионов. Поэтому можно считать, что раздражающее действие импульсного тока обусловлено ускорением при перемещении ионов тканевых электролитов.
Очевидно, что раздражающее действие зависит от крутизны импульсов. Применяются одиночные импульсы, посылки (серии), определенного числа импульсов, а также импульсы, повторяющиеся ритмически с определенной частотой.
| Формы импульсных токов | Применение |
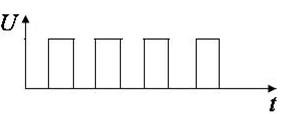 ПРЯМОУГОЛЬНЫЕ
ПРЯМОУГОЛЬНЫЕ
| 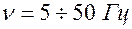 - электросон - электросон
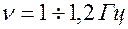 - электрокардиостимуляция - электрокардиостимуляция
|
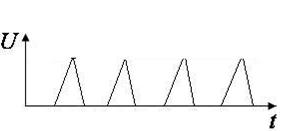 ТРЕУГОЛЬНЫЕ
ТРЕУГОЛЬНЫЕ
| 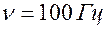 - возбуждение мышц, электрогимнастика - возбуждение мышц, электрогимнастика
|
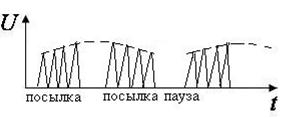 ТЕТАНИЗИРУЮЩИЕ
ТЕТАНИЗИРУЮЩИЕ
| 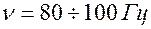 - электростимуляция здоровых мышц - электростимуляция здоровых мышц
|
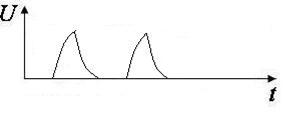 ЭКСПОНЕНЦИАЛЬНЫЕ
ЭКСПОНЕНЦИАЛЬНЫЕ
| 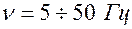 - электростимуляция - электростимуляция
|
 ЭКСПОНЕНЦИАЛЬНЫЕ
ЭКСПОНЕНЦИАЛЬНЫЕ
| Электростимуляция пораженных мышц |
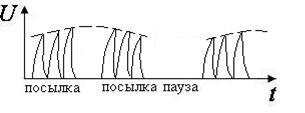
 ДИАДИНАМИЧЕСКИЕ
ДИАДИНАМИЧЕСКИЕ
| Электротерапия |
При физиологических исследованиях емкостные свойства тканей приводят к тому, что на емкости происходит падение напряжения (рис.б). Следовательно, напряжение на ткани станет по форме таким, как показано на рис.в) (график получен сложением  и
и 
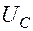 ). Следовательно, по ткани будет идти ток по форме аналогичный напряжению
). Следовательно, по ткани будет идти ток по форме аналогичный напряжению 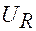 . Раздражающее действие прямоугольных импульсов в значительной мере зависит от их длительности
. Раздражающее действие прямоугольных импульсов в значительной мере зависит от их длительности 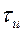 , обусловливающей наибольшее смещение ионов за время действия импульса. Эта зависимость описывается уравнением Вейса-Лапика
, обусловливающей наибольшее смещение ионов за время действия импульса. Эта зависимость описывается уравнением Вейса-Лапика
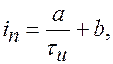
где 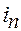 - пороговая сила тока (амплитуда импульса),
- пороговая сила тока (амплитуда импульса), 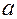 и
и 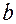 - коэффициенты, зависящие от природы возбуждаемой ткани и её функционального состояния. Зависимость
- коэффициенты, зависящие от природы возбуждаемой ткани и её функционального состояния. Зависимость 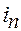 от
от 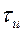 показана на рисунке:
показана на рисунке:
При достаточно длительных импульсах 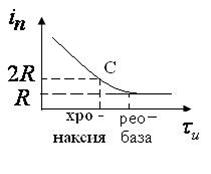 (правая ветвь кривой) раздражающее действие становится независимым от длительности (
(правая ветвь кривой) раздражающее действие становится независимым от длительности (
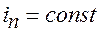 ). Значение порогового тока при этом называют реобазой
). Значение порогового тока при этом называют реобазой 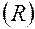 . Точка
. Точка 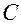 кривой, ордината которой равна удвоенной реобазе, определяет длительность импульса и называется хронаксией. Хронаксия и реобаза характеризуют возбудимость органа и могут служить показателями их функционального состояния или диагностического признака их поражения.
кривой, ордината которой равна удвоенной реобазе, определяет длительность импульса и называется хронаксией. Хронаксия и реобаза характеризуют возбудимость органа и могут служить показателями их функционального состояния или диагностического признака их поражения.
Лекция 11
Импеданс тканей организма.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 2642; Нарушение авторских прав?; Мы поможем в написании вашей работы!