Введение. Информационный менеджмент

Е.Т. Кожагулов, М.К. Ибраимов, С.А. Хохлов, Е.Сагидолда, Д.М. Жексебай

Информационный менеджмент

Составители Лапшина Светлана Николаевна

Ташлыков Владимир Викторович

Редактор _________________

_____________________________________________________________________________________

Подписано в печать _________ Формат 60´84 1/16

Бумага типографская Офсетная печать Усл. печ. л. 2,88

Уч.-изд. Л. 3,73 Тираж Заказ Цена «С»

____________________________________________________________________________________

Редакционно-издательский отдел ГОУ ВПО УГТУ-УПИ

620002, Екатеринбург, Мира, 19

Казахский национальный университет им. аль-Фараби, Алматы, Казахстан, [e-mail]

Генераторы динамического хаоса на программируемых логических интегральных схемах

Приведены результаты использования нового метода реализации хаотических генераторов на основе дифференциальных уравнений и отображении динамических систем. Цифровая схемотехника выполнена с помощью интегральных схем типа Field Programmable Gate Array. Показана возможность применения предлагаемого комплекса цифровой электронной техники для получения сверхширокополосных, сверхвысокочастотных, хаотических сигналов с разнообразными статистическими свойствами.

Ключевые слова: хаотический генератор, динамические системы, FPGA, информационные технологии, цифровые схемы.

К хаотизации движений в детерминированных нелинейных системах проявляется большой интерес, о чем свидетельствует нарастающий поток научной информации. Это связано множеством прикладных решений с применением различных генераторов хаотических сигналов, таких как расширение полосы спектра сигнала, конфиденциальная приемо-передача информационного сигнала и др. Для реализации таких задач мы выбрали программируемые логические интегральные схемы (ПЛИС), что повышает быстродействие генераторов за счет параллельной обработки данных.

Программируемые устройства представляют собой класс микросхем общего назначения, которые могут быть сконфигурованы для самых разнообразных применений. Встает естественный вопрос об отличии и преимущества использования ПЛИС относительно аналоговой схемотехники. В случае аналоговых хаотических генераторов есть проблема синхронизации приемника с передатчиком. Это требует согласования параметров как приемника так и передатчика с высокой степенью точности. Данное требование трудно достичь в аналоговых системах, так как компоненты аналогового контура являются функциями времени и температуры. Поэтому очевидной возможностью является использование цифровых приборов. С целью поиска методов моделирования сложных динамических систем, описываемых, например, дробными показателями степени [1].

Результаты численного анализа и сопоставление с физическими экспериментами. В качестве объектов исследований мы выбрали известные динамические системы, описываемые нелинейными дифференциальными уравнениями, или, отображениями. Для получения численных и графических данных использовался программный пакет MATLAB Simulink. Для примера ниже приведена структурная схема на цифровых логических элементах отображения Хенона:

x_i+1 = y_i + 1 – ax_i², y_i+1 = bx_i. (1)

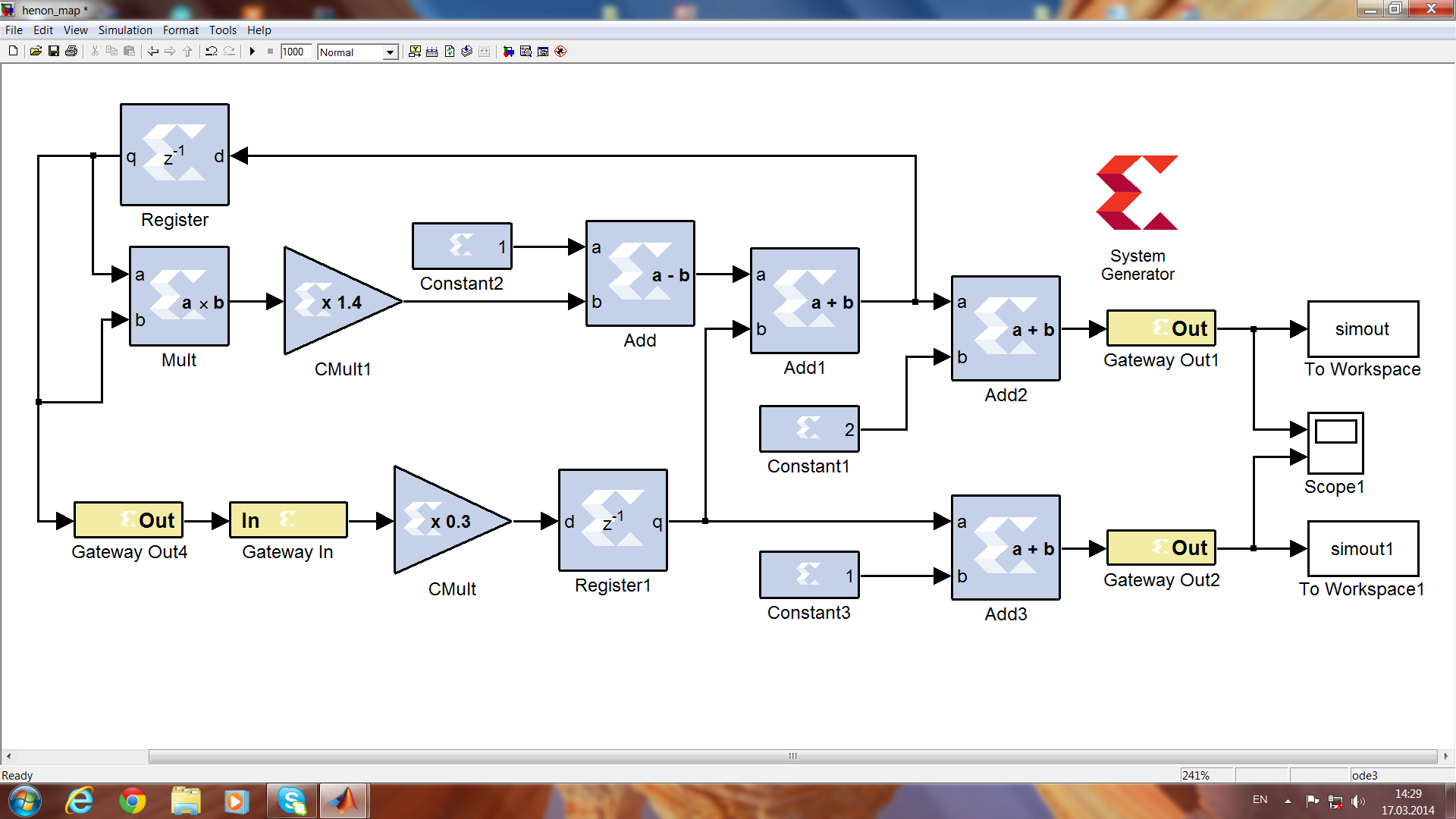
Рисунок 1. Структурная схема отображения Хенона с параметрами a=1.4, b=0.3.

Аппаратная часть реализована на основе отладочной платы DE FPGA BOARD c интегральной схемой фирмы XILINX семейства Spartan 3E(рис.2). Цифровой сигнал на выходе ПЛИС получен в виде восьми битного кода данных. На макетной плате собрана схема ЦАП для отображения аналоговых данных на осциллографе.

Рисунок 2. Отладочная плата DE FPGA BOARD

Подробная блок схема записанного программного кода в ПЛИС приведена на рисунке 3. Каждый блок выполняет определенные функции созданного алгоритма: первый блок выполняет деление частоты такта, второй обобщенный блок выдает сигнал по отображению Хенона.

Обратная связь

Рисунок 3. RTL схема отображения Хенона в ПЛИС.

Также на программном языке Verilog HDL осуществили обратную связь(рис.3). Эта линия соответствует линии между Gateway Out 4 и Gateway In в структурной схеме отображения Хенона на рисунке 1.

Экспериментальные результаты на основе ПЛИС и данные полученные численным методом отображения Хенона, логистического отображения, систем Росслера, Чуа и Лоренца [2-5] сопоставлены ниже.

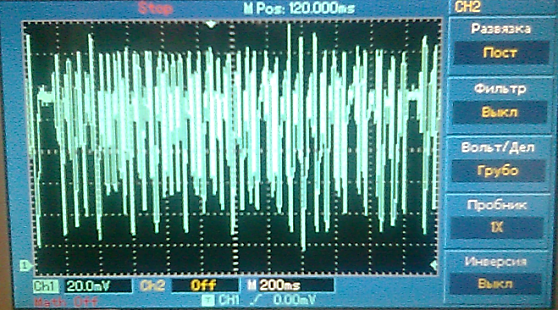
(a) (b)

(c) (d)

Рисунок 4. Численные реализации (а,c) и экспериментальные результаты (b,d) отображения Хенона (a,b); логистического отображения (c,d)

Динамические системы использованы в виде:

Система Росслера:

ẋ = – (y + z),

ẏ = x + αy,

ż = β + z(x – γ).

(a) (b)

Рисунок 5. Численные реализации (а) и экспериментальные результаты (b) системы Росслера, при α = 0.2, β = 0.2, γ = 5.7;

Система Чуа:

ẋ = kα(y – x – g(x)),

ẏ = k(x – y + z),

ż = k(– βy – γz),

g(x) = m₀x +0.5(m₁ − m₀)(|x + 1| − |x − 1|).

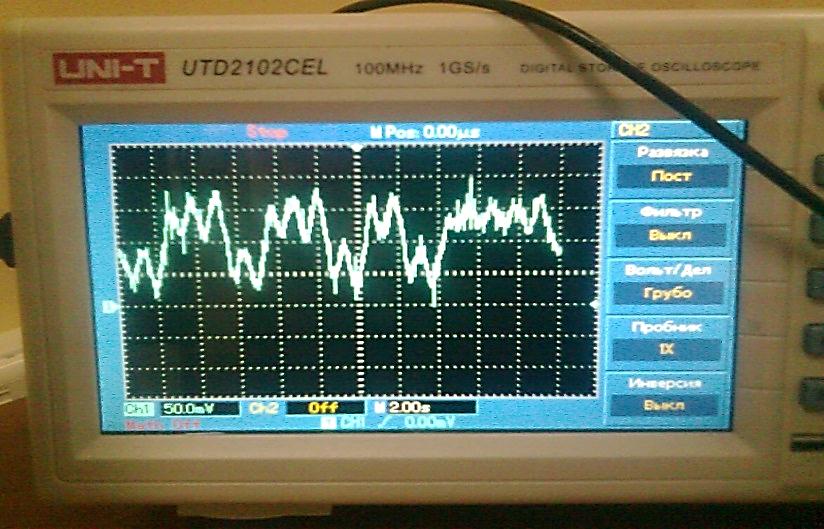
(a) (b)

Рисунок 6. Численные реализации (а) и экспериментальные результаты (b) системы Чуа,

при α = 6.579, k = 1, β = 10.897, m₀ = -0.652, m₁ = -1.812, γ = -0.045;

Система Лоренца:

ẋ = a(y – x),

ẏ = bx – y – xz,

ż = xy – cz, где a = 10, b = 28, c = 8/3.

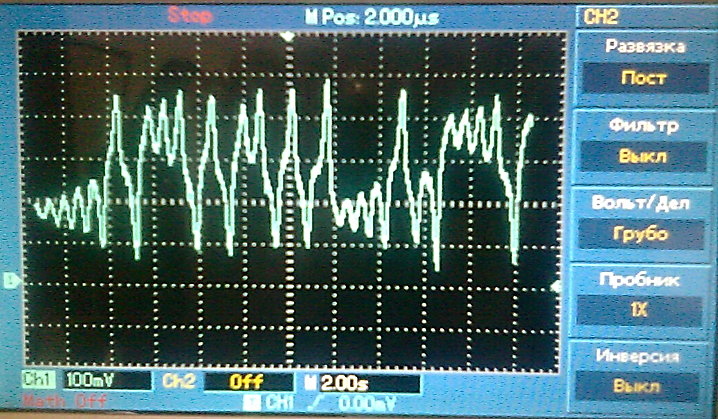
(a) (b)

Рисунок 7. Численные реализации (а) и экспериментальные результаты (b) системы Лоренца.

Ниже приведена структурная схема на цифровых логических элементах генератора динамического хаоса с фазовым управлением:

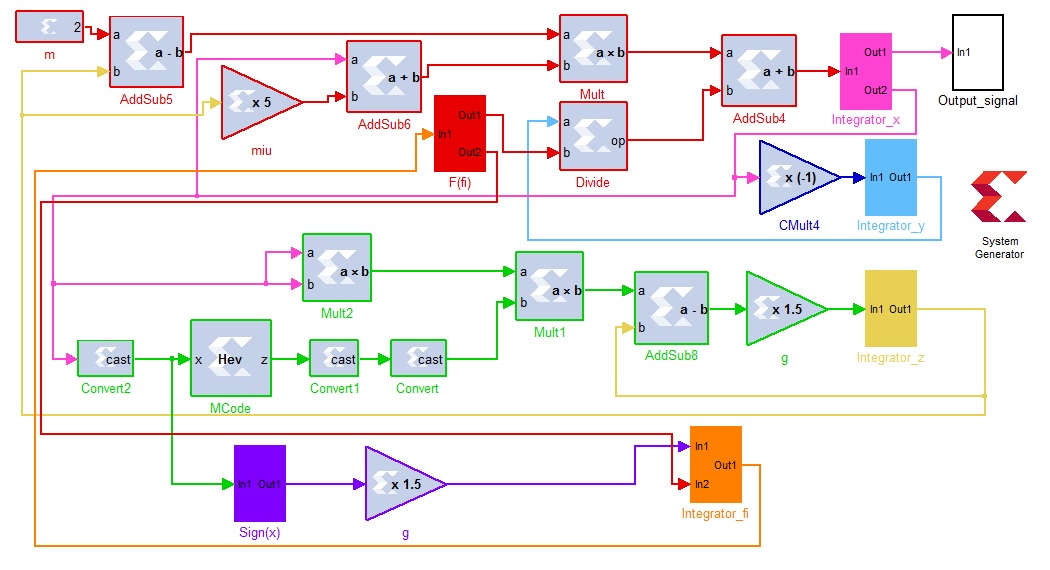
Рисунок 8. Структурная схема генератора динамического хаоса с фазовым управлением с параметрами A=0.95, m=2, μ=5, g=1.5.

Блок схема интегратора приведена на рисунке 9. Программа блок схемы Hev приведена на рисунке 10.

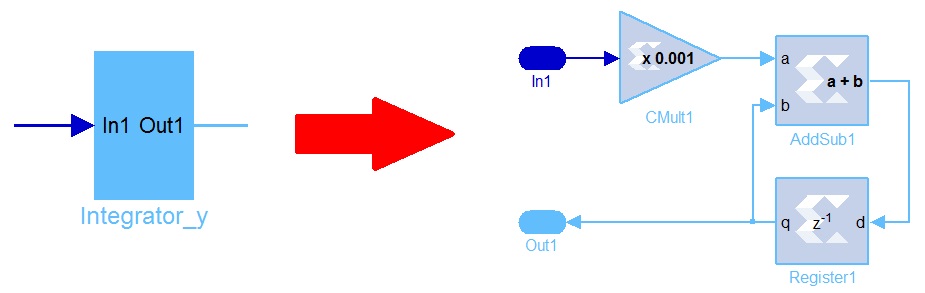
Рисунок 9. Блок схема интегратора.

Рисунок 10. Программа блок схемы Hev.

Ниже приведены блок схемы функции Sign(x) и F(φ), согласно рисунок 11 и рисунок 12.

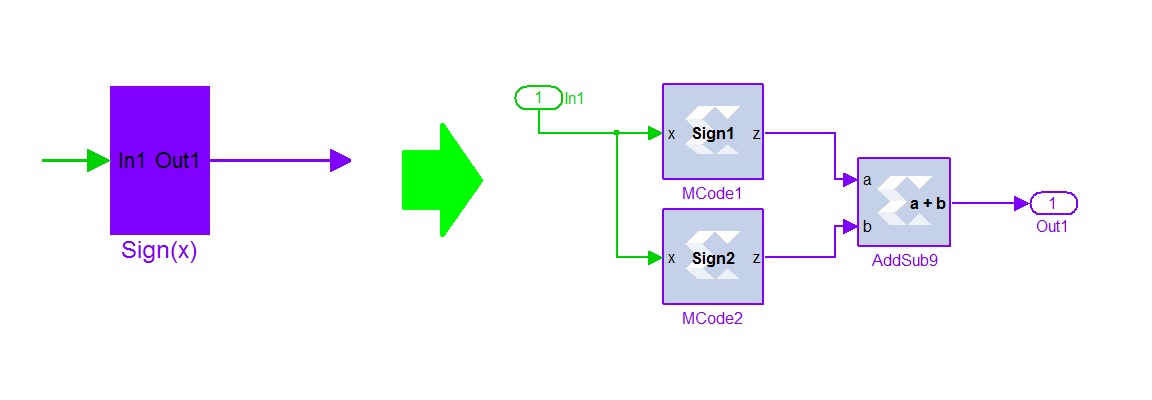Рисунок 11. Блок схема функции Sign(x).

Рисунок 12. Блок схема функции F(φ).

Аппаратная часть реализована на основе отладочной платы ANVYL FPGA c интегральной схемой фирмы XILINX семейства Spartan 6(рис.13). На макетной плате собрана схема ЦАП для отображения аналоговых данных на осциллографе.

Рисунок 13. Отладочная плата ANVYL FPGA.

RTL схема записанного программного кода в ПЛИС приведена на рисунке 14.

Рисунок 14. RTL схема генератора динамического хаоса с фазовым управлением.

Также на программном языке Verilog HDL осуществили обратную связь (рис 15).

Рисунок 15. Программа обратного связи.

Экспериментальные результаты на основе ПЛИС генератора динамического хаоса с фазовым управлением приведена ниже:

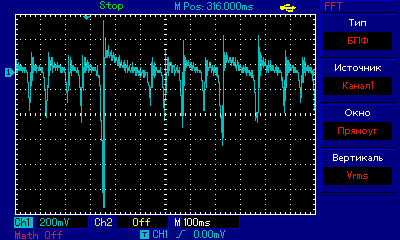
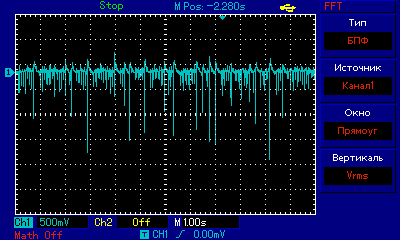
Рисунок 16. Экспериментальные результаты генератора динамического хаоса с фазовым управлением.

Ресурс который ПЛИС использовал для генерации динамического хаоса с фазовым управлением приведена рисунке 17.

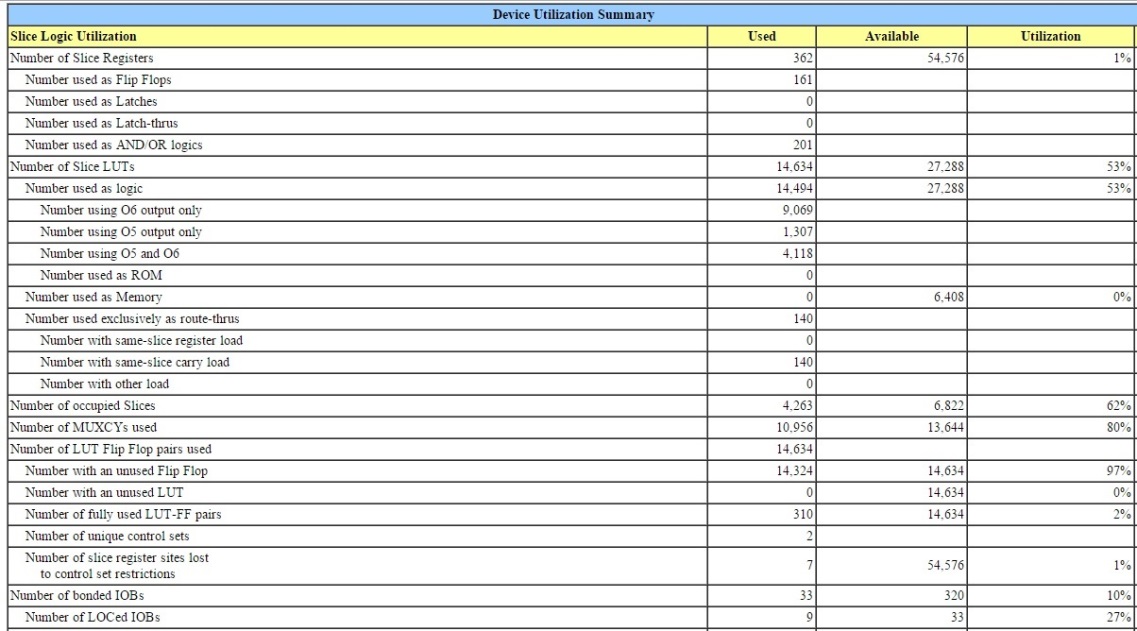
Рисунок 17. Ресурс ПЛИС.

Численные моделирования вышеприведенных систем генераторов хаоса получены экспериментальными методами на основе интегральных схем FPGA в реальном времени. Этот метод является простым способом реализации сложных схемотехнических задач. Точность и частоту реализации сигналов можно повысить за счет параллельных вычислительных методов, также от внешнего ЦАП. Эти результаты могут быть полезными в исследованиях информационных беспроводных системах передачи и приема данных и для повышения их эффективности.

Литература

[1] Z.Zh. Zhanabaev Fractal measures in nanoelectronics and neurodynamics // Eurasian Physical Technical Journal. Vol. 9, №1(17), pp.3-13, 2012.

[2] M.A. Aseeri and M.I. Sobhy Design Chaotic Generator at High Frequencies, Greener Journal of Science, Engineering and Technology Research ISSN: 2276-7835 Vol. 3 (7), pp. 205-209, August 2012.

[3] C. Eroglu, F.A. Savaci Control system for synchronization of generalized Chua’s circuits in FPGA, PHYSCON 2009, Catania, Italy, September, 1–September, 4 2009

[4] M.I. Sobhy, M. A. Aseeri and A. Shehata,” Real time implementation of chaotic models using digital hardware”, AMREM 2002, HPEM 13, June 2002.

[5] L. Pivka, C. W. Wu and A. Huang, “Lorenz equation and Chua’s equation,” Int. J. of Bifurcation and Chaos, vol. 6, No. 12B, pp.2443- 2489, 1996.

Дата добавления: 2014-11-16