Тема 10. Ряды

Основные теоретические сведения.

1. Числовой ряд

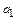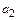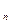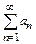+ +…+ а +… = , (1)

называется сходящимися, если существует предел его частичных сумм 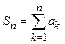. Число 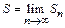называется суммой ряда. Если же предел частичных сумм не существует, то ряд (1) называется расходящимися.

Необходимый признак сходимости: если ряд (1) сходится, то его общий член стремится к нулю при : .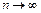

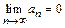К достаточным признакам сходимости рядов с положительными членами (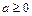) относятся:

а) Признак сравнения в предельной форме: если

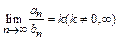, (2)

то ряды 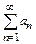и 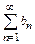одновременно сходится или расходится. В качестве эталонных рядов для сравнения обычно служат:

ряд 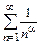сходящийся при 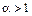и расходящийся при ;

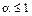ряд 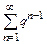, сходящийся при 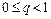и расходящийся .

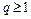б) Признак Даламбера: если существует

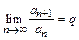, (3)

то ряд 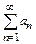сходится при 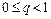и расходится при 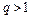. Если же 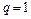, то вопрос о сходимости ряда этим признаком не решается.

Ряд 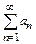с членами, имеющими разные знаки, называется условно сходящимся, если ряд 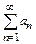сходится, а ряд 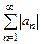расходится, и абсолютно сходящимся, если ряд 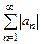сходится.

в) Признак Лейбница: если члены ряда 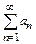удовлетворяют условиям:

1) 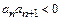(т.е. ряд знакочередующийся); 2) ;

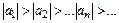3) 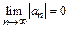, то ряд сходится. Погрешность 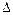, происходящая от замены суммы сходящегося знакочередующегося ряда суммой его первых n членов, по абсолютной величине меньше первого из отброшенных членов:

. (4)

2. Ряд вида

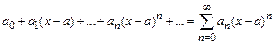(5)

называется степенным рядом [относительно 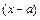], точка 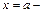центром разложения, 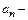коэффициентами ряда. Число 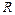называется радиусом сходимости степенного ряда, если ряд (5) сходится при 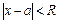и расходится при . При 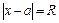ряд может как сходится, так и расходится. Интервал 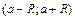называется интервалом сходимости степенного ряда (5). Радиус сходимости R может быть найден по формуле

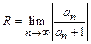. (6)

Степенной ряд (5) внутри интервала сходимости можно почленно дифференцировать и интегрировать с сохранением радиуса сходимости.

Пример 1. Исследовать на сходимость числовой ряд .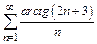

Решение. Проверяем сходимость ряда по признаку Даламбера (3). Так как общий член ряда 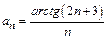, то, заменяя в выражении n- го члена n на n +1, находим . Затем ищем предел отношения последующего члена 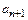к предыдущему 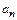при :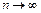

.

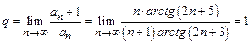Поскольку полученный предел равен единице, признак Даламбера не дает ответа на вопрос о сходимости ряда (здесь для вычисления предела было использовано правило Лопиталя). Применим теперь признак сравнения в предельной форме. В качестве эталонного ряда выберем ряд 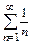, 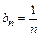и в силу формулы (2) получим

.

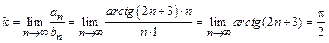Следовательно, исследуемый ряд является расходящимся, так как эталонный ряд с общим членом 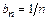расходится (гармонический ряд).

Пример 2. Найти радиус и интервал сходимости степенного ряда 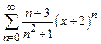. Исследовать сходимость ряда на концах интервала сходимости.

Решение. Радиус сходимости находим по формуле (6):

,

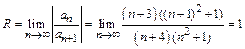Интервал сходимости данного ряда определяется интервалом 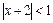или .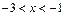

Исследуем концы интервала сходимости. При 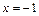получаем числовой ряд

,

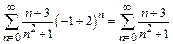расходимость которого может быть установлена с помощью предельного признака сравнения (эталонный ряд – гармонический).

При 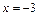получаем числовой ряд

,

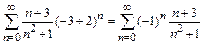который сходится по признаку Лейбница. Так как ряд, составленный из абсолютных членов данного ряда, т.е. ряд 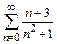, расходится, то исследуемый ряд сходится условно.

Таким образом, интервал сходимости исследуемого степенного ряда имеет вид .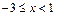

Дата добавления: 2014-11-16