Методические указания. Геометрические характеристики плоских фигур

Геометрические характеристики плоских фигур

Для расчета элементов сооружений и деталей машин на прочность, жесткость и устойчивость необходимо овладеть методами определения геометрических характеристик поперечных сечений.

В тех случаях, когда напряжения распределяются равномерно по всему поперечному сечению, геометрической характеристикой для расчета стержня на прочность и жесткость является только площадь поперечного сечения F:

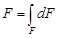, (1)

где dF - элементарные площадки, на которые разбивается вся площадь плоской фигуры.

При неравномерном распределении напряжений по поперечному сечению, имеющем место при кручении, изгибе, внецентренном растяжении и других видах деформаций, прочность и жесткость стержня зависят не только от размеров и материала стержня, но и от формы и расположения поперечных сечений по отношению к действующим нагрузкам.

СТАТИЧЕСКИЕ МОМЕНТЫ ПЛОЩАДИ.

ЦЕНТР ТЯЖЕСТИ ПОПЕРЕЧНОГО СЕЧЕНИЯ

Рассмотрим произвольное поперечное сечение стержня, отнесенное к координатным осям х и у (рис.1), площадь которого равна F.

Рис. 1

Выделим на площади F бесконечно малую площадь dF с координатами х и у. По аналогии с выражением для момента силы относительно данной оси можно составить выражение и для момента площади относительно оси, которое называется статическим моментом. Так, произведения

,

называются статическими моментами элемента площади dF относительно осей х, у.

Статические моменты площади поперечного сечения относительно осей х и у определяются следующим равенством:

, . (2)

Статические моменты имеют размерность см³ и м³.

Пусть х_с, у_с – координаты центра тяжести фигуры (рис.1, точка С).

Координаты центра тяжести фигуры можно выразить через статические моменты:

, . (3)

Статический момент площади сложной фигуры относительно данной оси определяется как сумма статических моментов составных ее частей:

, (4)

где F_i – площадь части фигуры;

x_i, y_i – координаты ее центра тяжести;

n - число составляющих фигур.

Координаты центра тяжести сложной фигуры определяются так:

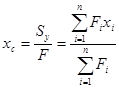, . (5)

Оси, проходящие через центр тяжести сечения, называются центральными. Статический момент площади относительно центральной оси равен нулю.

Моменты инерции плоских фигур

Осевые моменты инерции площади фигуры (рис.1) определяют следующим равенством

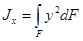, . (6)

Полярным моментом инерции площади фигуры относительно данной точки (полюса 0, рис.1) называется сумма произведений элементарных площадок на квадраты их расстояний от полюса:

. (7)

Если полюс совпадает с началом прямоугольных координат осей х, у, то 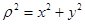и

. (8)

Центробежным моментом инерции называется интеграл произведения площадей элементарных площадок на их расстояния от координатных осей х, у:

. (9)

Моменты инерции (осевые, центробежные, полярные) имеют размерность см⁴ и м⁴.

Осевые и полярные моменты инерции всегда положительны, центробежный момент инерции может быть положительным, отрицательным и равным нулю. Оси, относительно которых центробежный момент равен нулю, называются главными осями инерции.

Основные свойства моментов инерции

1. Момент инерции сложного сечения равен сумме моментов составляющих его фигур:

, ,

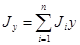(10)

, ,

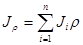где n – число составляющих фигур.

2. Осевой момент инерции площади относительно произвольной оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.

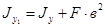, . (11)

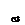
Рис. 2

3. Центробежный момент инерции площади сечения относительно произвольной пары взаимно перпендикулярных осей х₁, у₁ (рис.2) равен центробежному моменту инерции относительно центра осей х, у, им параллельных, плюс произведение площади фигуры на координаты ее центра тяжести в новых осях (с учетом знака)

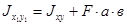. (12)

Из формул (10), (11) следует, что из всех моментов инерции относительно параллельных осей центральные моменты инерции наименьшие.

Рис.3

4. Если известны моменты инерции произвольной фигуры J_x, J_y, J_xy относительно координатных осей х и у, то моменты инерции относительно осей х₁, у₁ (рис.3), повернутых на угол α по отношению к осям х, у, определяются по формулам:

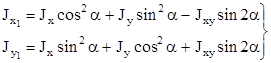(13)

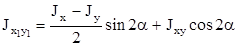(14)

Угол α считается положительным, если он отсчитывается против хода часовой стрелки.

При повороте прямоугольных осей сумма моментов инерции относительно координатных осей остается постоянной и равной полярному моменту инерции относительно начала координат.

Центробежный момент инерции сечения относительно двух взаимно перпендикулярных осей, одна из которых или обе являются осями симметрии, равен нулю.

Главные оси и главные моменты инерции

Две взаимно перпендикулярные оси, относительно которых центробежный момент инерции площади сечения равен нуле, называются главными осями инерции. Моменты инерции относительно главных осей называют главными моментами инерции.

В каждой точке плоскости любого сечения существуют главные оси. Главные оси, проходящие через центр тяжести сечения, называют главными центральными осями.

Для оценки прочности и определения деформаций стержней при различных видах нагружения в соответствующих формулах используются геометрические характеристики сечений относительно главных центральных осей.

Рис.4

Положение главных осей U, V определяется углом α₀, который находится по формуле (рис.4):

(15)

Положительное значение угла α₀ откладывается против хода часовой стрелки.

Главные моменты инерции обладают свойством экстремальности и могут быть вычислены по формуле

(16)

Если сечение имеет ось симметрии, то эта ось и любая ось, ей перпендикулярная, являются главными осями.

Центробежный момент инерции может быть определен так

(17)

v

На рис. 5 показано применение правила для определения знака центробежного момента инерции неравнобокого уголка в зависимости от расположения его относительно осей координат.

u

		v
	у
			у

α<0

х

u

Рис. 5.

Моменты сопротивления плоских сечений

Основным моментом сопротивления сечения относительно главной центральной оси сечения называется отношение момента инерции относительно этой оси к расстоянию от этой оси до наиболее удаленной точки сечения.

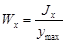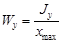; . (18)

Полярным моментом сопротивления называется отношение полярного момента инерции данного сечения относительно выбранного полюса к расстоянию от полюса до наиболее удаленной точки сечения.

. (19)

радиусы инерции. эллипс инерции

Радиусы инерции плоской фигуры относительно осей х и у определяются так:

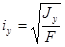; (20)

Главным центральным осям инерции соответствуют главные радиусы инерции

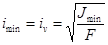; . (21)

Чтобы судить о жесткости поперечного сечения при изучении его геометрических свойств, строят эллипс инерции. Для его построения определяют главные радиусы инерции i_u, i_v, которые являются полуосями эллипса, и откладывают их по осям u, v.

Такой эллипс, называемый эллипсом инерции, обладает тем свойством, что радиус инерции относительно любой центральной оси х определяется как перпендикуляр 0А, опущенный из центра эллипса 0 на касательную к нему, параллельную к оси х. Для получения точки касания надо провести параллельно данной оси х любую хорду. Точка пересечения с линией, соединяющей центр 0 и середину хорды, является точкой касания К. Измерив отрезок 0А=i_x, найдем момент инерции

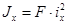. (22)

V

Рис. 6

Дата добавления: 2014-11-16