
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачи 1-20
|
|
|
|
СТРУКТУРНАЯ КЛАССИФИКАЦИЯ МЕХАНИЗМОВ
1.1. Общие понятия и определения
Наукой, которая изучает виды кинематических схем, кинематику и динамику машинных агрегатов в связи с их анализом и синтезом, является теория механизмов и машин (ТММ).
Исследование или проектирование любой конструкции, которая движется, начинается из составления ее кинематической схемы. Такая подвижная конструкция в механике носит название механизма.
Главным объектом исследования в ТММ есть кинематическая схема – условное изображение механизма, на котором в упрощенном виде указаны элементы, которые влияют на его кинематические характеристики. Структурная схема подвижной конструкции, в отличие от кинематической схемы, выполняется произвольно без соблюдения масштаба. Такое изображение дает представление только о структуре конструкции.
Устройства, которые ведут к увеличению производительности работы, частично и целиком заменяют человека в ее трудовых и физиологических функциях, называются машинами (например, ДВЗ – двигатель внутреннего сгорания, ГТД – газотурбинный двигатель, паровые турбины, электродвигатели, генератор тока, компрессор, насос, и т.д.).
Механизм – это система искусственно созданных тел (твердых, жидких и газообразных), предназначенная для преобразования заданного движения одних тел в требуемые движения других тел (лебедка, грузоподъемный кран, механизмы гидравлических поводов, обрабатывающих станков, шпили, брашпили и т.д.). Главное внимание в ТММ уделяют механизмам, которые состоят из твердых тел.
Таким образом, роль механизма, в отличие от машины, сводится лишь к передаче движения и потока энергии. В то же время механизм имеет ту же структуру, которая и машина, и в этом отношении между ними нет никакого расхождения. Механизм можно считать машиной, если он в условиях движения преодолевает внешние сопротивления, связанные непосредственно с процессом производства или транспорта. При работе вхолостую машину можно рассматривать как механизм в чистом виде.
Машина и механизмы объединяются в машинные агрегаты. Машинный агрегат – это комплекс взаимосвязанных машин, механизмов, устройств, исполнительных органов и т.п., предназначенный для выполнения определенных функций.
Структурной единицей любой подвижной конструкции является звено. Звеном называют одну или группу деталей, жестко соединенных между собой. Звенья бывают подвижными (поршень, шестерня, вал и т.п.) и неподвижными (станина, фундамент, цилиндровая втулка и т.п.). Неподвижные звенья состоят из ряда жестко связанных тел и называются стойками. Любой механизм имеет только одно неподвижное и несколько подвижных звеньев.
Входным считают звено, закон движения которого задан и превращается механизмом в нужный закон движения других звеньев. Оно может совпадать или не совпадать с ведущим звеном, которое с помощью внешних нагрузок обеспечивает движение всего механизма. Ведомым называют звено, которое осуществляет движение, для выполнения которого предназначен механизм. Остальные звенья механизма называют промежуточными.
Звенья бывают простые и сложные. Если звено входит не более, чем в два подвижных соединения с другими звеньями (рис. 1.1, а, б), то оно является простым, в других случаях (рис. 1.1, в) звено будет сложным.
 а
а
|  б
б
|  в
в
|
Рис. 1.1. Простые (а, б) и сложные (в) звенья механизмов
На схемах звенья обозначают арабскими цифрами, кинематические пары – большими латинскими буквами. Неподвижное звено, которое входит в состав механизма, называют стойкой или станиной. На кинематических схемах неподвижные звенья обозначают штриховкой. Подвижное звено, которое осуществляет полный оборот, называют кривошипом. Звенья, которые осуществляют колеблющееся, плоскопаралельное и возвратно-поступательное движения, соответственно называют коромыслом, шатуном и ползуном. Подвижное звено, которое является направляющим для ползуна, называют кулисой. Ползун, движущийся по кулисе, называют камнем кулисы.
1.2. Классификация кинематических пар
Каждый механизм состоит из звеньев. Подвижное соединение двух звеньев называется кинематической парой (рис.1.2).
Между двумя звеньями может существовать только одно подвижное соединение или кинематическая пара, несмотря на то, что эти звенья могут иметь контакт в нескольких местах. Нужно также отметить, что в случае столкновенья в одном месте нескольких звеньев, они создают между собой общее количество пар, которые на единицу меньше количества звеньев, которые совпадают в этом месте.
Поверхности, линии, или точки, которыми одно звено затрагивает другой, называют элементами кинематических пар.
Кинематические пары классифицируют по четырем признакам.
1. По числу связей, т.е. ограничений, которые кинематическая пара накладывает на относительное движение звеньев. За этим признаком пары делятся на пять классов. Класс кинематической пары определяют за числом связей  , где
, где 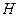 – количество степеней вольности в относительном движении звеньев, которые образовывают пару.
– количество степеней вольности в относительном движении звеньев, которые образовывают пару.
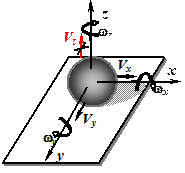
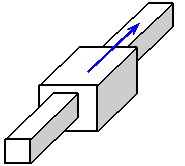
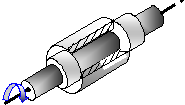
2. По виду элементов контакта звеньев в паре они разделяются на высшие и низшие. К высшим принадлежат пары, в которых звенья соединяются по поверхности (рис.1.2, б, в, ж), низшими – звенья, в которых элементами контакта являются точки или линии (рис.1.2, г, д, е, с, и).
3. По характеру относительного движения звеньев пары могут быть плоскими (рис.1.2, г, ж, з, и) и пространственными (рис.1.2, б, в, д, е).
4. По условиям поддержки контакта звеньев в пари они разделяются на открытые (рис.1.2, б, в, г) и закрытые (рис.1.2, д, е, ж, з, и). В открытых звеньях нужное силовое замыкание контакта, в закрытых этот контакт обеспечивается геометрическим замыканием, т.е. с помощью особенностей формы контактирующих поверхностей.
   a б в
a б в
|
   г д е
г д е
|
   ж з и
ж з и
|
Рис. 1.2. Примеры разнообразных видов кинематических пар:
а – независимое или свободное твердое тело (снопа) с шестью степенями вольности; бы – кинематическая пара І класса «снопа – плоскость»; в – кинематическая пара ІІ класса «цилиндр – плоскость»; г – кинематическая пара ІІІ класса «плоское тело – плоскость»; д – кинематическая пара ІІІ класса, сферический шарнир; е – кинематическая пара ІV класса, контакт звеньев по цилиндрической поверхности; ж – кинематическая пара ІV класса в контакте зубчатых колес; з – поступательнаякинематическая пара V класса; и – вращательная кинематическая пара V класса
Системы звеньев, которые соединены между собой кинематическими парами, называют кинематическими цепями.
1.3. Степень подвижности механизма
Механизмом называют кинематическую цепь с неподвижным звеном, в котором при заданном движении одного или нескольких звеньев относительно любого из них все другие звенья делают однозначно обусловленные движения.
Количество обобщенных координат, которые целиком характеризуют положение и движение тела или механизма, принято называть числом степеней свободы (степенью подвижности) тела или механизма.
Характер движения механизма определяется размерами звеньев, последовательностью их соединения, конструкцией кинематических пар. Количество степеней свободы или степень подвижности механизма определяется по структурной формуле Сомова – Малышева
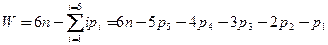 , (1.1)
, (1.1)
где  – количество подвижных звеньев механизма;
– количество подвижных звеньев механизма; 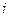 – номер класса кинематической пары;
– номер класса кинематической пары; 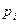 – количество кинематических пар, принадлежат к классу за номером
– количество кинематических пар, принадлежат к классу за номером 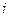 .
.
Большая часть кинематических схем механизмов имеет некоторое количество  общих, или совпадающих условий связи, поэтому подсчитывание степени подвижности должно выполняться по условию их отнимания из всех коэффициентов того числа
общих, или совпадающих условий связи, поэтому подсчитывание степени подвижности должно выполняться по условию их отнимания из всех коэффициентов того числа  . Общую структурную формулу с учетом общих связей вывел в 1943 году В.В. Добровольский
. Общую структурную формулу с учетом общих связей вывел в 1943 году В.В. Добровольский
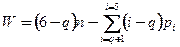 . (1.2)
. (1.2)
Для плоских механизмов количество совпадающих условий связи равняется трем (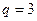 ), поэтому степень подвижности определяется по формуле, полученной П.Л. Чебышевым в 1869году
), поэтому степень подвижности определяется по формуле, полученной П.Л. Чебышевым в 1869году
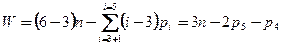 . (1.3)
. (1.3)
где  – количество подвижных звеньев;
– количество подвижных звеньев; 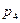 и
и  – количество кинематических пар, соответственно IV и V классов.
– количество кинематических пар, соответственно IV и V классов.
В представленной кинематической схеме (табл. 1.1) указано только направление движения входного звена. Необходимо определить звенья, кинематические пары и указать их на кинематической схеме. Подсчитать по структурной формуле Чебышева (1.3) степень подвижности 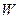 . Последовательность решения этой задачи рассмотрим на конкретном примере.
. Последовательность решения этой задачи рассмотрим на конкретном примере.
Таблица 1.1. Кинематические схемы к задачам 1 – 20
 1. Механизм автомата перекоса вертолета
1. Механизм автомата перекоса вертолета
|  2.Механизм миксера
2.Механизм миксера
|
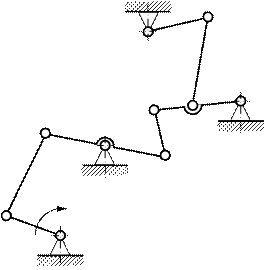
 3.Механизм тестомешалки
3.Механизм тестомешалки
|  4.Механизм управления тормозными колодками
4.Механизм управления тормозными колодками
|
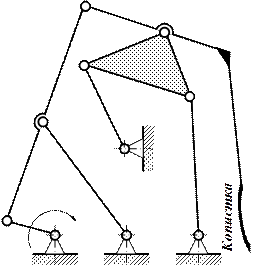
 5.Механизм отрезных ножниц
5.Механизм отрезных ножниц
|  6.Механизм шасси самолета
6.Механизм шасси самолета
|
 7. Муфта Ольдгейма
7. Муфта Ольдгейма
| 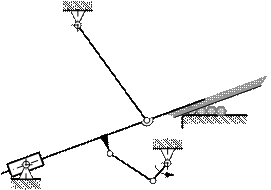 8. Механизм разрезания прутков
8. Механизм разрезания прутков
|
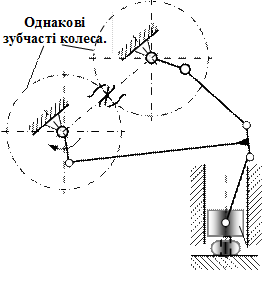 9. Механический пресс для штампования деталей
9. Механический пресс для штампования деталей
| 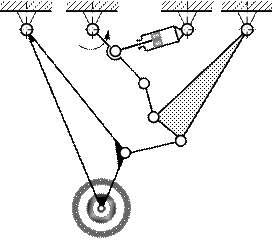 10.Механизм шасси самолета
10.Механизм шасси самолета
|
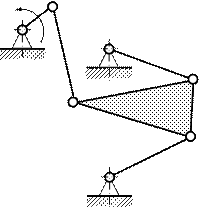 11. Механизм Робертса
11. Механизм Робертса
|  12. Механизм приемника давления электрического дистанционного манометра
12. Механизм приемника давления электрического дистанционного манометра
|
 13 Механизм пресса
13 Механизм пресса
| 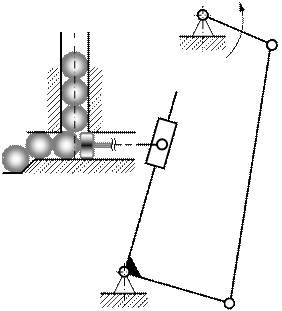 14.Механизм подачи деталей к транспортеру
14.Механизм подачи деталей к транспортеру
|
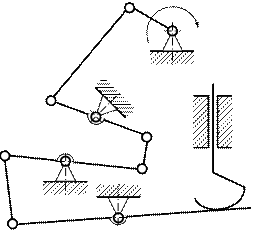 15. Механизм управления клапаном
15. Механизм управления клапаном
|  16. Поплавковый топливомер
16. Поплавковый топливомер
|
 17. Долбежный станок
17. Долбежный станок
| 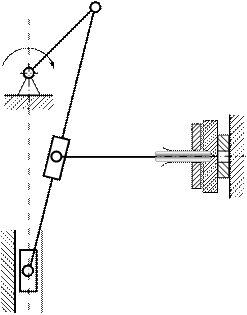 18. Перфорационный станок для прошивки отверстий в листовом материале
18. Перфорационный станок для прошивки отверстий в листовом материале
|
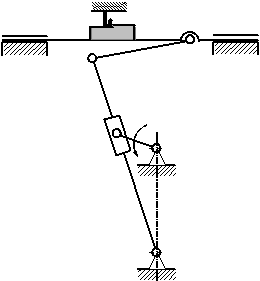 19.Поперечно-строгальный станок
19.Поперечно-строгальный станок
|  20. Водяной насос
20. Водяной насос
|
Пример 1.
Определить звенья и кинематические пары механизма Дизеля (рис. А). Подсчитать по структурной формуле Чебышева степень подвижности.
Рис. А. Схема механизма Дизеля без обозначений звеньев и кинематических пар
Решение задачи начнем с определения звеньев и кинематических пар (рис. а). В состав представленной схемы входят: стойка 0, кривошип 1, шатуны 2, 4, 6, коромысло 5, ползуны 3 и 7. Все звенья указаны на схеме арабскими цифрами (рис. б). Кроме стойки 0, все другие звенья являются подвижными. Таким образом, количество подвижных звеньев в представленной схеме равняется 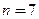 . Звенья механизма соединены между собой следующими кинематическими парами: вращательные пары или шарниры O, A, B, D, K, F, G, H; поступательные пары C и L (рис. б).
. Звенья механизма соединены между собой следующими кинематическими парами: вращательные пары или шарниры O, A, B, D, K, F, G, H; поступательные пары C и L (рис. б).
Все перечисленные пары принадлежат к пятому классу по количеству ограничений, их общее количество 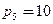 . Кинематические пары четвертого класса в представленной схеме отсутствуют,
. Кинематические пары четвертого класса в представленной схеме отсутствуют, 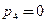 . Подсчитаем степень подвижности по структурной формуле
. Подсчитаем степень подвижности по структурной формуле 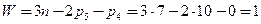 . Весь механизм имеет одну степень свободы.
. Весь механизм имеет одну степень свободы.

Рис Б. Схема механизма Дизеля с обозначениями звеньев и кинематических пар
Полный ответ: 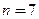 ;
; 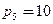 ;
; 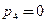 ;
; 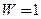 .
.
Пример 2.
Определить звенья и кинематические пары механизма мальтийского креста (рис. В). Подсчитать по структурной формуле Чебышева степень подвижности.
Решение задачи, как в предыдущем примере, начнем с определения звеньев и кинематических пар (рис. В).
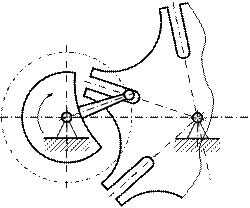
Рис. В. Механизм мальтийского креста высоковольтного выключателя
В состав представленной схемы входят: стойка 0, кривошип 1 с цевкой и мальтийский крест 2 с шестью пазами. Все звенья указаны на схеме арабскими цифрами (рис. б). Кроме стойки 0, все другие звенья являются подвижными. Таким образом, количество подвижных звеньев в представленной схеме равняется 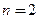 . Подвижные звенья механизма соединены со стойкой двумя вращательными парами O и О2 (рис. с), которые являются парами пятого класса. Цевка ручки 1 движется в пазах креста 2 и образует с ним высшую кинематическую пару А четвертого класса. Таким образом,
. Подвижные звенья механизма соединены со стойкой двумя вращательными парами O и О2 (рис. с), которые являются парами пятого класса. Цевка ручки 1 движется в пазах креста 2 и образует с ним высшую кинематическую пару А четвертого класса. Таким образом,  и
и 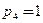 .
.
По формуле Чебышева определяем степень подвижности 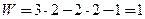 . Как в предыдущем примере, механизм имеет одну степень свободы, но в отличие от него, ведомое звено 2 движется прерывисто.
. Как в предыдущем примере, механизм имеет одну степень свободы, но в отличие от него, ведомое звено 2 движется прерывисто.
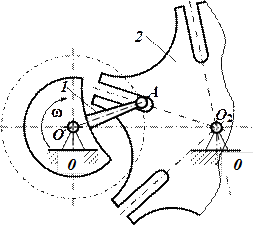
Рис. Г. Механизм мальтийского креста с обозначениями звеньев и кинематических пар
Полный ответ: 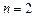 ;
;  ;
; 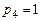 ;
;  .
.
1.4. Избыточные (пассивные) связи и лишние степени свободы
Кроме связей, которые активно влияют на характер движения механизмов, в них могут встретиться условия связи и степени свободы, которые не влияют на движение звеньев механизма в целом. Изъятие из механизмов звеньев и кинематических пар, которым эти степени свободы и условия связи принадлежат, может быть сделано без изменения общего характера движения механизма в целом. Такие связи называются избыточными или пассивными связями, а степени свободы лишними степенями свободы.
Иногда лишнюю связь сознательно внедряют в состав механизма для повышения его жесткости или для устранения неопределенности движения звеньев в некоторых положениях. Включение в состав механизма таких звеньев должно происходить с выполнением дополнительных условий. Например, звено 4 входит в состав шарнирного механизма при выполнении дополнительных условий  и
и 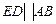 (рис.1.3, б). Действительно, степень подвижности механизма со звеном 4 согласно расчету
(рис.1.3, б). Действительно, степень подвижности механизма со звеном 4 согласно расчету 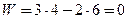 равняется нулю. Этот результат соответствует действительности только относительно статически определимой фермы (рис.1.3, а), которая построена без соблюдения упомянутых условий. Но при выполнении дополнительных условий
равняется нулю. Этот результат соответствует действительности только относительно статически определимой фермы (рис.1.3, а), которая построена без соблюдения упомянутых условий. Но при выполнении дополнительных условий  и
и 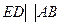 звено 4 только дублирует связи звена 2 и не создает препятствий движению других звеньев, т.е. накладывает на движение механизма условия связи, которая являются избыточными. Поэтому при теоретическом исследовании она должна быть отброшена. Только изъяв из механизма избыточное звено с двумя кинематическими парами, получим шарнирный параллелограмм (рис. 1.3, в) с одной степенью свободы,
звено 4 только дублирует связи звена 2 и не создает препятствий движению других звеньев, т.е. накладывает на движение механизма условия связи, которая являются избыточными. Поэтому при теоретическом исследовании она должна быть отброшена. Только изъяв из механизма избыточное звено с двумя кинематическими парами, получим шарнирный параллелограмм (рис. 1.3, в) с одной степенью свободы,  .
.
 а а
|  бы бы
|  в
в
|
Рис. 1.3. Многозвенные шарнирные конструкции
а – статически определенная ферма; бы – шарнирный параллелограмм с пассивными связями; в – шарнирный параллелограмм
Для плоского кулачкового механизма, (рис. 1.4, а), если считать, что ролик 3 жестко связаны с толкателем 2, то степень подвижности 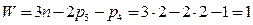 .
.
Но, если считать ролик свободно вращающимся, то формальный расчет приведет к следующему результату  , т.е. ролик вносит лишнюю степень свободы и фактически при подсчете степени подвижности механизма это вращательное движение приниматься во внимание не должно. Эта степень может быть реализованной только в случаях, когда его форма не будет идеальной круглой, или ось вращательной пары не будет совпадать с центром круга (рис. 1.4, б).
, т.е. ролик вносит лишнюю степень свободы и фактически при подсчете степени подвижности механизма это вращательное движение приниматься во внимание не должно. Эта степень может быть реализованной только в случаях, когда его форма не будет идеальной круглой, или ось вращательной пары не будет совпадать с центром круга (рис. 1.4, б).
При исследовании механизмов с лишними степенями свободы рабочий профиль заменяется на теоретический (рис. 1.4, в), который совпадает с траекторией обратного движения ролика 3 вокруг неподвижного рабочего профиля (указано штрихпунктиром на рис. 1.4, а).
 а
а
|  б
б
|  в в
|
Рис. 1.4. Кулачковый механизм с лишней степенью подвижности (а), с двумя степенями (б) и с теоретическим профилем
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 2642; Нарушение авторских прав?; Мы поможем в написании вашей работы!