
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Черт. 49. К примерам расчета 33, 34 и 39
|
|
|
|
Расчет в плоскости изгиба. Принимаем расчетную толщину полки равной средней высоте свесов h¢f = hf = 200 + 30/2 = 215 мм.
Вычислим площадь и момент инерции бетонного сечения:
 мм2;
мм2;

Радиус инерции сечения  мм.
мм.
Так как l 0/ i = 16 200/520 = 31,1 < 35 и l 0/ i > 14, расчет производим с учетом прогиба элемента согласно п. 3.54, принимая значение Ncr равным:
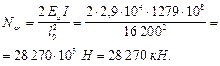
Коэффициент h определим по формуле (91):
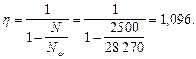
Центр тяжести площади арматуры As и A¢s отстоит от ближайшей грани на расстоянии а = а¢ =  мм, откуда h 0 = h – a = 1500 – 79 = 1421 мм.
мм, откуда h 0 = h – a = 1500 – 79 = 1421 мм.
Значение е с учетом прогиба элемента равно:
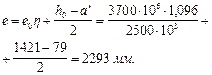
Проверим условие (130):

т. е. расчет производим как для двутаврового сечения.
Площадь сжатых свесов полки равна:
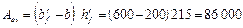 мм2.
мм2.
Определим высоту сжатой зоны:
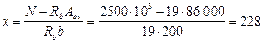 мм.
мм.
Из табл. 18 находим xR = 0,523. Так как х = 228 мм < xR h 0 = 0,523 · 1421 = 743 мм, прочность сечения проверим из условия (131):
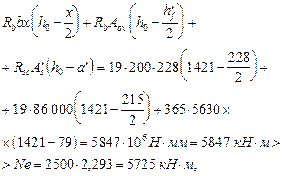
т. е. прочность сечения в плоскости изгиба обеспечена.
Расчет из плоскости изгиба. Определим радиус инерции сечения из плоскости изгиба:
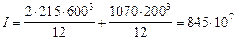 мм4;
мм4;
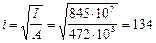 мм.
мм.
Так как гибкость из плоскости изгиба l 0/ i = 10 800/134 = 80 значительно превышает гибкость в плоскости изгиба l 0/ i = 31,1, согласно п. 3.51 проверим прочность сечения из плоскости изгиба, принимая эксцентриситет е 0 равным случайному эксцентриситету еа. Высота сечения при этом равна h = 600 мм.
Поскольку случайный эксцентриситет, согласно п. 3.50, еа = 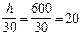 мм
мм  мм, принимаем еа =
мм, принимаем еа = 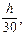 что при
что при 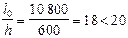 позволяет производить расчет, согласно п. 3.64, как для прямоугольного сечения, не учитывая в „запас” сечение ребра, т. е. принимая b = 2 · 215 = 430 мм.
позволяет производить расчет, согласно п. 3.64, как для прямоугольного сечения, не учитывая в „запас” сечение ребра, т. е. принимая b = 2 · 215 = 430 мм.
Площадь сечения промежуточных стержней, расположенных вдоль обеих полок, равна As,int = 4826 мм2 (6 Æ 32), а площадь сечения всех стержней As,tot = 11 260 мм2 (14 Æ 32). Поскольку As,tot /3 = 11 260/3 = 3750 мм2 < As,int = 4826 мм2, в расчете используем табл. 27 (разд. Б). Из табл. 27 для тяжелого бетона при Nl/N = 2000/2500 = 0,8 и l 0/ h = 10,8/0,6 = 18 находим jsb = 0,724.
Значение 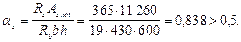 Следовательно, j = jsb = 0,724.
Следовательно, j = jsb = 0,724.
Проверим условие (119):
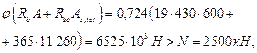
т. е. прочность сечения из плоскости изгиба обеспечена.
Пример 34. Дано: размеры сечения и расположения арматуры ¾ по черт. 49; бетон тяжелый класса В30 (Rb = 19 МПа при gb 2 = 1,1; Eb = 2,9 · 104 МПа); арматура симметричная класса A-III (Rs = Rsc = 365 МПа); продольная сила N = 6000 кН; изгибающий момент М = 3100 кН·м; расчетная длина элемента: в плоскости изгиба l 0 = 16,2 м, из плоскости изгиба l 0 = 10,8 м.
Требуется определить площадь сечения арматуры.
Расчет в плоскости изгиба. Из примера 33 имеем: h¢f = 15 мм; h 0 =1421 мм; а¢ = 79 мм; Ncr = 28 270 кН.
По формуле (91) определим коэффициент h:

Значение е с учетом прогиба элемента равно:
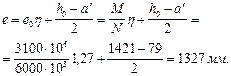
Проверим условие (130):
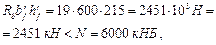
т. е. расчет производим как для двутаврового сечения.
Площадь сжатых свесов полки равна:
 мм2.
мм2.
Определим значения an, am 1, aov, am,ov, d:
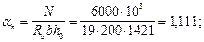
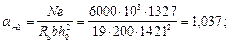
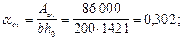

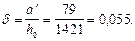
Из табл. 18 находим xR = 0,523.
Так как x = an – aov = 1,111 – 0,302 = 0,809 > xR = 0,523, площадь арматуры определим по формуле (135). Для этого по формулам (136) и (132) вычислим значения as и 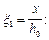

Из табл. 18 находим yс = 3,0 и w = 0,698.

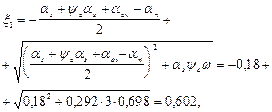
отсюда

Принимаем As = A¢s = 5630 мм2 (7 Æ 32).
Расчет из плоскости изгиба производим аналогично примеру 33.
КОЛЬЦЕВЫЕ СЕЧЕНИЯ
Пример 35. Дано: сечение с внутренним радиусом r 1 = 150 мм, наружным ¾ r 2 = 250 мм; бетон тяжелый класса В25 (Rb = 16 МПа при gb 2 = 1,1); продольная арматура класса A-III (Rs = Rsc = 365 МПа); площадь ее сечения As,tot = 1470 мм2 (13 Æ 12); продольная сила от полной нагрузки N = 1200 кН, ее эксцентриситет относительно центра тяжести сечения с учетом прогиба элемента равен е 0 = 120 мм.
Требуется проверить прочность сечения.
Расчет. Вычислим площадь кольцевого сечения:
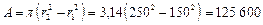 мм2
мм2
Относительная площадь сжатой зоны бетона равна:
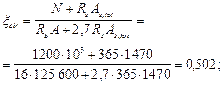
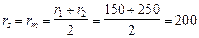 мм.
мм.
Так как 0,15 < xcir = 0,502 < 0,6, прочность сечения проверим из условия (138):
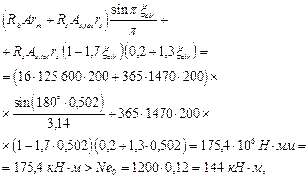
т. е. прочность сечения обеспечена.
КРУГЛЫЕ СЕЧЕНИЯ
Пример 36. Дано: сечение диаметром D = 400 мм; а = 35 мм; бетон тяжелый класса В25 (Rb = 13 МПа при gb 2 = 0,9; Eb = 2,7 · 104 МПа); продольная арматура класса A-III (Rs =Rsc = 365 МПа; Es = 2 · 105 МПа); площадь ее сечения As,tot = 3140 мм2 (10 Æ 20); продольные силы и изгибающие моменты: от постоянных и длительных нагрузок Nl = 400 кН·м; от всех нагрузок N = 600 кН, М = 140 кН·м; расчетная длина элемента l 0 = 4 м.
Требуется проверить прочность сечения.
Расчет. Вычислим:
площадь круглого сечения 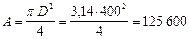 мм2;
мм2;
радиус инерции сечения 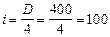 мм;
мм;
гибкость элемента 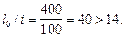
Следовательно, расчет производим с учетом влияния прогиба элемента согласно п. 3.54, а значение Ncr определим по формуле (92). Для этого вычислим:
 мм;
мм;
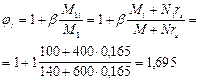
[здесь b = 1,0 (см. табл. 16)];

Так как 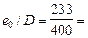 0,583 > de,min = 0,5 – 0,01 l 0/ D – 0,01 Rb, принимаем de = e 0/ D = 0,583.
0,583 > de,min = 0,5 – 0,01 l 0/ D – 0,01 Rb, принимаем de = e 0/ D = 0,583.
Моменты инерции бетонного сечения и всей арматуры соответственно равны:
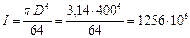 мм4;
мм4;
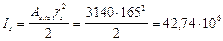 мм4;
мм4;

Тогда
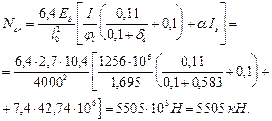
Коэффициент h определим по формуле (91):

Прочность сечения проверим с помощью графика черт. 41.
По значениям 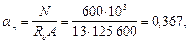
 0,702 и
0,702 и 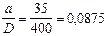 на графике находим am = 0,51.
на графике находим am = 0,51.
Поскольку amRbAr = 0,51 · 13 · 125 600 · 200 = 167 · 106 Н·мм = 167 кН·м > Ne h = 600 · 0,233 · 1,12 = 156,6 кН·м, прочность сечения обеспечена.
Пример 37. По данным примера 36 необходимо подобрать продольную арматуру, пользуясь графиком черт. 41.
Расчет. Из примера 36 i = 100 мм, А = 125 600 мм2, rs = 165 мм. Поскольку l 0/ i = 4000/100 40 > 35, арматуру подбираем с учетом влияния прогиба элемента, вычисляя значение Ncr по формуле (92).
В первом приближении принимаем As,tot = 0,01 A = 1256 мм2, откуда  мм4.
мм4.
Из примера 36 jl = 1,695, de = 0,583, I = 1256 · 106 мм4.
Тогда
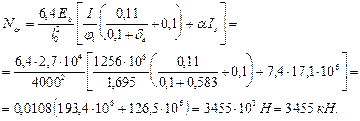
Значение коэффициента 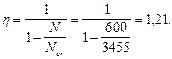
По значениям 
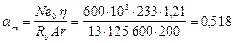 находим as = 0,74, откуда
находим as = 0,74, откуда 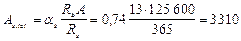 мм2.
мм2.
Поскольку полученное армирование существенно превышает принятое в первом приближении (As,tot = 1256 мм2), значение As,tot = 3310 мм2 определено с „запасом”, и его можно несколько уменьшить, уточнив значение Ncr.
Принимаем  мм2 и производим аналогичный расчет:
мм2 и производим аналогичный расчет:
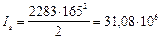 мм4;
мм4;
 кН;
кН;
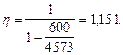
По значениям 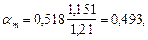 an = 0,367 и
an = 0,367 и  на графике черт. 41 находим as = 0,68.
на графике черт. 41 находим as = 0,68.
 мм2.
мм2.
Принимаем As,tot = 3142 мм2 (10 Æ 20).
ЭЛЕМЕНТЫ, РАБОТАЮЩИЕ
НА КОСОЕ ВНЕЦЕНТРЕННОЕ СЖАТИЕ
Пример 38. Дано: прямоугольное сечение колонны размерами b = 400 мм, h = 600 мм; бетон тяжелый класса В25 (Rb = 16 МПа при gb 2= 1,1); продольная арматура класса A-III (Rs = Rsc = 365 МПа) расположена в сечении согласно черт. 50; в сечении одновременно действуют продольная сила N = 2600 кН и изгибающие моменты: в плоскости, параллельной размеру h, – Mx = 240 кН·м и в плоскости, параллельной размеру b, – My = 182,5 кН·м; моменты Мх и Мy даны с учетом прогиба колонны.
Требуется проверить прочность сечения.

|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 546; Нарушение авторских прав?; Мы поможем в написании вашей работы!