
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Структурные средние. При изучении статистической совокупности применяются такие ее характеристики, которые описывают количественно ее структуру
|
|
|
|
При изучении статистической совокупности применяются такие ее характеристики, которые описывают количественно ее структуру, строение.
Структурные средние характеризуют особенности структуры исследуемой совокупности.
Квантили – значения признака, занимающие в упорядоченном ряду единиц совокупности определенное место. Квантили делят ряд на равные (по числу единиц) части: квартили – на четыре; квинтили – на пять; децили – на десять; перцентили – на сто частей.
Перцентиль – это значение признака в определенной позиции ранжированного ряда, мера относительной позиции варианта в ряду. Р -тый перцентиль – это значение признака, слева от которого лежит Р % вариантов ряда. Позиция Р -го перцентиля задается как (n+1)Р/100, где n -число вариантов ряда.
В статистике наиболее часто применяются квантили, которые делят ряд на четыре равные части – квартили (от латинского слова quarta - четверть).
Первый квартиль (25-й перцентиль) – это значение признака, слева от которого лежит 1/4 (или 25%) всех вариантов.
Второй квартиль – это 50-й перцентиль или медиана. Медиана – значение признака, относительно которого совокупность делится на две равные по числу вариантов части.[11]
Третий квартиль - это точка, слева от которой находится 3/4 или 75% вариантов ряда.
25-й перцентиль называют – нижним квартилем (Q1,), 50-й перцентиль (медиану) – средним квартилем (Q2), 75-й перцентиль – верхним квартилем (Q3).
В статистическом анализе также часто применяют квантили, которые делят совокупность на десять равных частей – децили. Их значения определяются соответственно как 10, 20,..., 90 перцентили.
Отдельно рассмотрим моду и медиану.
Медиана – значение изучаемого признака, приходящееся на середину упорядоченного (ранжированного) ряда.
Мода – значение изучаемого признака, повторяющееся с наибольшей частотой.
В таблице 4.1 представлены формулы для расчета моды и медианы для дискретного и интервального рядов.
Таблица 4.1
Формулы для расчета моды и медианы
| Мода | Медиана |
| Дискретный ряд | |
Определяется как значение признака  , наиболее часто повторяющееся, т.е. с наибольшей частотой. , наиболее часто повторяющееся, т.е. с наибольшей частотой.
| Определяется: 1) при нечетном числе единиц совокупности: определяется как значение признака, расположенное посередине упорядоченного ряда (50-ый перцентиль, второй квартиль); 2) при четном числе единиц совокупности: определяется как среднее двух центральных значений. |
| Интервальный ряд | |
1. Определяем модальный интервал как интервал с наибольшей частотой.
2. Используем формулу:
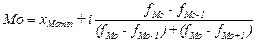 , (4.3)
где , (4.3)
где  - нижняя граница модального интервала; - нижняя граница модального интервала;
 - длина модального интервала; - длина модального интервала;  - частота модального интервала; - частота модального интервала; 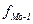 - частота интервала, предшествующего модальному; - частота интервала, предшествующего модальному;  - частота интервала, следующего за модальным. - частота интервала, следующего за модальным.
| 1. Находим ряд накопленных частот  .
2. Определяем медианный интервал как тот, в котором накопленная численность единиц совокупности составляет более половины от их общего числа.
3. Используем формулу: .
2. Определяем медианный интервал как тот, в котором накопленная численность единиц совокупности составляет более половины от их общего числа.
3. Используем формулу:
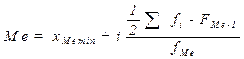 , (4.4)
где , (4.4)
где  - нижняя граница медианного интервала; - нижняя граница медианного интервала;  - длина медианного интервала; - длина медианного интервала;  - частота медианного интервала; - частота медианного интервала; 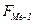 - накопленная частота интервала, предшествующего медианному. - накопленная частота интервала, предшествующего медианному.
|
В общем случае квантили интервального вариационного ряда определяются по формуле:
 , (4.5)
, (4.5)
где х Qp(min) - нижняя граница интервала, в котором находится квантиль;
k - величина квантильного интервала (интервальная разность);
VQp-1 - накопленная частота или частость интервала, предшествующего квантильному;
Р - доля признаков, находящихся левее квантиля (например, для верхнего квартиля -0,25, для медианы -0,5, для седьмого дециля - 0,7);
Σfi - сумма всех частот;
fQp - частота квантильного интервала.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 472; Нарушение авторских прав?; Мы поможем в написании вашей работы!