Примеры применения количественных методов выработки решений

Станковая задача

Современные методы управления тесно связаны с количественными обоснованиями принимаемых решений, с широким использованием экономико-математических методов и моделей управления производством.

Представим себе, например, группу из трех станков, каждый из которых может производить два типа деталей, назовем их условно деталями А и Б. Производительность каждого из станков по разным типам деталей, как правило, различна:

станок № 1 производит в одну минуту 5 деталей А или 5 деталей Б,

станок № 2 производит в одну минуту 6 деталей А или 2 детали Б,

станок № 3 производит в одну минуту 5 деталей А или 3 детали Б.

Задача осложняется тем, что требуется выполнить два важных условия или, как говорят в математике, учесть два ограничения:

– ни один из станков не должен простаивать;

– продукция должна быть комплектна, т. е. количество произведенных деталей А должно равняться количеству деталей Б (это, например, могут быть гайки и болты).

Несмотря на кажущуюся простоту задачи, ни одним из существовавших ранее методов она не решалась. Попробуем и мы, опуская некоторые несущественные подробности, решить столь поучительную задачу. Прежде всего, попытаемся, как, наверное, сделали и те, кто впервые столкнулся с этой задачей, получить ее глазомерное решение.

Все расчеты будем производить исходя из общей продолжительности времени работы в 6 часов = 360 минут (одна смена). Попробуем на все это время загрузить станок № 1 деталями А. Станки № 2 и № 3 также загрузим на все время работы, но деталями Б. Результат такого глазомерного решения изобразим следующим образом: слева от вертикальной черты покажем время загрузки станков по различным деталям, а справа – соответствующее количество произведенной продукции (произведение времени работы на минутную производительность).

Итак, глазомерное решение см. в табл. 7.2.

Таблица 7.2

	Станок	Продолжительность работы станка, мин	Производительность станка (количество деталей за время работы)
	А	Б	А	Б
	№1
	№2
	№3
	Общее количество 1800 + 1800 = выпущенной продукции = 3600 деталей

Глазомерное решение полностью отвечает поставленным условиям: во-первых, все станки полностью загружены в течение рабочего времени; во-вторых, количество произведенных деталей А равно количеству деталей Б. Остается, однако, открытым главный вопрос планирования: является ли наше глазомерное решение наилучшим в данных условиях? Нельзя ли составить другой план распределения станков, который отличался бы от глазомерного наибольшей производительностью?

Обоснованием такого оптимального решения занимается математическое программирование. Суть метода удобнее всего выразить с помощью наглядного геометрического представления, графика (рис. 7.3). Здесь показан построенный по правилам математического программирования многоугольник OABCD (он заштрихован). Многоугольник соответствует условиям нашей задачи и представляет собой область допустимых планов распределения времени работы станков № 2 и № 3 над деталью А. По соответствующим осям графика отмечена продолжительность работы этих станков. (В своих расчетах мы вполне можем обойтись двумя станками и одной деталью, так как по этим данным нетрудно рассчитать и все остальные.)

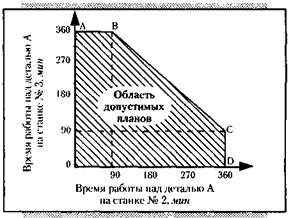
Рис. 7.3. График решения станковой задачи

Любая точка заштрихованной области допустимых планов, как видно из ее названия, даст нам какой-либо один возможный план, отвечающий обоим принятым условиям – ограничениям. Так, например, точка О соответствует нашему глазомерному плану: время работы над деталью А на станках № 2 и № 3 равно нулю.

В поисках наилучшего плана посмотрим, какой план распределения станков дает другие точки области. Вот, скажем, точка В. Как видно из графика, этой точке соответствует время работы над деталью А станка № 2, равное 90 минутам, станка № 3 – 360 минутам. По этим данным нетрудно составить второй план распределения станков, причем время, отводимое на производство детали Б станками № 2 и № 3, получится как дополнение до 360 минут времени, снятого с графика,– станки не должны простаивать. Что касается станка № 1, то его время работы подбирается таким, чтобы общее количество деталей А и Б совпадало.

Второе решение, следовательно, будет выглядеть так (табл. 7.3).

Таблица 7.3

	Станок	Продолжительность работы станка, мин	Производительность станка (количество деталей за время работы)
	А	Б	А	Б
	№1
	№2
	№3
	Общее количество 2340 + 2340 = выпущенной продукции = 4680 деталей

Вот так результат! Мы сразу же, можно сказать бесплатно, на том же оборудовании увеличили производительность на 1080 деталей, т. е. на целых 30 %.

Нас, однако, продолжает мучить законный вопрос – добились ли мы уже самого лучшего, оптимального решения, или нет? Стоит ли дальше пытаться улучшить план?

В теории математического программирования убедительно показывается, что оптимальному решению соответствует одна из вершин многоугольника допустимых планов, а именно та, для которой общая производительность окажется максимальной. В нашем случае это вершина С.

Действительно, рассчитывая известным уже нам путем план распределения станков для этой точки, получим следующее решение (табл. 7.4).

Таблица 7.4

	Станок	Продолжительность работы станка, мин	Производительность станка (количество деталей за время работы)
	А	Б	А	Б
	№1
	№2
	№3
	Общее количество 2610 + 2610 = выпущенной = 5220 деталей продукции

Мы получили план почти наполовину (на 45 %) лучше, чем глазомерный. И этот существенный прирост, подобно и предыдущему улучшению, ничего (если не считать умственных усилий на планирование) не стоит. Никакого дополнительного расхода каких-либо ресурсов не потребовалось. Те же станки, те же детали, те же станочники работают то же время. Не меняются и производительности станков. Эффект здесь чисто интеллектуальный, «умственный», – за счет рационального распределения ресурсов оборудования (кстати, латинское слово «рационалист» означает «разумный»). Умное, обоснованное решение сделало чудо, в которое даже трудно поверить. Подобный «чудесный» результат, как мы уже понимаем, характерен для всех решений, принимаемых с помощью научных методов.

Может возникнуть, правда, вопрос: а нельзя ли обойтись в подобных задачах без какого-либо специального математического аппарата, идя путем простого перебора всех возможных вариантов решения? Этот соблазн следует тут же отмести. Расчет показывает, что перебор всех возможных вариантов решений подобных задач не под силу даже самому большому коллективу вычислителей.

Уместно отметить еще несколько интересных моментов, связанных с решением данной задачи. Полученный нами оптимальный план – это не просто правильный, допустимый план распределения оборудования, по которому можно работать, – такими были и оба предыдущих. Они обеспечивали как беспростойность оборудования, так и комплектность продукции. Оптимальный план помимо того, что он должен отвечать этим требованиям, должен быть еще обязательно самым эффективным. В данном случае это означает требование максимума деталей. Действительно, как уже отмечалось, оптимизация обязательно должна предусматривать обращение одного из показателей в максимум (или минимум). Но только одного показателя. Нельзя вести оптимизацию по нескольким показателям одновременно. Между тем мы часто слышим: «максимум продукции при минимуме издержек». А правильно будет: «максимум продукции при данном уровне издержек» или «минимум издержек при данном уровне продукции».

И еще один важный вывод, к которому подводит станковая задача: оптимизация возможна лишь по верхнему уровню управления, для всей производственной системы в целом. В данном случае это означает, что мы получили оптимальный план лишь для всех трех станков вместе. А для каждого в отдельности? Тут оптимальности может и не быть. В нашей задаче оптимальный план явно не понравится станочнику, работающему на станке № 3: при большей производительности – 5 деталей в минуту – план предлагает ему работать всего 90 минут, а при меньшей – 3 детали в минуту – целых 270 минут. Но тут уже ничего не поделаешь: чтобы получить оптимальный, сбалансированный план предприятия, кому-то на нижнем уровне приходится работать в неоптимальном режиме. И значительно дешевле компенсировать издержки «внизу», чем лишиться огромного эффекта оптимизации работы целого предприятия.

Несколько слов о существе решения станковой задачи. Идея математического программирования заключается в том, чтобы вместо сплошного (иногда говорят – слепого или дурного) перебора всех возможных вариантов вести перебор выборочный, направленный на скорейшее последовательное улучшение результата. Поэтому в нашей задаче мы и рассматривали не все точки области допустимых планов (их бесчисленное множество), а только вершины многоугольника, одна из которых и дала нам наилучшее решение.

Методы математического программирования находят широкое применение для обоснования оптимальных решений в самых различных областях человеческой деятельности: при планировании перевозок и в торговле, для правильной организации труда, в управлении городским транспортом и строительством.

Рассмотрим, как вырабатываются правила решения еще одной важной производственной задачи.

Дата добавления: 2014-11-16